Derivada de una Constante
La derivada de toda función constante es siempre cero. $$ f(x)=k \:\: \rightarrow \:\: f'(x)=0 $$
Este resultado es inmediato y se puede demostrar con facilidad.
Demostración
Sea f(x) una función definida en el intervalo (a, b), y tomemos un punto cualquiera x de su dominio.
$$ f(x)= k $$
En todo su dominio, la función f(x) devuelve de manera constante el mismo valor k.
La gráfica de una función de este tipo es la siguiente:
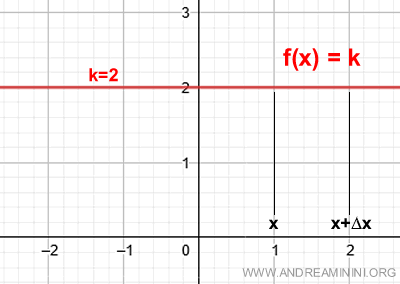
Para calcular la derivada de la función, recurrimos al límite del cociente incremental:
$$ \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} $$
Sabemos que:
- f(x) = k
- f(x + Δx) = k
Por lo tanto, el cociente incremental se reduce a:
$$ \lim_{\Delta x \rightarrow 0} \frac{k - k}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{0}{\Delta x} = 0 $$
De este modo queda demostrado que la derivada de una función constante es, efectivamente, igual a cero.
Un Ejemplo Práctico
Consideremos la función:
$$ f(x) = 2 $$
Calculemos el límite del cociente incremental cuando Δx tiende a cero:
$$ \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} $$
Dado que:
- f(x) = 2
- f(x + Δx) = 2
El límite se simplifica así:
$$ \lim_{\Delta x \rightarrow 0} \frac{2 - 2}{\Delta x} = 0 $$
Por lo tanto, la derivada f'(x) es cero en todos los puntos del dominio de la función.
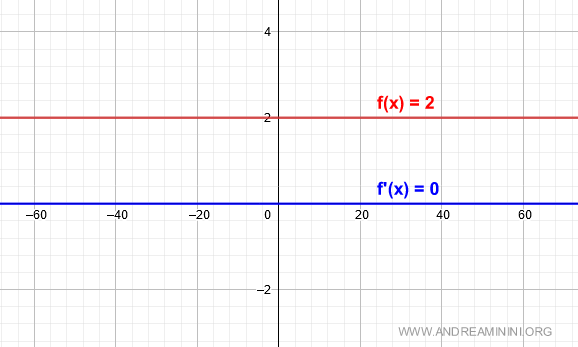
Y con esto queda confirmada la propiedad.