Derivada lateral derecha
Sea una función definida en un intervalo que se prolonga hacia la derecha del punto x0. Decimos que f(x) es diferenciable por la derecha en x0 si existe el límite lateral derecho del cociente incremental entre x y x0, y este límite es finito cuando x tiende a x0 desde la derecha. $$ f'_+(x_0) = \lim_{x \rightarrow x_0^+} \frac{f(x)-f(x_0)}{x - x_0} $$ Como Δx = x - x0, también puede escribirse de la siguiente manera: $$ f'_+(x_0) = \lim_{Δx \rightarrow 0^+} \frac{f(x_0 + Δx) - f(x_0)}{Δx} $$ A esta expresión se la denomina derivada lateral derecha de f(x).
En esta definición solo nos interesan los valores de x situados a la derecha de x0.
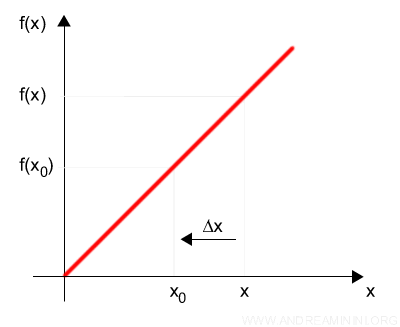
El intervalo a la izquierda de x0 no se considera en este caso.
Nota. En algunos textos se representa el punto x como x0 + δ. Sin embargo, la idea es exactamente la misma: se trata de un punto a la derecha de x0 que se aproxima indefinidamente a x0 al tomar el límite.
Un ejemplo práctico
Comprobemos si existe la derivada lateral derecha de la función f(x) = |x| en el punto x0 = 2.
$$ f(x) = 2 $$
Calculamos el límite cuando x tiende a x0 desde la derecha:
$$ f'_+(x_0) = \lim_{x \rightarrow x_0^+} \frac{f(x) - f(x_0)}{x - x_0} $$
$$ f'_+(2) = \lim_{x \rightarrow 2^+} \frac{f(x) - f(2)}{x - 2} $$
$$ f'_+(2) = \lim_{x \rightarrow 2^+} \frac{|x| - |2|}{x - 2} $$
Dado que x se mantiene positivo en este límite, resulta:
$$ f'_+(2) = \lim_{x \rightarrow 2^+} \frac{x - 2}{x - 2} = +1 $$
Por lo tanto, la derivada lateral derecha de f(x) en x0 = 2 es igual a +1.
Así es como se llega al resultado.