Máximos y mínimos mediante derivadas

Los valores máximos y mínimos de una función f(x) pueden determinarse analizando sus derivadas.

Si la primera derivada se anula en x₀: $$ f'(x_0) = 0 $$ entonces la función presenta:
• un máximo local si la segunda derivada es negativa $$ f''(x_0) < 0 $$
• un mínimo local si la segunda derivada es positiva $$ f''(x_0) > 0 $$

Criterio general

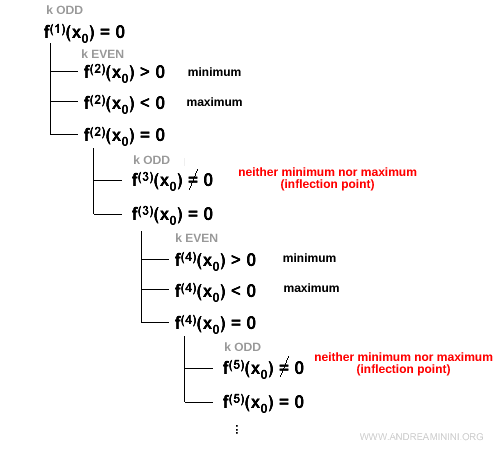
Este criterio para identificar mínimos y máximos puede generalizarse de la siguiente forma:

Si la k-ésima derivada se anula en x₀ y k es impar:

$$ f^{(k)}(x_0) = 0 \quad \text{con} \quad k \text{ impar} $$

Entonces la función tiene:

• un máximo local si la derivada (k+1)-ésima es negativa $$ f^{(k+1)}(x_0) < 0 $$
• un mínimo local si la derivada (k+1)-ésima es positiva $$ f^{(k+1)}(x_0) > 0 $$
• ni máximo ni mínimo si la derivada (k+1)-ésima es cero mientras que la derivada (k+2)-ésima es distinta de cero $$ f^{(k+1)}(x_0) = 0 \:\: \text{y} \:\: f^{(k+2)}(x_0) \ne 0 $$ En este caso, la función presenta un punto de inflexión.

Nota. Si la k-ésima derivada se anula y k es par, la función no presenta ni mínimo ni máximo en x₀, siempre que la derivada (k+1)-ésima sea distinta de cero. En tales casos, se trata de un punto de inflexión.

Demostración

Para justificar este criterio, partimos del desarrollo en serie de Taylor de una función continua y derivable hasta orden n en x₀:

$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$

que puede escribirse también como:

$$ f(x) = f(x_0) + f^{(1)}(x_0) \cdot \frac{ (x - x_0)^1 }{1!} + f^{(2)}(x_0) \cdot \frac{ (x - x_0)^2 }{2!} + \dots + f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n!} + R_n $$

Supongamos que todas las derivadas hasta el orden n - 1 se anulan en x₀:

$$ f'(x_0) = f''(x_0) = f^{(3)}(x_0) = \dots = f^{(n-1)}(x_0) = 0 $$

En esas condiciones, el desarrollo de Taylor se simplifica a:

$$ f(x) = f(x_0) + f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n!} + R_n $$

Si la derivada n-ésima es positiva en x₀:

$$ f^{(n)}(x_0) > 0 $$

Nota. El razonamiento es análogo si f⁽ⁿ⁾ fuera negativa en x₀: en ese caso el punto correspondería a un máximo local en lugar de a un mínimo.

Consideremos ahora el límite:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{(x - x_0)^n} $$

Sustituyendo según el desarrollo de Taylor reducido:

$$ \lim_{x \rightarrow x_0} \frac{\left[ f(x_0) + f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n! } + R_n \right] - f(x_0)}{(x - x_0)^n} $$

$$ \lim_{x \rightarrow x_0} \frac{ f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n! } + R_n }{(x - x_0)^n} $$

$$ \lim_{x \rightarrow x_0} \left[ f^{(n)}(x_0) \cdot \frac{ (x - x_0)^n }{n! } + R_n \right] \cdot \frac{1}{(x - x_0)^n} $$

$$ \lim_{x \rightarrow x_0} \frac{ f^{(n)}(x_0) }{n! } + \frac{R_n}{(x - x_0)^n} = \frac{ f^{(n)}(x_0) }{n! } > 0 $$

Por lo tanto, el límite resulta estrictamente positivo:

$$ \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{(x - x_0)^n} > 0 $$

En este punto distinguimos dos situaciones según n sea par o impar:

• Si n es par, el denominador (x - x₀)ⁿ siempre es positivo, lo que implica que f(x) > f(x₀) en cualquier entorno de x₀. En consecuencia, x₀ es un mínimo local.
• Si n es impar, el denominador (x - x₀)ⁿ cambia de signo a un lado y otro de x₀. Por lo tanto, x₀ no puede ser un mínimo local.

En conclusión, x₀ es un mínimo local únicamente si f⁽ⁿ⁾ ≠ 0 y n es par.

Ejemplo práctico

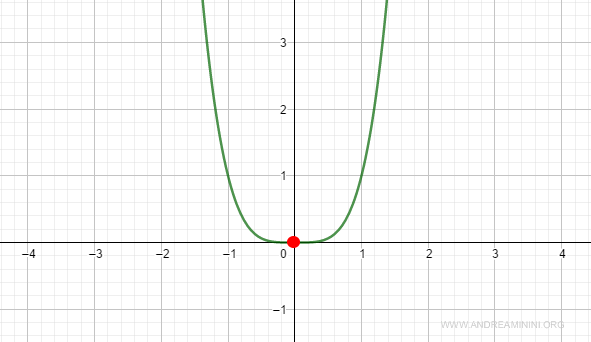
Ejemplo 1 (n par)

Consideremos la función:

$$ f(x) = x^4 $$

En x₀ = 0, la primera, segunda y tercera derivada se anulan:

$$ f^{(1)}(x_0) = 4x^3 = 4(0)^3 = 0 $$

$$ f^{(2)}(x_0) = 12x^2 = 12(0)^2 = 0 $$

$$ f^{(3)}(x_0) = 24x = 24(0) = 0 $$

La cuarta derivada, al ser de orden par, es positiva en x₀:

$$ f^{(4)}(x_0) = 24 > 0 $$

Por lo tanto, la función tiene un mínimo local en x₀.

Ejemplo 2 (n impar)

Consideremos la función:

$$ f(x) = x^3 $$

En x₀ = 0, la primera y segunda derivada se anulan:

$$ f^{(1)}(x_0) = 3x^2 = 3(0)^2 = 0 $$

$$ f^{(2)}(x_0) = 6x = 6(0) = 0 $$

La tercera derivada, que es de orden impar, resulta positiva:

$$ f^{(3)}(x_0) = 6 > 0 $$

En este caso es evidente que el punto no corresponde a un mínimo local.

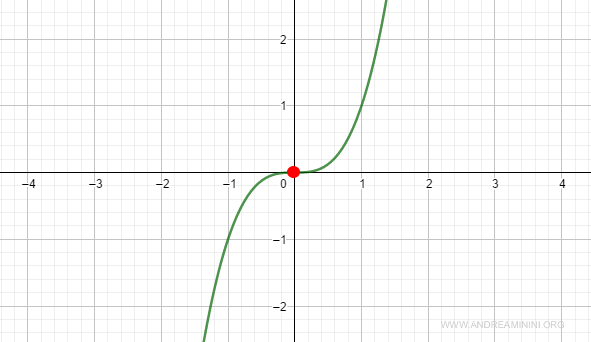
En x₀, la función presenta un punto de inflexión.

Y así sucesivamente.