Funciones crecientes y decrecientes
Sea \( y = f(x) \) una función con dominio \( D \subseteq \mathbb{R} \). Consideremos un intervalo \( I \) contenido en \( D \). Dados dos valores cualesquiera \( x_1 \) y \( x_2 \) pertenecientes a \( I \), con \( x_1 < x_2 \), se dice que la función es:
- estrictamente creciente, si \( f(x_1) < f(x_2) \)
- creciente (o no decreciente), si \( f(x_1) \le f(x_2) \)
- estrictamente decreciente, si \( f(x_1) > f(x_2) \)
- decreciente (o no creciente), si \( f(x_1) \ge f(x_2) \)
Cuando una función mantiene el mismo comportamiento en todo un intervalo, es decir, es siempre creciente o siempre decreciente, se dice que es monótona en el intervalo \( I \).
La monotonía describe cómo se relacionan los valores de la función a medida que aumenta la variable independiente. No se refiere a la forma visual de la gráfica, sino a la comparación ordenada entre los valores que toma la función.
Ejemplo. En la figura, la función f(x) es estrictamente creciente en el intervalo $ ( x_1,x_2) $ y estrictamente decreciente en el intervalo $ ( x_3 , x_4) $
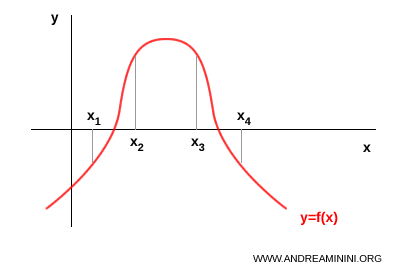
Criterio de monotonía de una función
Funciones crecientes y decrecientes
Para determinar si una función es creciente o decreciente, utilizamos el criterio de monotonía, que establece la relación entre la primera derivada de una función \( f(x) \) y su comportamiento de crecimiento o decrecimiento.
Función creciente
Una función \( f(x) \), continua en [a, b] y derivable en (a, b), se dice creciente en [a, b] si su primera derivada cumple $$ f'(x) \ge 0 $$ para todo \( x \in (a, b) \).
Función decreciente
Una función \( f(x) \), continua en [a, b] y derivable en (a, b), se dice decreciente en [a, b] si su primera derivada satisface $$ f'(x) \le 0 $$ para todo \( x \in (a, b) \).
¿Por qué es relevante?
El signo de la primera derivada \( f'(x) \) constituye una herramienta esencial en el análisis y en la representación gráfica de una función.
Ejemplo práctico
Consideremos la función:
$$ f(x)=x^2 $$
Su primera derivada es:
$$ f'(x)=2x $$
En el intervalo \((-\infty,0)\), la derivada \( f'(x)=2x \) es negativa, mientras que en \((0,+\infty)\) resulta positiva:
$$ f'(x)= \begin{cases} 2x > 0 \quad \text{si } x > 0 \\ 2x < 0 \quad \text{si } x < 0 \end{cases} $$
Por lo tanto, la función \( f(x)=x^2 \) es decreciente en \((-\infty, 0)\) y creciente en \((0, \infty)\).
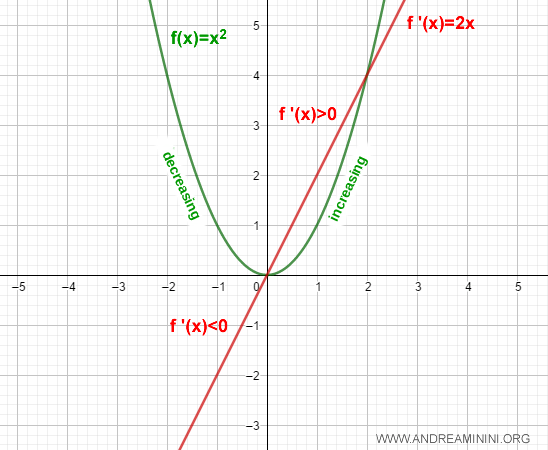
Demostración y explicación
Caso 1 (Primera derivada no negativa)
Supongamos que la primera derivada \( f'(x) \) es no negativa en el intervalo (a, b):
$$ f'(x) \ge 0 $$
Queremos verificar que, bajo esta condición, la función sea efectivamente creciente.
Tomemos dos puntos \( x1 \) y \( x2 \) en (a, b) tales que:
$$ a \le x_1 \le x_2 \le b $$
Si la función es creciente, debe cumplirse:
$$ f(a) \le f(x_1) \le f(x_2) \le f(b) $$
De acuerdo con el teorema del valor medio de Lagrange, existe un punto \( x0 \in (x_1, x_2) \) tal que:
$$ f'(x_0)=\frac{f(x_2)-f(x_1)}{x_2 - x_1} $$
Reordenando:
$$ f(x_2)-f(x_1) = f'(x_0)\,(x_2 - x_1) $$
Dado que \( f'(x_0) \ge 0 \) por hipótesis y que \( (x_2 - x_1) > 0 \), se concluye que:
$$ f(x_2)-f(x_1) \ge 0 $$
En consecuencia, la función es creciente en el intervalo (x1, x2).
Esto establece el vínculo entre una primera derivada no negativa y el carácter creciente de la función.
Nota. De manera análoga, si la primera derivada es no positiva \( f'(x) \le 0 \), se deduce que la función es decreciente, ya que \( (x_2 - x_1) > 0 \) implica necesariamente \( f(x_2) - f(x_1) \le 0 \).
Caso 2 (Función creciente)
Supongamos ahora que la función es creciente en el intervalo (a, b), sin haber considerado aún su derivada.
Esto significa que para cualquier punto \( x_0 \in (a, b) \), la función aumenta en su entorno.
Para calcular la derivada en \( x_0 \), evaluamos el límite del cociente incremental en ese punto:
$$ f'(x_0) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$
Dado que la función es creciente, el numerador del cociente incremental cumple:
- \( f(x+h) - f(x) \ge 0 \) si \( h > 0 \)
- \( f(x+h) - f(x) \le 0 \) si \( h < 0 \)
De este modo, el cociente incremental resulta no negativo para \( h > 0 \) (derivada lateral derecha):
$$ f'(x_0+) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$
y también no negativo para \( h < 0 \) (derivada lateral izquierda):
$$ f'(x_0-) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \ge 0 $$
Nota. En el caso de la derivada lateral izquierda, el denominador \( h \) es negativo (\( h < 0 \)). Como el numerador \( f(x+h)-f(x) \) es también no positivo, el cociente permanece no negativo.
Por lo tanto, la primera derivada de la función en \( x_0 \) resulta no negativa:
$$ f'(x_0) \ge 0 $$
Y así sucesivamente.