Fórmula de Taylor
La fórmula de Taylor permite aproximar una función f(x), n veces derivable en un entorno de un punto x0 ∈ ℝ, mediante un polinomio de grado n acompañado de un término de resto R. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x-x_0)^k + R_n(x) $$ donde $$ \lim_{x \rightarrow x_0} \frac{R_n}{(x-x_0)^n} = 0 $$
A este polinomio se le denomina Polinomio de Taylor de f(x) en x0, de grado (u orden) n.
Cuanto mayor sea el grado n, con mayor exactitud el polinomio aproxima la función.
Cuando n tiende a infinito, el término de resto R converge a cero:
$$ \lim_{n \rightarrow \infty} R_n = 0 $$
¿Por qué es útil? La fórmula de Taylor nos brinda la posibilidad de expresar una función f(x) en forma de un polinomio algebraico P(x). Esta representación suele facilitar notablemente el estudio de sus propiedades y su comportamiento.
Un ejemplo práctico
Consideremos la función exponencial:
$$ f(x) = e^x $$
La expandimos alrededor del punto x0 = 0:
$$ x_0 = 0 $$
En dicho punto, la función toma el valor:
$$ f(0) = e^0 = 1 $$
Dado que todas las derivadas de ex coinciden con la propia función, se cumple que:
$$ D[e^x] = e^x $$
Por consiguiente, para cualquier entero k:
$$ f^{(k)}(0) = 1 $$
Así, el polinomio de Taylor de grado n = 2 resulta ser:
$$ f(x) = \frac{f^{(0)}(x_0)}{0!} \cdot (x - x_0)^0 + \frac{f^{(1)}(x_0)}{1!} \cdot (x - x_0)^1 + \frac{f^{(2)}(x_0)}{2!} \cdot (x - x_0)^2 + R_2 $$
$$ f(x) = \frac{D^{(0)}[e(x_0)]}{0!} \cdot (x - x_0)^0 + \frac{D^{(1)}[e(x_0)]}{1!} \cdot (x - x_0)^1 + \frac{D^{(2)}[e(x_0)]}{2!} \cdot (x - x_0)^2 + R_2 $$
Recordando que la derivada de orden cero es simplemente la propia función, obtenemos:
$$ f(x) = \frac{e(x_0)}{0!} \cdot (x - x_0)^0 + \frac{D^{(1)}[e(x_0)]}{1!} \cdot (x - x_0)^1 + \frac{D^{(2)}[e(x_0)]}{2!} \cdot (x - x_0)^2 + R_2 $$
Al sustituir x0 = 0 se sigue que:
$$ f(x) = \frac{e(0)}{0!} \cdot (x - 0)^0 + \frac{D^{(1)}[e(0)]}{1!} \cdot (x - 0)^1 + \frac{D^{(2)}[e(0)]}{2!} \cdot (x - 0)^2 + R_2 $$
$$ f(x) = \frac{e(0)}{0!} \cdot x^0 + \frac{D^{(1)}[e(0)]}{1!} \cdot x^1 + \frac{D^{(2)}[e(0)]}{2!} \cdot x^2 + R_2 $$
Como toda derivada k-ésima de ex sigue siendo ex, se obtiene:
$$ f(x) = \frac{e(0)}{0!} \cdot x^0 + \frac{e(0)}{1!} \cdot x^1 + \frac{e(0)}{2!} \cdot x^2 + R_2 $$
Y dado que e0 = 1:
$$ f(x) = \frac{1}{0!} \cdot x^0 + \frac{1}{1!} \cdot x^1 + \frac{1}{2!} \cdot x^2 + R_2 $$
Al evaluar los factoriales de los denominadores (con 0! definido como 1) llegamos a:
$$ f(x) = \frac{1}{1} \cdot x^0 + \frac{1}{1} \cdot x^1 + \frac{1}{2} \cdot x^2 + R_2 $$
$$ f(x) = \frac{x^0}{1} + \frac{x^1}{1} + \frac{x^2}{2} + R_2 $$
$$ f(x) = 1 + x + \frac{x^2}{2} + R_2 $$
Aun siendo un polinomio de grado 2, esta aproximación ya resulta bastante fiel a la función f(x) = ex.
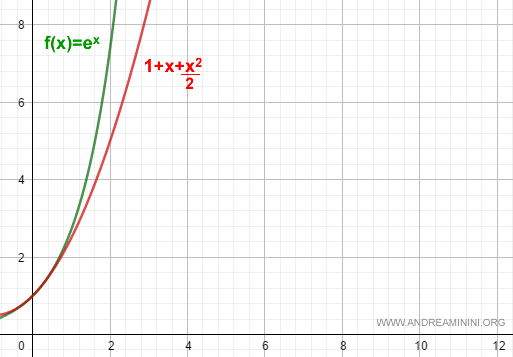
Si incrementamos el grado del polinomio a k + 1 = 3, la aproximación se afina todavía más:
$$ f(x) = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + R_3 $$
Este nuevo polinomio de tercer grado se ajusta a la gráfica de la función con mayor precisión que el anterior de segundo grado (representado con línea discontinua).
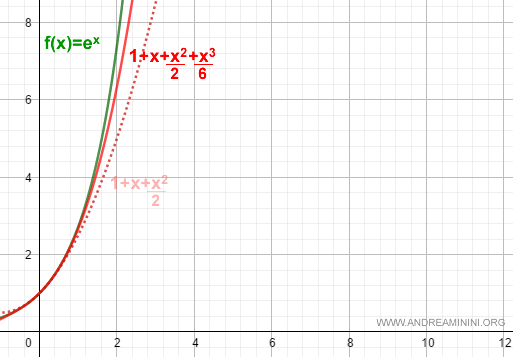
De este modo, el término de resto del polinomio de Taylor tiende a cero a medida que k crece indefinidamente:
$$ \lim_{k \rightarrow \infty} R_k = 0 $$
Demostración
Supongamos que la derivada n-ésima f(n)(x) es continua en x0.
Queremos probar que el término de resto en la fórmula de Taylor se anula en el límite cuando x tiende a x0:
$$ \lim_{x \rightarrow x_0} \frac{R_n}{(x - x_0)^n} = 0 $$
Por definición, el resto R es la diferencia entre la función f(x) y su polinomio de Taylor:
$$ R_n = f(x) - P(x) $$
$$ R_n = f(x) - \left[ f(x_0) + f'(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^n}{n!} \right] $$
Al sustituir R en el límite resulta:
$$ \lim_{x \rightarrow x_0} \frac{f(x) - \left[ f(x_0) + f'(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^n}{n!} \right]}{(x - x_0)^n} = \frac{0}{0} $$
Nota. El numerador se anula porque f(x) y su polinomio de Taylor coinciden exactamente en x0. El denominador, por su parte, tiende a cero cuando x se aproxima a x0. De ahí que el límite adopte la forma indeterminada 0/0.
Para resolver esta indeterminación aplicamos el Teorema de L’Hôpital.
Derivamos numerador y denominador respecto de x:
$$ \lim_{x \rightarrow x_0} \frac{D \left[ f(x) - \left( f(x_0) + f'(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^n}{n!} \right) \right]}{D \left[ (x - x_0)^n \right]} $$
$$ \lim_{x \rightarrow x_0} \frac{ f'(x) - \left[ f'(x_0) + f''(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^{n - 1}}{(n - 1)!} \right] }{ n \cdot (x - x_0)^{n - 1} } = \frac{0}{0} $$
Como sigue siendo una indeterminación, aplicamos repetidamente el Teorema de L’Hôpital, derivando numerador y denominador un total de n veces.
Tras efectuar n derivadas obtenemos:
$$ \lim_{x \rightarrow x_0} \frac{f^{(n)}(x) - f^{(n)}(x_0)}{n!} $$
Dado que f(x) es continua en x0, el numerador tiende a cero cuando x → x0, ya que f^{(n)}(x) - f^{(n)}(x_0) → 0.
El denominador es la constante n!, es decir, el factorial del grado del polinomio.
Por lo tanto, el límite resulta ser cero:
$$ \lim_{x \rightarrow x_0} \frac{f^{(n)}(x) - f^{(n)}(x_0)}{n!} = 0 $$
De aquí se concluye que el límite original también es nulo:
$$ \lim_{x \rightarrow x_0} \frac{ f'(x) - \left[ f'(x_0) + f''(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^{n - 1}}{(n - 1)!} \right] }{ n \cdot (x - x_0)^{n - 1} } = 0 $$
lo que demuestra que:
$$ \lim_{x \rightarrow x_0} \frac{R_n}{(x - x_0)^n} = 0 $$
Con ello queda establecida la validez de la fórmula de Taylor.
Resto de Peano
El resto de Peano se define como la diferencia entre el polinomio de Taylor pn, de grado n y centrado en x0, y la función f(x) que se desea aproximar: $$ R_n(x) = f(x) - p_n(x) $$
Este resto cuantifica el error que se comete al aproximar f(x) mediante su polinomio de Taylor:
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$
El polinomio de Taylor pn(x) viene dado por:
$$ p_n(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k $$
De manera inmediata, se obtiene la identidad fundamental:
$$ f(x) = p_n(x) + R_n(x) $$
$$ f(x) - p_n(x) = R_n(x) $$
Por lo tanto, el resto de Peano R expresa con exactitud la diferencia entre la función f(x) y su polinomio de Taylor pn(x), de grado n y centrado en x0.
Decimos que el resto de Peano Rn(x) es de orden superior a (x - x0)n cuando f(x) es n veces derivable en x0: $$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x - x_0)^n} = 0 $$
Demostración
$$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x - x_0)^n} $$
Dado que Rn(x) = f(x) - pn(x):
$$ \lim_{x \rightarrow x_0} \frac{f(x) - p_n(x)}{(x - x_0)^n} $$
Sustituimos pn(x) por su desarrollo de Taylor:
$$ \lim_{x \rightarrow x_0} \frac{f(x) - \left[ f(x_0) + f'(x_0)(x - x_0) + \dots + \frac{f^{(n)}(x_0)(x - x_0)^n}{n!} \right]}{(x - x_0)^n} $$
Este límite presenta de nuevo una indeterminación del tipo 0/0.
Para resolverla, aplicamos el Teorema de L’Hôpital de forma iterada (n - 1 veces):
$$ \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - \left[ f^{(n-1)}(x_0) + f^{(n)}(x_0)(x - x_0) \right]}{n! \cdot (x - x_0)} $$
Extraemos el factor 1/n! del límite:
$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - \left[ f^{(n-1)}(x_0) + f^{(n)}(x_0)(x - x_0) \right]}{(x - x_0)} $$
$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0) - f^{(n)}(x_0)(x - x_0)}{(x - x_0)} $$
Reordenando los términos:
$$ \frac{1}{n!} \lim_{x \rightarrow x_0} \left[ \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0)}{(x - x_0)} - f^{(n)}(x_0) \right] $$
Podemos descomponer el límite en dos partes:
$$ \frac{1}{n!} \left[ \lim_{x \rightarrow x_0} \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0)}{(x - x_0)} - \lim_{x \rightarrow x_0} f^{(n)}(x_0) \right] $$
Aplicando de nuevo el Teorema de L’Hôpital al primer término obtenemos f(n)(x):
$$ \frac{1}{n!} \cdot \left[ f^{(n)}(x_0) - f^{(n)}(x_0) \right] $$
$$ \frac{1}{n!} \cdot 0 $$
$$ = 0 $$
Nota. El resto de Peano Rn(x) es un infinitésimo de orden superior respecto de (x - x0)n: $$ \lim_{x \rightarrow x_0} \frac{R_n(x)}{(x - x_0)^n} = 0 $$ En consecuencia, en el polinomio de Taylor puede expresarse mediante la notación de “o pequeña”: $$ R_n(x) = o\bigl((x - x_0)^n\bigr) $$ lo que nos permite escribir: $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + o\bigl((x - x_0)^n\bigr) $$
Fórmula de Taylor en notación alternativa
Si el resto de Peano es de orden o((x - x0)n), la fórmula de Taylor puede expresarse también en la siguiente forma equivalente:
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + o\bigl((x - x_0)^n\bigr) $$
Estimación del resto de Peano
Si f(x) es (n+1) veces derivable en un entorno de x0, su derivada de orden (n+1) es continua, y M representa el valor máximo de esa derivada en dicho entorno, entonces se cumple la siguiente estimación para el resto de Peano: $$ |R_n(x)| \le M \cdot \frac{|x - x_0|^{n+1}}{(n+1)!} $$
Fórmula de Maclaurin
La fórmula de Maclaurin constituye un caso particular de la de Taylor, correspondiente al centro x0 = 0: $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o\bigl(x^n\bigr) $$
Y así sucesivamente.