Serie de Maclaurin
La serie de Maclaurin (a veces escrita McLaurin) es una herramienta que permite aproximar el comportamiento de una función en torno al punto x0 = 0. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o(x^n) $$
El polinomio obtenido constituye una aproximación de orden n de la función f(x) alrededor del origen.
Cuanto mayor sea el grado n del polinomio de Maclaurin, más precisa será la aproximación de f(x) en las cercanías de cero.
Nota. La serie de Maclaurin no es más que un caso particular de la serie de Taylor, cuando x0 = 0. $$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$
Un ejemplo práctico
Consideremos la función exponencial:
$$ f(x) = e^x $$
Su gráfica es la siguiente:
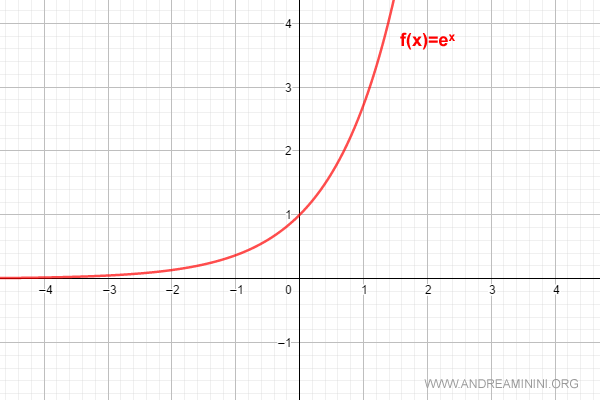
Queremos construir un polinomio que aproxime la función exponencial mediante la serie de Maclaurin:
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!} \cdot x^k + o(x^n) $$
o, de manera equivalente:
$$ P_n(x) = \sum_{k=0}^{n} \frac{D^{(k)}[e^0]}{k!} \cdot x^k + o(x^n) $$
Para n = 0, la serie se reduce a:
$$ P_0(x) = \sum_{k=0}^{0} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 $$
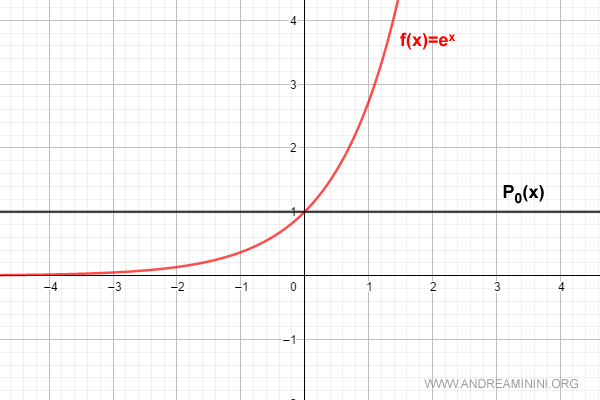
Para n = 1 obtenemos:
$$ f(x) = \sum_{k=0}^{1} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x $$
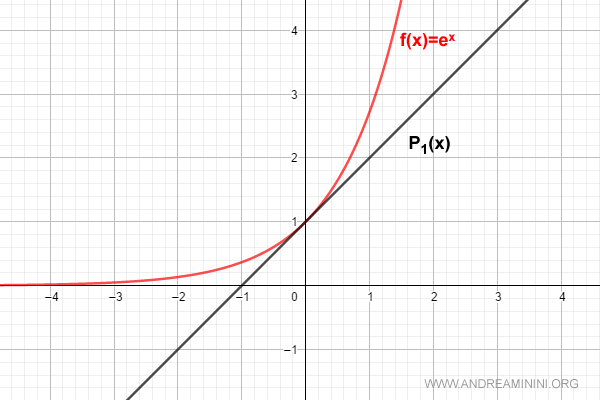
Para n = 2, la aproximación es:
$$ f(x) = \sum_{k=0}^{2} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} $$
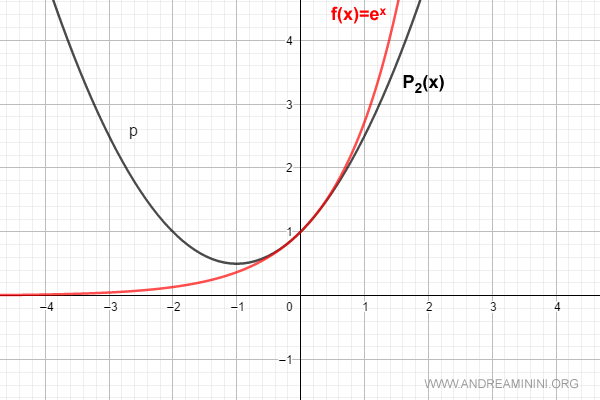
Para n = 3, resulta:
$$ f(x) = \sum_{k=0}^{3} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} $$
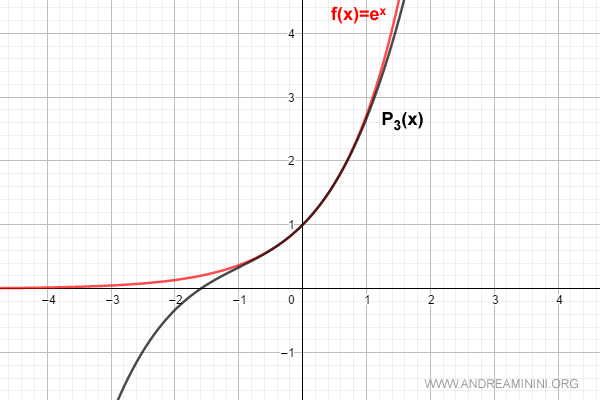
A medida que aumenta el grado del polinomio, la serie de Maclaurin proporciona una aproximación progresivamente más exacta de la función en torno a x0 = 0.
Por ejemplo, con n = 9, el polinomio aproxima la función con gran precisión en un entorno próximo al cero:
$$ f(x) = \sum_{k=0}^{9} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots + \frac{x^9}{9!} $$
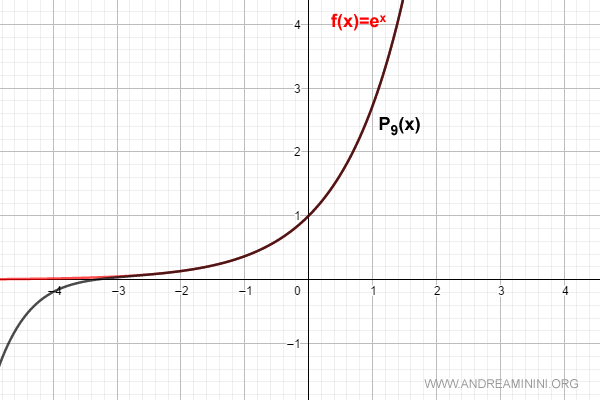
En general, para cualquier entero positivo n, el polinomio adopta la forma:
$$ f(x) = \sum_{k=0}^{n} \frac{D^{(k)}[e^0]}{k!} \cdot x^k = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots + \frac{x^n}{n!} $$
Y así sucesivamente.