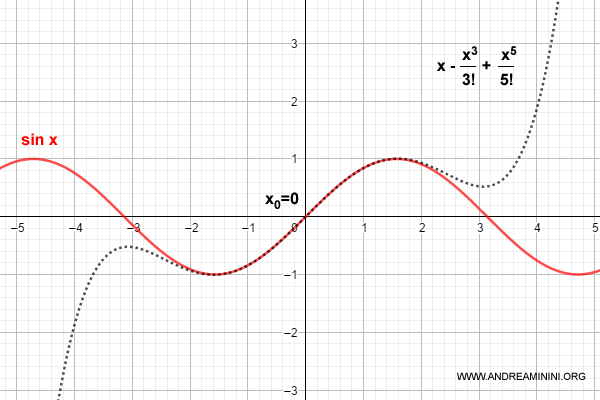
Cómo Aproximar la Función Seno mediante el Polinomio de Taylor o de Maclaurin
En este ejercicio se busca aproximar la función seno utilizando un polinomio de Taylor.
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(x_0)}{k!} \cdot (x - x_0)^k + R_n(x) $$
Tomamos como centro x0 = 0, lo que simplifica el desarrollo a la serie de Maclaurin, y consideramos el polinomio de grado n = 5.
Nota. La serie de Maclaurin es un caso particular del polinomio de Taylor con centro en x0 = 0. En muchos problemas resulta más conveniente trabajar en este marco, ya que los cálculos se simplifican considerablemente.
Para construir el polinomio calculamos término a término la serie de Taylor, desde n = 0 hasta n = 5, y finalmente añadimos el resto de Peano.
Grado n = 0
$$ \frac{D^{0} \sin 0 }{0!} \cdot (x - 0)^0 = \frac{\sin 0}{1} \cdot 1 = 0 $$
El primer término de la serie es cero.
Grado n = 1
$$ \frac{D^{1} \sin 0 }{1!} \cdot (x - 0)^1 = \frac{\cos 0}{1} \cdot x = x $$
El segundo término es x.
Grado n = 2
$$ \frac{D^{2} \sin 0 }{2!} \cdot (x - 0)^2 = \frac{-\sin 0}{2!} \cdot x^2 = 0 $$
El tercer término es cero.
Grado n = 3
$$ \frac{D^{3} \sin 0 }{3!} \cdot (x - 0)^3 = \frac{-\cos 0}{3!} \cdot x^3 = \frac{-1}{3!} \, x^3 $$
El cuarto término es -x3/3!.
Nota. En la práctica basta con derivar sucesivamente, sin recalcular desde cero. Así, de $-\sin(0)$ se obtiene inmediatamente la tercera derivada $-\cos(0)$.
Grado n = 4
$$ \frac{D^{4} \sin 0 }{4!} \cdot (x - 0)^4 = \frac{\sin 0}{4!} \cdot x^4 = 0 $$
El quinto término es cero.
Grado n = 5
$$ \frac{D^{5} \sin 0 }{5!} \cdot (x - 0)^5 = \frac{\cos 0}{5!} \cdot x^5 = \frac{1}{5!} \, x^5 $$
El sexto término es x5/5!.
De este modo hemos obtenido todos los términos del polinomio de Taylor hasta grado 5. Falta únicamente el resto.
Resto de Peano
Se expresa con la notación o minúscula:
$$ R_n = o((x - x_0)^n) $$
Con x0 = 0 y n = 5:
$$ R_5 = o(x^5) $$
Nota. La notación $o(x^n)$ indica que el resto es de orden estrictamente superior a $x^n$, es decir, tiende a cero más rápido que $x^n$ cuando $x \to x_0$: $$ \lim_{x \rightarrow x_0} \frac{R_n}{(x - x_0)^n} = 0 $$
Podemos ahora escribir el polinomio completo:
$$ p_5 = x - \frac{x^3}{3!} + \frac{x^5}{5!} + o(x^5) $$
Nota. Al haber tomado x0 = 0, se trata en realidad de un polinomio de Maclaurin. El mismo procedimiento vale para cualquier centro distinto de cero.
El polinomio de quinto grado aproxima bien a la función seno en las cercanías de x = 0.
Generalización para un n Arbitrario
Podemos generalizar el desarrollo para cualquier entero n. Al observar la serie completa, incluidos los términos nulos, se identifican dos pautas claras:
$$ 0 + x + 0 - \frac{x^3}{3!} + 0 + \frac{x^5}{5!} + \dots $$
- Solo aparecen términos de grado impar (n = 1, 3, 5...), mientras que los de grado par se anulan.
Nota. El término inicial corresponde a n = 0; por eso, n = 1 se considera ya el segundo término.
- Los coeficientes de los términos impares alternan de signo.
Los exponentes impares se generan con la expresión 2n + 1:
$$ x - \frac{x^3}{3!} + \frac{x^5}{5!} + \dots $$
Para introducir la alternancia de signos, basta multiplicar cada término por $(-1)^n$.
Así, la serie de Taylor/Maclaurin general para el seno queda:
$$ p_n = \sum_{k=0}^{n} (-1)^k \, \frac{x^{2k+1}}{(2k+1)!} + o(x^{2n+1}) $$
Además, dado que los términos pares son nulos, se cumple que:
$$ P_{2n+1} = P_{2n+2} $$
y por ello el resto puede expresarse de forma más precisa como $o(x^{2n+2})$.
En conclusión, la serie de Taylor/Maclaurin del seno para cualquier entero n es:
$$ p_n = \sum_{k=0}^{n} (-1)^k \, \frac{x^{2k+1}}{(2k+1)!} + o(x^{2n+2}) $$
Con esto queda establecida la expansión de la función seno mediante series de Taylor/Maclaurin para todo n.