Infinitésimos en Matemáticas
¿Qué es un infinitésimo?
En matemáticas, un infinitésimo es una cantidad tan pequeña que se considera menor que cualquier número real positivo, aunque nunca sea exactamente cero. La noción de infinitésimo fue introducida por Leibniz y constituye una idea fundamental en el cálculo. Con frecuencia también se designa mediante la notación de “o pequeño”.
La función infinitesimal
Una función se denomina función infinitesimal en $x0$ si el límite de $f(x)$ tiende a cero cuando $x$ se aproxima a $x0$:
$$ \lim_{x \rightarrow x_0} f(x) = 0 $$
En muchos contextos, la palabra infinitésimo se emplea de manera informal para aludir directamente a una función de este tipo.
Ejemplo
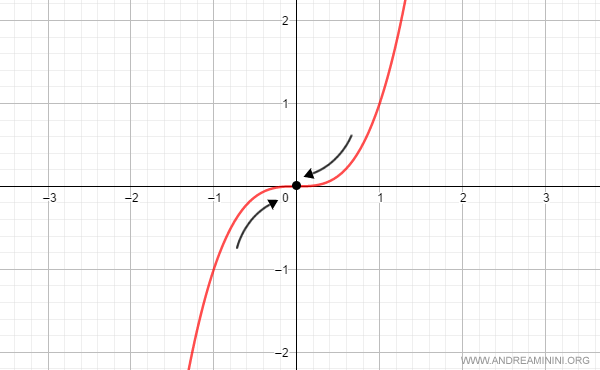
La siguiente función es infinitesimal cuando $x$ tiende a cero:
$$ f(x) = x^3 $$
Aunque $f(x)$ nunca es exactamente nula en ningún entorno de $x0$,
su límite al acercarse $x$ a $x0$ resulta ser cero:
$$ \lim_{x \rightarrow 0} x^3 = 0 $$
Por lo tanto, $f(x)$ es una función infinitesimal en torno a $x=0$.
Infinitésimos de orden superior
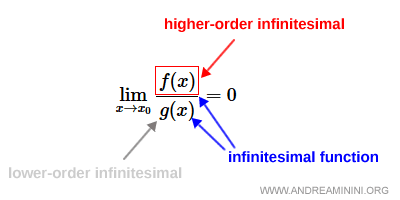
Sean $f(x)$ y $g(x)$ dos funciones definidas en un entorno de $x0$ (posiblemente excluyendo el propio $x0$), y distintas de cero para $x \ne x0$. Decimos que $f(x)$ es un infinitésimo de orden superior respecto de $g(x)$ cuando $x$ tiende a $x0$ si se cumple:
$$ \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = 0 $$
Al igual que las funciones infinitas pueden jerarquizarse por su velocidad de crecimiento, las funciones infinitesimales pueden compararse según la rapidez con la que se anulan.
Si tanto $f(x)$ como $g(x)$ tienden a cero cuando $x \rarr x0$, se dice que es de orden superior aquella función que se aproxima al cero con mayor rapidez.
A la inversa, $g(x)$ se denomina infinitésimo de orden inferior en comparación con $f(x)$ cuando $x \rarr x0$.
En este caso, el límite del cociente $g(x)/f(x)$ diverge hacia el infinito:
$$ \lim_{x \rightarrow x_0} \frac{g(x)}{f(x)} = \infty $$
Nota: El orden de los infinitésimos solo puede establecerse cuando las funciones que tienden a cero cerca de $x \rarr x0$ son comparables. Si el límite del cociente $f(x)/g(x)$ existe y es un número real distinto de cero, se dice que ambas funciones son infinitésimos del mismo orden:
$$ \lim_{x \rightarrow x_0} \frac{g(x)}{f(x)} = l $$
Los infinitésimos de orden superior están estrechamente relacionados con la notación matemática conocida como o pequeño.
Ejemplo
Consideremos dos funciones infinitesimales cuando $x$ tiende a cero:
$$ f(x) = x^3 $$
$$ g(x) = x^2 $$
Ambas funciones se anulan al acercarse $x$ a cero:
$$ \lim_{x \rightarrow 0} x^3 = 0 $$
$$ \lim_{x \rightarrow 0} x^2 = 0 $$
No obstante, pertenecen a órdenes distintos de pequeñez.
Esto se observa claramente en sus gráficas:
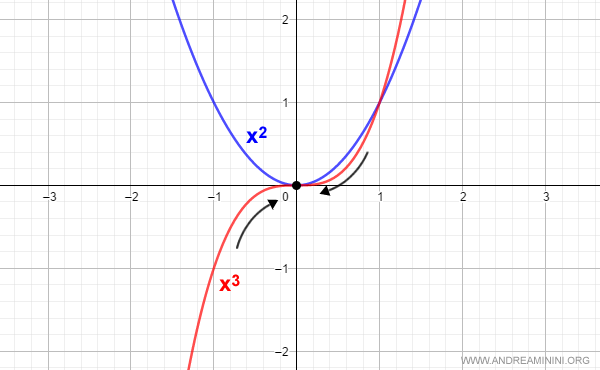
Nota: En las proximidades de $x0 = 0$, la función $f(x) = x^3$ (curva roja) se acerca mucho más al eje x (es decir, al valor cero) que $g(x) = x^2$ (curva azul).
Como $f(x)$ tiende a cero más rápidamente que $g(x)$ cuando $x \rarr 0$, el cociente $f(x)/g(x)$ también tiende a cero al aproximarse $x$ a cero:
$$ \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = \lim_{x \rightarrow x_0} \frac{x^3}{x^2} = \lim_{x \rightarrow x_0} x = 0 $$
En consecuencia, $f(x)$ es un infinitésimo de orden superior en relación con $g(x)$ cuando $x \rarr 0$.
El significado de "o pequeño"
Si $f(x)$ es un infinitésimo de orden superior con respecto a $g(x)$ cuando $x \rarr x0$, esta relación puede expresarse también mediante la notación de o pequeño:
$$ f(x) = o(g(x)) \:\:\: \text{cuando} \: x \rightarrow x_0 $$
Ejemplo
Tomemos nuevamente dos funciones infinitesimales cuando $x$ tiende a cero:
$$ f(x) = x^3 $$
$$ g(x) = x^2 $$
Dado que $f(x)$ es un infinitésimo de orden superior en comparación con $g(x)$ cuando $x$ se aproxima a cero:
$$ \lim_{x \rightarrow x_0} \frac{f(x)}{g(x)} = 0 $$
Podemos escribir esta relación utilizando la notación de o pequeño:
$$ f(x) = o(g(x)) \:\:\: \text{cuando} \: x \rightarrow x_0 $$
En otras palabras, se dice que $f(x)$ es “o pequeño de $g(x)$”.
Y así sucesivamente.