Función decreciente

Una función y=f(x) se denomina decreciente en un intervalo I=(a,b) si, para cualesquiera dos puntos x₁, x₂ del intervalo con x₁<x₂, se verifica que $$ f(x_1) \ge f(x_2) $$. En cambio, se dice que es estrictamente decreciente cuando se cumple $$ f(x_1) > f(x_2) $$.

Una función estrictamente decreciente suele describirse también como “decreciente en sentido estricto”.

Las funciones decrecientes y las estrictamente decrecientes constituyen casos particulares de la clase más general de las funciones monótonas.

Observación. Una función es monótona en un intervalo de su dominio cuando, en todo ese intervalo, se mantiene siempre no decreciente o siempre no creciente.

Ejemplo

Consideremos la función

$$ y=x^2 $$

Esta función es estrictamente decreciente en el intervalo (-4,0), ya que para cualesquiera dos valores x₁<x₂ dentro de dicho intervalo se cumple f(x₁)>f(x₂).

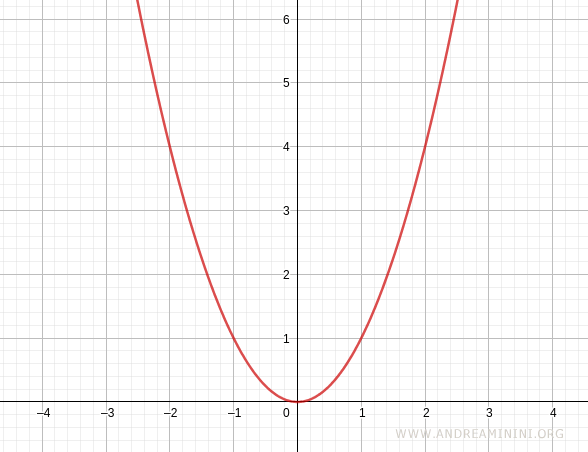
En cambio, la misma función deja de ser decreciente en el intervalo (0,4).

Observación. La monotonía de una función continua y derivable puede determinarse también analizando el signo de su derivada primera, f'(x).

Y así sucesivamente.