Función Uniformemente Continua

Se dice que una función es uniformemente continua en el intervalo [a, b] ⊆ ℝ si, para todo $ \epsilon > 0 $, existe un $ \delta = \delta(\epsilon) > 0 $ tal que $$ |x - x'| < \delta \quad \Rightarrow \quad |f(x) - f(x')| < \epsilon $$ para cualesquiera $ x, x' \in [a, b] $.

En términos geométricos, esto significa que una función continua en [a, b] nunca presenta oscilaciones bruscas ni descontroladas.

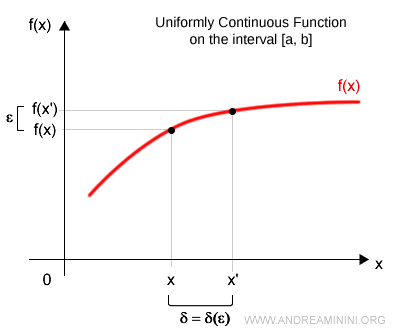
uniformly continuous function

De forma intuitiva, cuanto más pequeño es $ \epsilon $, más reducido debe ser también el valor de $ \delta $, y viceversa.

En general, para una función continua cualquiera, $ \delta $ puede depender tanto de $ \epsilon $ como del punto concreto $ x_0 $ en el que se estudia la continuidad:

$$ \delta = \delta(\epsilon, x_0) $$

En cambio, en el caso de las funciones uniformemente continuas, la elección de $ \delta $ depende únicamente de $ \epsilon $, con independencia del punto $ x_0 $.

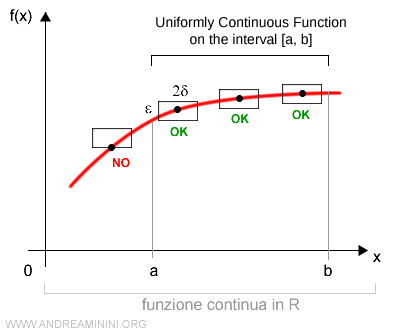
Nota: La relación entre $ \epsilon $ y $ \delta $ puede visualizarse como un rectángulo centrado en cualquier punto $ x \in [a, b] $. Para una función uniformemente continua, la gráfica solo llega a tocar los lados verticales de dicho rectángulo, sin llegar nunca a cortar el borde horizontal. Por ejemplo, si se puede escoger $ \delta = 2\epsilon $ en el intervalo [a, b], la gráfica intersecta estos rectángulos únicamente en los lados verticales, lo cual confirma la continuidad uniforme. En cambio, si en un intervalo como [0, a] la función únicamente cumple $ \delta = \epsilon/2 $ y su gráfica atraviesa el lado inferior del rectángulo, la continuidad uniforme deja de cumplirse en ese intervalo.
example

Un Ejemplo Práctico
Diferencia entre Continuidad y Continuidad Uniforme

Un Ejemplo Práctico

Consideremos la función $ f(x) = x^3 $, que es continua en ℝ:

$$ f(x) = x^3 $$

Esta función resulta ser uniformemente continua en el intervalo [0, 1].

Sea $ \epsilon > 0 $. La continuidad uniforme garantiza la existencia de un $ \delta > 0 $ (dependiendo únicamente de $ \epsilon $) tal que para todo $ x_1, x_2 \in [0, 1] $:

$$ |x_1 - x_2| < \delta \quad \Rightarrow \quad |x_1^3 - x_2^3| < \epsilon $$

Recordemos que la diferencia de cubos se descompone como:

$$ |x_1^3 - x_2^3| = |x_1 - x_2| \cdot |x_1^2 + x_1x_2 + x_2^2|, $$

y dado que para $ x_1,x_2 \in [0,1] $ se cumple

$$ 0 \le x_1^2,\, x_1x_2,\, x_2^2 \le 1, $$

tenemos entonces que

$$ |x_1^2 + x_1x_2 + x_2^2| \le 3, $$

lo cual implica

$$ |x_1^3 - x_2^3| \le 3\, |x_1 - x_2|. $$

Por tanto, para garantizar que $ |x_1^3 - x_2^3| < \epsilon $, basta imponer

$$ 3\,|x_1 - x_2| < \epsilon, $$ lo que equivale a

$$ |x_1 - x_2| < \frac{\epsilon}{3}. $$

En conclusión, para todo $ \epsilon > 0 $ se puede elegir

$$ \delta = \frac{\epsilon}{3}, $$

con lo cual queda demostrado que $ f(x) = x^3 $ es uniformemente continua en [0, 1].

Diferencia entre Continuidad y Continuidad Uniforme

Aunque ambos conceptos están relacionados, no son equivalentes:

Una función uniformemente continua en [a, b] es necesariamente continua, con un $ \delta $ escogido de manera uniforme en todo el intervalo, es decir, $ \delta = \delta(\epsilon) $, independiente del punto considerado.
Una función continua en [a, b] puede requerir un $ \delta $ que dependa tanto de $ \epsilon $ como del punto $ x_0 $, es decir, $ \delta = \delta(\epsilon, x_0) $, sin asegurar un comportamiento uniforme en el intervalo.

De este modo, la continuidad uniforme constituye una condición estrictamente más fuerte que la mera continuidad.

Nota: En resumen, aunque la continuidad es condición necesaria para la continuidad uniforme, por sí sola no basta.

Y así sucesivamente.