Preimágenes de una función

La preimagen (o imagen inversa) de un elemento \( y \in Y \) en el codominio de una función \( f: X \to Y \) es el conjunto de todos los elementos \( x \in X \) del dominio que se asignan a \( y \); en otras palabras, todos aquellos \( x \) tales que \( f(x) = y \). La preimagen de \( y \) se denota: $$ f^{-1}(\{y\}) = \{ x \in X \mid f(x) = y \} $$

Dicho de forma sencilla, la preimagen de un elemento \( y \) en el codominio \( Y \) está constituida por todos los valores del dominio \( X \) que, al aplicarse en la función \( f(x) \), producen \( y \) como resultado.

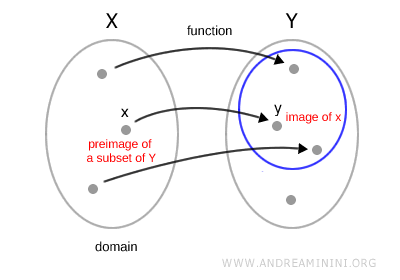
De manera más general, la preimagen de un subconjunto de \( Y \) mediante una función \( y = f(x) \) es el conjunto de todos los elementos del dominio \( X \) que la función envía a ese subconjunto del codominio.

La preimagen de un conjunto nos indica qué elementos del dominio se corresponden con un subconjunto dado a través de la función \( f \).

Conviene subrayar que la preimagen \( f^{-1}(y) \) de un elemento \( y \) no coincide necesariamente con la función inversa, ya que puede asociar un mismo elemento del codominio con varios elementos del dominio (es decir, define una relación y no una función propiamente dicha).

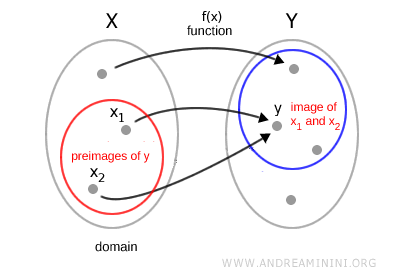
Esto ocurre porque una función no está obligada a ser inyectiva: un único elemento del codominio puede corresponderse con distintos elementos del dominio.

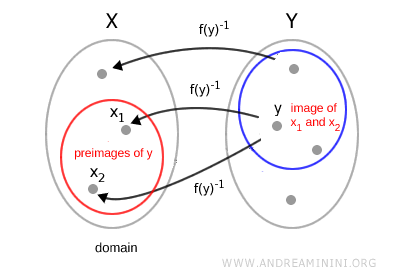
La preimagen está siempre bien definida, con independencia de que la función sea inyectiva o suprayectiva.

Además, la preimagen de un subconjunto puede ser vacía si ningún elemento del dominio se mapea en él.

Diferencia entre función y relación. Una función asigna a cada elemento del dominio exactamente un elemento del codominio. Una relación, en cambio, puede asociar un mismo elemento del codominio con uno o varios elementos del dominio. Por tanto, toda función es una relación, pero no toda relación es una función.

Un ejemplo práctico

Consideremos la función \( f(x) = x^2 \).

El dominio es el conjunto de los números reales \( \mathbb{R} \), y el codominio el conjunto de los números reales no negativos \( \mathbb{R}^{\geq 0} \).

Si tomamos un elemento del codominio, por ejemplo \( 4 \), la preimagen de \( 4 \) es el conjunto de todos los \( x \) en el dominio tales que \( x^2 = 4 \):

$$ f^{-1}(\{4\}) = \{ -2, 2 \} $$

En este caso, \( -2 \) y \( 2 \), ya que tanto \( (-2)^2 = 4 \) como \( 2^2 = 4 \).

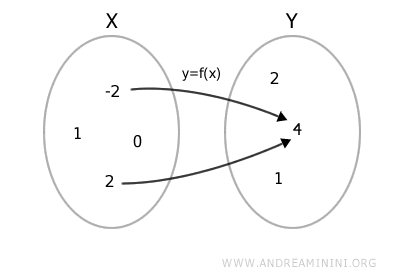
Así, la preimagen de \( 4 \) es el conjunto \( \{ -2, 2 \} \), pues son exactamente los elementos del dominio que se mapean en \( 4 \) bajo \( x^2 \). 

Nota. En este ejemplo, las preimágenes en \( Y \) no definen una función inversa, sino una relación inversa.

Propiedades de las preimágenes

Las propiedades fundamentales de las preimágenes bajo una función son las siguientes:

• Preimagen de una unión
  La preimagen de la unión de dos conjuntos es igual a la unión de sus preimágenes: $$ f^{-1}(A \cup B) = f^{-1}(A) \cup f^{-1}(B) $$
• Preimagen de una intersección
  La preimagen de la intersección de dos conjuntos es igual a la intersección de sus preimágenes: $$ f^{-1}(A \cap B) = f^{-1}(A) \cap f^{-1}(B) $$
• Preimagen de un complemento
  La preimagen del complemento de un conjunto es igual al complemento de su preimagen: $$ f^{-1}(Y \setminus A) = X \setminus f^{-1}(A) $$

A estas propiedades se las conoce como propiedades de preservación de la preimagen respecto a la unión, la intersección y el complemento.

Ejemplo

Consideremos ahora la función:

$$ f(x) = \sqrt{x} $$

donde \( f: \mathbb{R}^{\geq 0} \to \mathbb{R}^{\geq 0} \), ya que la raíz cuadrada solo está definida para \( x \geq 0 \).

Tomemos dos subconjuntos del dominio:

$$ A_1 = [0, 1) $$

$$ A_2 = [4, 9] $$

La preimagen del intervalo \( A_1 = [0, 1) \) es:

$$ f^{-1}(A_1) = \{ x \in \mathbb{R}^{\geq 0} \mid \sqrt{x} \in [0, 1) \} = [0, 1) $$

La preimagen de \( A_2 = [4, 9] \) resulta ser:

$$ f^{-1}(A_2) = \{ x \in \mathbb{R}^{\geq 0} \mid \sqrt{x} \in [4, 9] \} = [16, 81] $$

Analicemos ahora las tres operaciones de conjuntos:

A] Unión

La unión de las preimágenes es:

$$ f^{-1}(A_1) \cup f^{-1}(A_2) = [0, 1) \cup [16, 81] $$

La unión de los intervalos es:

$$ A_1 \cup A_2 = [0, 1) \cup [4, 9] $$

Por lo tanto, la preimagen de la unión es:

$$ f^{-1}(A_1 \cup A_2) = f^{-1}([0, 1) \cup [4, 9]) = [0, 1) \cup [16, 81] $$

Esto confirma que \( f(x) = \sqrt{x} \) preserva las uniones:

$$ f^{-1}(A_1 \cup A_2) = f^{-1}(A_1) \cup f^{-1}(A_2) $$

B] Intersección

La intersección de las preimágenes es el conjunto vacío, ya que no hay intersección entre \( [0, 1) \) y \( [4, 9] \):

$$ f^{-1}(A_1) \cap f^{-1}(A_2) = [0, 1) \cap [16, 81] = \emptyset $$

Del mismo modo, la preimagen de la intersección también es vacía:

$$ f^{-1}(A_1 \cap A_2) = f^{-1}(\emptyset) = \emptyset $$

Así se confirma que \( f(x) = \sqrt{x} \) preserva las intersecciones:

$$ f^{-1}(A_1 \cap A_2) = f^{-1}(A_1) \cap f^{-1}(A_2) $$

C] Complemento

Consideremos ahora el complemento de \( A_1 = [0, 1) \) en \( \mathbb{R}^{+} \):

$$ \mathbb{R}^{+} \setminus A_1 = [1, \infty) $$

La preimagen del complemento es:

$$ f^{-1}(\mathbb{R}^{+} \setminus A_1) = f^{-1}([1, \infty)) = [1, \infty) $$

El complemento de la preimagen de \( A_1 \) es:

$$ \mathbb{R}^{+} \setminus f^{-1}(A_1) = \mathbb{R}^{+} \setminus [0, 1) = [1, \infty) $$

En consecuencia, \( f(x) = \sqrt{x} \) también preserva los complementos:

$$ f^{-1}(\mathbb{R}^{+} \setminus A_1) = \mathbb{R}^{+} \setminus f^{-1}(A_1) $$

En este ejemplo se cumplen todas las propiedades esenciales de las preimágenes en relación con la unión, la intersección y el complemento.

Y así sucesivamente.