Función Característica

En teoría de conjuntos, la función característica (también llamada función indicadora) de un subconjunto A de un conjunto X se define como: $$ \chi_A : X \rightarrow \{ 0, 1 \} $$ donde $$ \begin{cases} \chi_A(x) = 1 \:\: \text{si} \:\: x \in A \\ \chi_A(x) = 0 \:\: \text{si} \:\: x \notin A \end{cases} $$

Ejemplo práctico

Sea el conjunto X:

$$ X = \{ 1, 2, 3, 4, 5, 6, 7 \} $$

y consideremos el subconjunto A:

$$ A = \{ 4, 5, 6 \} $$

La función característica $$ \chi_A $$ se expresa entonces como:

$$ \chi_A(1) = 0 \\ \chi_A(2) = 0 \\ \chi_A(3) = 0 \\ \chi_A(4) = 1 \\ \chi_A(5) = 1 \\ \chi_A(6) = 1 \\ \chi_A(7) = 0 $$

Esta es la función característica asociada al subconjunto A.

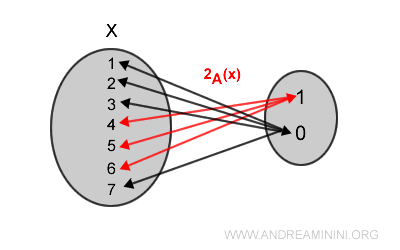
De este modo, la preimagen de 1 mediante $$ \chi_A $$ coincide con los elementos de A:

$$ \chi_A^{-1}(1) = \{ 4, 5, 6 \} $$

En otras palabras, para cualquier conjunto X, si tomamos $$ 2 = \{ 0, 1 \} $$, existe una correspondencia biyectiva entre el conjunto potencia $$ \mathcal{P}(X) $$ y el conjunto $$ 2^X $$ de todas las funciones de X en {0, 1}.

Y así sucesivamente.