Tipos de Funciones

Existen diferentes tipos de funciones. A continuación se presentan las categorías principales:

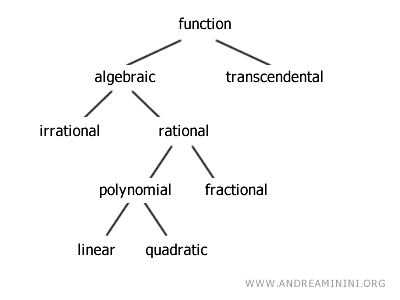
• Funciones Algebraicas
  Una función se considera algebraica cuando su expresión f(x) involucra únicamente operaciones de suma, resta, multiplicación, potencias o raíces.

  Ejemplo. Son funciones algebraicas: $$ y=2x^2+x $$ $$ y= \frac{x+1}{x-1} $$ $$ y = x - \sqrt{x} $$

• Funciones Trascendentes
  Una función es trascendente cuando no es algebraica.

  Ejemplo. Pertenecen a esta categoría las funciones que incluyen expresiones exponenciales como \( a^x \), logaritmos o funciones trigonométricas: $$ y=2^x $$ $$ y= \sin(x) $$ $$ y = \log(x) $$

Las funciones algebraicas, a su vez, pueden subdividirse en racionales e irracionales:

• Funciones Racionales
  Una función es racional cuando la variable independiente x no aparece bajo un radical.

  Ejemplo. Son funciones racionales: $$ y = x^2+1 $$ $$ y = \frac{2x+1}{x-1} $$ $$ y = x^3-x^2+2 $$

• Funciones Irracionales
  Una función es irracional cuando la variable independiente x aparece al menos una vez bajo un signo radical.

  Ejemplo. Son funciones irracionales: $$ y = \sqrt{x} $$ $$ y = x - \sqrt{x} $$ $$ y = \frac{ \sqrt{x} }{x+1} $$

Las funciones racionales, por su parte, se clasifican en polinómicas (también llamadas enteras) y fraccionarias:

• Funciones Polinómicas (Enteras)
  Una función se considera polinómica cuando su expresión f(x) es un polinomio de cualquier grado.
  • Funciones Lineales
    cuando el polinomio es de primer grado
  • Funciones Cuadráticas
    cuando el polinomio es de segundo grado

  Ejemplo. Ejemplos de funciones polinómicas lineales: $$ y = 2x+1 $$ $$ y = 5-3x $$ Ejemplos de funciones polinómicas cuadráticas: $$ y = x^2-3x+1 $$ $$ y = 3x^2+2x+1 $$ Otros ejemplos de funciones polinómicas que no son ni lineales ni cuadráticas: $$ y = 2x^3+x^2-1 $$ $$ y = x^5-3x^3+2 $$

• Funciones Racionales Fraccionarias
  Una función es racional fraccionaria cuando f(x) se expresa como el cociente de dos polinomios.

  Ejemplo. Son funciones racionales fraccionarias: $$ y = \frac{x+1}{x-1} $$ $$ y = \frac{x^2+2x-1}{x^3+x^2+4} $$ $$ y = \frac{x^4+x-1}{x^2+3} $$

Y así sucesivamente.