Teorema de Heine - Cantor

Si una función \( f(x) \) es continua en un intervalo cerrado y acotado [a, b], entonces es uniformemente continua en [a, b].

El teorema de Heine - Cantor enuncia una condición suficiente para la continuidad uniforme.

En términos generales, la continuidad de una función no implica necesariamente su continuidad uniforme.

Sin embargo, la continuidad en un intervalo cerrado y acotado resulta suficiente para garantizar también la continuidad uniforme.

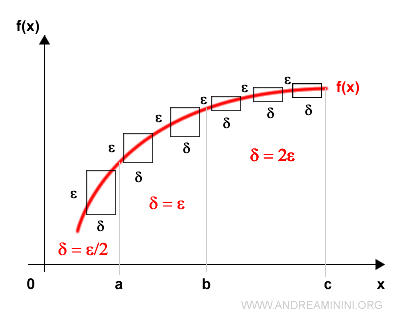
Explicación: En un intervalo cerrado [a, b] buscamos una relación \( \delta = \delta(\epsilon) \) que asegure la continuidad uniforme. Dicha relación solo tiene validez dentro de [a, b]; en otros intervalos puede ser necesaria una función distinta \( \delta = \delta'(\epsilon) \). La única hipótesis requerida es que la función sea continua en el intervalo de estudio. Así, en el diagrama anterior, la función resulta uniformemente continua en [b, c] con \( \delta = 2\epsilon \), y en [a, b] con \( \delta = \epsilon \). En cambio, en [0, a] la función es meramente continua, satisfaciendo \( \delta = \epsilon / 2 \). En este último caso, la continuidad uniforme falla en la vecindad derecha de 0, donde la gráfica se eleva bruscamente. Conforme al teorema de Heine - Cantor, para restablecer la continuidad uniforme es preciso restringirse a un subintervalo menor, como [0.5, a], donde la función vuelve a ser uniformemente continua con \( \delta = \epsilon / 3 \).

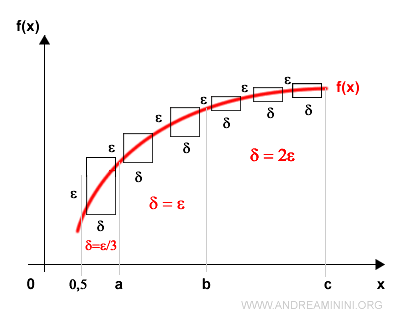
Por el contrario, en [0, 0.5] la función permanece continua, pero deja de ser uniformemente continua. Y así sucesivamente.

Demostración

La demostración se lleva a cabo mediante un argumento por contradicción.

Supongamos que existe un \( \epsilon_0 > 0 \) tal que, para todo \( \delta > 0 \), pueden hallarse puntos \( x, x' \in [a, b] \) que cumplen:

$$ \exists \epsilon_0 > 0 : \forall \delta > 0,\ \exists x,x' \in [a, b] \text{ tales que } |x - x'| < \delta \text{ y } |f(x) - f(x')| \ge \epsilon_0 $$

Esta proposición constituye exactamente la negación lógica de la definición de continuidad uniforme.

Nota: Por definición, una función es uniformemente continua en [a, b] si: $$ \forall \epsilon > 0,\ \exists \delta > 0\ \text{ tal que } \forall x,x' \in [a, b],\ |x - x'| < \delta \Rightarrow |f(x) - f(x')| \le \epsilon $$

Consideremos ahora \( \delta = 1/n \), con \( n \in \mathbb{N} \). Entonces la hipótesis inicial se reformula así:

$$ \exists \epsilon_0 > 0 : \forall n \in \mathbb{N},\ \exists x_n, x_n' \in [a, b]\ \text{ tales que } |x_n - x_n'| < \frac{1}{n},\ |f(x_n) - f(x_n')| \ge \epsilon_0 $$

Por el teorema de Bolzano - Weierstrass, la sucesión \( x_n \) admite una subsucesión convergente \( x_{n_k} \). Como \( x_n' \) dista menos de \( 1/n \) de \( x_n \), se cumple que:

$$ x_{n_k} - \frac{1}{n_k} < x_{n_k}' < x_{n_k} + \frac{1}{n_k} $$

De este modo, tanto \( x_{n_k} \) como \( x_{n_k}' \) convergen al mismo límite \( x_0 \in [a, b] \).

Por el teorema del sándwich, se sigue que:

$$ \lim_{k \to \infty} x_{n_k}' = x_0 $$

Y dado que \( f \) es continua en [a, b], el límite de la diferencia se anula necesariamente:

$$ \lim_{k \to \infty} [f(x_{n_k}) - f(x_{n_k}')] = f(x_0) - f(x_0) = 0 $$

Lo cual contradice la hipótesis inicial, que afirmaba:

$$ |f(x_n) - f(x_n')| \ge \epsilon_0 $$

Por tanto, la suposición resulta falsa y el teorema queda demostrado por contradicción.

Y así sucesivamente.