Funciones compuestas

¿Qué es una función compuesta?

Se denomina función compuesta a aquella en la que el dominio de una función coincide con el codominio (o recorrido) de otra. $$ h(x) = f(g(x)) $$ Esto se lee como f de g de x.

La función compuesta también suele representarse como:

$$ h = f \circ g $$

y se lee como f compuesta con g.

En este contexto, el codominio de g pasa a ser el dominio de f.

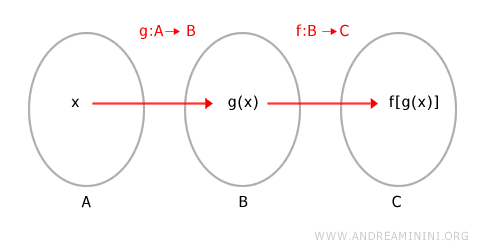
Observación. El conjunto A representa el dominio de g. El conjunto B corresponde al recorrido de g - que a la vez constituye el codominio de g y el dominio de f - . El conjunto C contiene los valores de salida de f, que son también los de la función compuesta f[g(x)].

Un ejemplo práctico

Consideremos las siguientes dos funciones:

$$ f(x) = \frac{1}{x} $$

$$ g(x) = \sin x $$

La función compuesta h(x), definida como f(g(x)), es:

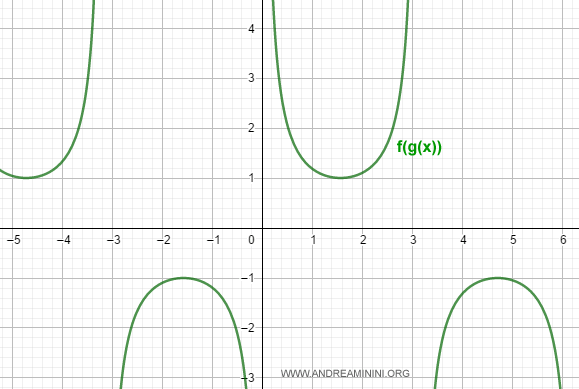
$$ h(x) = f(g(x)) = \frac{1}{g(x)} = \frac{1}{\sin x} $$

En este caso, el dominio de f debe corresponder al recorrido de g, que es el intervalo [0,1].

La gráfica de la función compuesta f(g(x)) se muestra a continuación:

Propiedades de las funciones compuestas

Las propiedades más relevantes de las funciones compuestas son:

• No son conmutativas. En general: $$ g[f(x)] \ne f[g(x)] $$

  Ejemplo. Consideremos dos funciones: $$ f(x) = x+1 $$ $$ g(x) = 2x+3 $$ La función compuesta g[f(x)] resulta: $$ g(f(x)) = g(x+1) = 2(x+1) + 3 = 2x + 5 $$ En cambio, la función compuesta f[g(x)] es: $$ f(g(x)) = f(2x+3) = (2x+3) + 1 = 2x + 4 $$ Se trata claramente de dos funciones distintas.

• Sí cumplen la propiedad asociativa: $$ h \circ (g \circ f) = (h \circ g) \circ f $$

  Ejemplo. Consideremos tres funciones: $$ f(x) = x+1 $$ $$ g(x) = 2x+3 $$ $$ h(x) = -x $$ La función compuesta h o (g o f) es: $$ h \circ (g \circ f) = h \circ [2(x+1) + 3] = h \circ [2x + 5] = -[2x + 5] = -2x - 5 $$ Por su parte, la función compuesta (h o g) o f resulta: $$ (h \circ g) \circ f = -(2x + 3) \circ f = -2x - 3 \circ f = -2(x + 1) - 3 = -2x - 5 $$ En ambos casos se obtiene el mismo resultado.

• Si el recorrido de f[g(x)] coincide con el dominio de g(x) - es decir, si A = C -
  

  

  
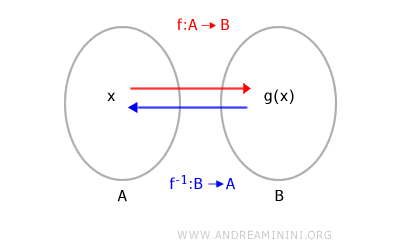
  entonces es posible definir también la función compuesta g[f(x)]. No obstante, en general: $$ f[g(x)] \ne g[f(x)] $$ ya que la composición de funciones no cumple la propiedad conmutativa.
• La composición de una función f:A→B con su función inversa f^-1:B→A devuelve cada elemento de entrada x a sí mismo: $$ f^{-1}[f(x)] = x $$ Esta composición particular recibe el nombre de función identidad.
  

Y así sucesivamente.