Traslación de funciones

Una traslación de funciones es una transformación geométrica que desplaza la gráfica de una función sin modificar su forma.

En términos más precisos, se trata de un desplazamiento rígido de la gráfica en el plano cartesiano.

Cuando decimos que el desplazamiento es "rígido", queremos indicar que no hay deformaciones: la gráfica conserva exactamente su forma y su curvatura.

Una traslación puede realizarse de varias maneras: a lo largo del eje x, a lo largo del eje y, o de forma simultánea en ambos ejes.

¿Para qué se utiliza? Las traslaciones son especialmente útiles para estudiar cómo cambia una función cuando se modifican sus parámetros. Además, suelen ser el punto de partida para analizar transformaciones más avanzadas, como las dilataciones y las reflexiones. En aplicaciones reales, por ejemplo en telecomunicaciones, las traslaciones horizontales se emplean para representar el retardo temporal de una señal.

Traslación horizontal
Traslación vertical
Traslación combinada

Traslación horizontal

Partiendo de una función genérica $ y = f(x) $, una traslación horizontal de $ a $ unidades se obtiene modificando el argumento de la función:

$ y = f(x - a) $ desplaza la gráfica $ a $ unidades hacia la derecha.
$ y = f(x + a) $ desplaza la gráfica $ a $ unidades hacia la izquierda.

Es importante tener en cuenta que este tipo de desplazamiento puede resultar contraintuitivo. Aunque parezca extraño, restar $ a $ dentro del argumento provoca un desplazamiento hacia la derecha, mientras que sumar $ a $ desplaza la gráfica hacia la izquierda.

Ejemplo práctico

Consideremos la función $ f(x) = x^2 $.

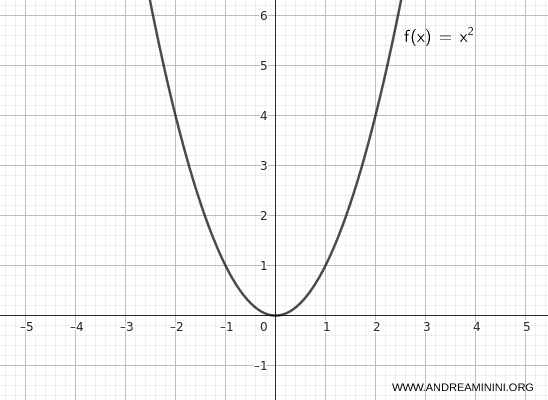
gráfica de la función y igual a x al cuadrado

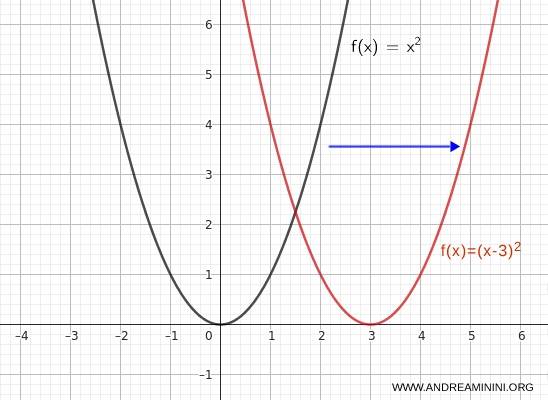
Si trasladamos la gráfica hacia la derecha, obtenemos:

$$ y = (x - 3)^2 $$

En este caso, el vértice de la parábola pasa de $ (0, 0) $ a $ (3, 0) $.

traslación horizontal de una parábola hacia la derecha

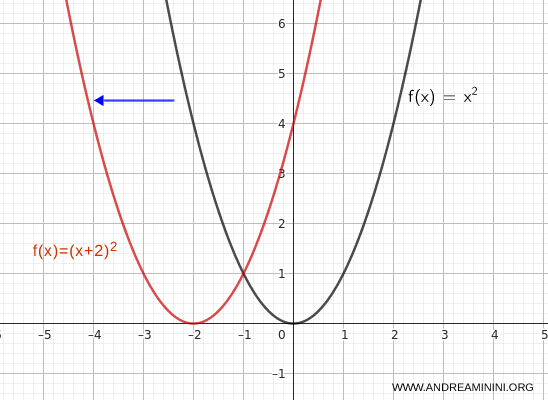
Si ahora trasladamos la gráfica hacia la izquierda, escribimos:

$$ y = (x + 2)^2 $$

El vértice se desplaza entonces de $ (0, 0) $ a $ (-2, 0) $.

traslación horizontal de una parábola hacia la izquierda

Traslación vertical

Partiendo de una función $ y = f(x) $, una traslación vertical de $ b $ unidades se obtiene sumando o restando una constante a la función.

$ y = f(x) + b $ desplaza la gráfica $ b $ unidades hacia arriba.
$ y = f(x) - b $ desplaza la gráfica $ b $ unidades hacia abajo.

En este caso, el efecto del signo es directo e intuitivo: el signo positivo desplaza la gráfica hacia arriba y el signo negativo la desplaza hacia abajo.

Ejemplo práctico

Volvemos a considerar la función

$$ f(x) = x^2 $$

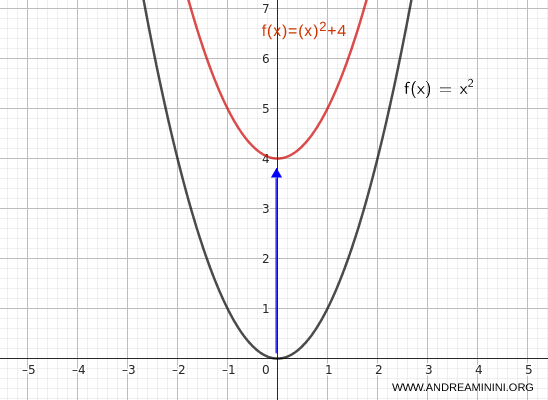
Para trasladar la gráfica 4 unidades hacia arriba, escribimos:

$$ y = x^2 + 4 $$

El vértice de la parábola se desplaza de $ (0, 0) $ a $ (0, 4) $.

traslación vertical de una parábola hacia arriba

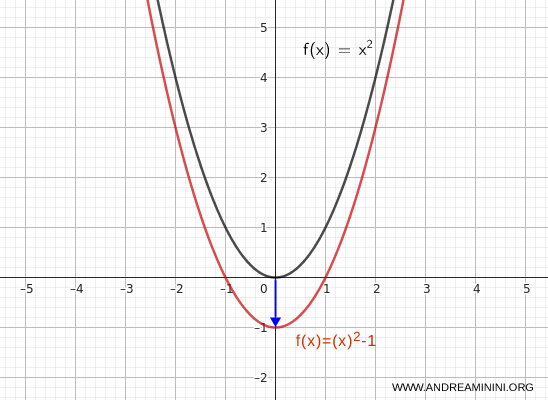
Si, en cambio, trasladamos la gráfica 1 unidad hacia abajo, obtenemos:

$$ y = x^2 - 1 $$

En este caso, el vértice se sitúa en $ (0, -1) $.

traslación vertical de una parábola hacia abajo

Traslación combinada

Una traslación combinada consiste en aplicar simultáneamente una traslación horizontal y una traslación vertical.

$ y = f(x - a) + b $ desplaza la gráfica $ a $ unidades hacia la derecha y $ b $ unidades hacia arriba.
$ y = f(x + a) - b $ desplaza la gráfica $ a $ unidades hacia la izquierda y $ b $ unidades hacia abajo.

Ejemplo

Consideremos de nuevo la función

$$ f(x) = x^2 $$

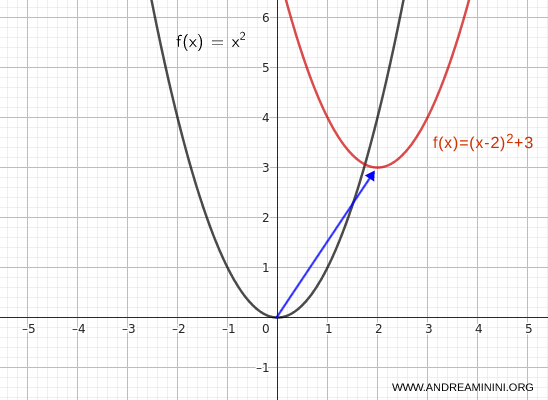
Para trasladar la gráfica 2 unidades hacia la derecha y 3 unidades hacia arriba, escribimos:

$$ y = (x - 2)^2 + 3 $$

Como resultado de ambas traslaciones, el vértice de la parábola pasa de $ (0, 0) $ a $ (2, 3) $.

traslación combinada horizontal y vertical de una parábola

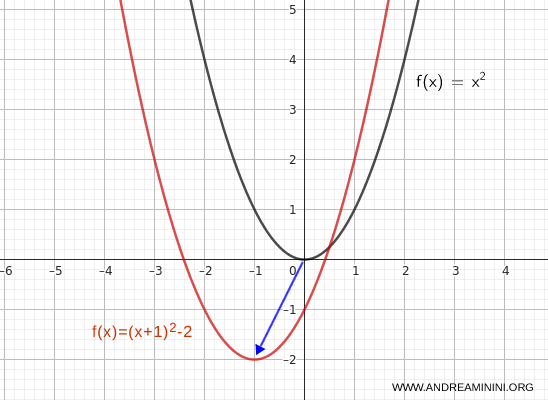
De manera análoga, si trasladamos la gráfica 1 unidad hacia la izquierda y 2 unidades hacia abajo, escribimos:

$$ y = (x + 1)^2 - 2 $$

En este caso, el vértice se desplaza al punto $ (-1, -2) $.

ejemplo de traslación combinada de una parábola

Y así sucesivamente.