Máximos y mínimos de una función
Los máximos y mínimos de una función son los puntos de un intervalo $ x \in [a, b] $ en los que la función $ y = f(x) $ alcanza, respectivamente, su valor más alto y su valor más bajo.
Estos extremos pueden clasificarse en absolutos o relativos:
- Máximo o mínimo absoluto: Punto en el que $ f(x) $ alcanza su valor mayor o menor en todo el intervalo $ [a, b] $.
- Máximo o mínimo relativo (local): Punto en el que $ f(x) $ alcanza un valor mayor o menor únicamente respecto a los puntos de un entorno de $ x_0 $.
Ejemplo
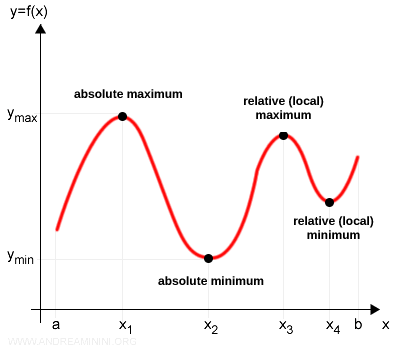
En $ x_1 $, la función $ f(x) $ alcanza un máximo absoluto en $ [a, b] $, y en $ x_2 $ alcanza un mínimo absoluto.
En cambio, en $ x_3 $ y $ x_4 $, la función presenta únicamente un máximo y un mínimo relativos, respectivamente.
Nota: Un máximo (o mínimo) absoluto en $ [a, b] $ es, por definición, también un máximo (o mínimo) relativo en cualquier entorno de ese punto. Así, $ x_1 $ es simultáneamente un máximo absoluto y relativo, mientras que $ x_2 $ es a la vez un mínimo absoluto y relativo.
Máximos y mínimos relativos
Sea $$ x_0 $$ un punto del dominio y consideremos todos los puntos de un entorno de radio $ \delta $ alrededor de $ x_0 $:
$$ |x - x_0| < \delta $$
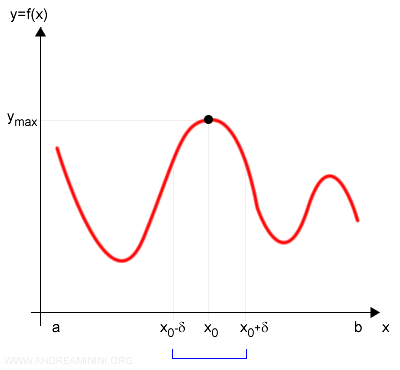
Si $ f(x_0) $ es mayor que los valores de $ f(x) $ en dicho entorno, entonces $ x_0 $ es un máximo relativo:
$$ f(x_0) > f(x) $$
Por ejemplo:
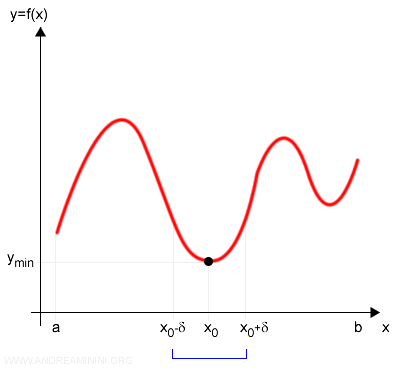
De manera análoga, si $ f(x_0) $ es menor que todos los valores de $ f(x) $ en ese entorno, entonces $ x_0 $ es un mínimo relativo:
$$ f(x_0) < f(x) $$
Por ejemplo:
Nota: En el caso de los extremos relativos, la desigualdad (mayor o menor) solo se cumple dentro de un entorno de $ x_0 $, y no necesariamente en todo el intervalo $ [a, b] $ donde está definida la función.
Y así sucesivamente.