Funciones Pares

¿Qué es una función par?

Una función se denomina par si, para todo x en su dominio, se cumple la siguiente condición: $$ f(x) = f(-x) \quad \forall \ x \in D $$

Cuando una función es par, su gráfica presenta simetría respecto al eje y, ya que para cada punto P(x, y), existe un punto correspondiente P(-x, y).

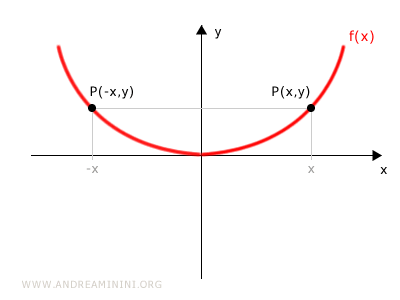
¿Cómo comprobar si una función es par?

• Desde el enfoque analítico, se calcula f(-x) sustituyendo x por su opuesto -x y se compara el resultado con f(x). Si ambos coinciden, la función es par. $$ f(-x) = f(x) $$

  Ejemplo: Consideremos la función f(x) = x². Sustituyamos x por -x y comprobemos si obtenemos el mismo resultado. $$ f(-x) = (-x)^2 = x^2 = f(x) $$ Como f(-x) coincide con f(x), la función es par.

• Desde el punto de vista gráfico, basta observar si la gráfica es simétrica con respecto al eje y.
  

  

Nota: Que una función no sea par no significa necesariamente que sea impar, y viceversa. Por ejemplo, la función f(x) = x² + x no es ni par ni impar.

Un ejemplo práctico

Un ejemplo clásico de función par es la función coseno.

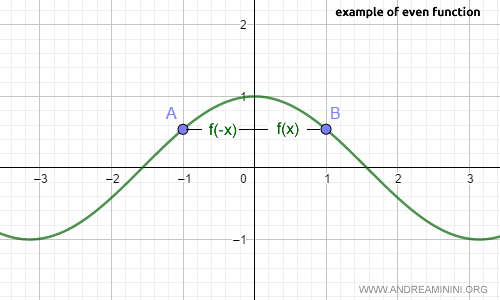
Para cualquier valor de x en el dominio de la función coseno, se cumple que f(x) = f(-x), y su gráfica es simétrica respecto al eje y.

Nota: Por ejemplo, para x = 1 y x = -1, la función coseno devuelve el mismo valor, es decir, f(1) = f(-1), y así sucesivamente.

Ejemplo 2

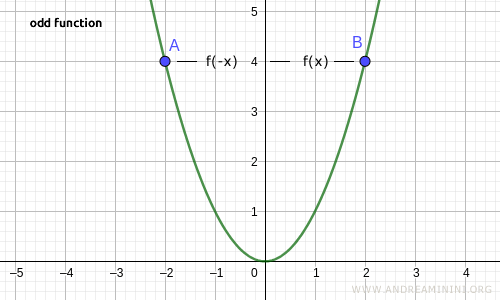
Otra función par es f(x) = x².

$$ f(x) = x^2 $$ $$ f(-x) = (-x)^2 = x^2 $$

También en este caso, para cualquier valor de x en el dominio, se cumple que f(x) = f(-x).

Nota: En general, si una función está compuesta únicamente por potencias de x con exponentes pares, es una función par.

Ejemplo 3

Analicemos si la siguiente función es par:

$$ f(x) = x^2 + x $$

Sustituyamos x por -x en la expresión de la función:

$$ f(-x) = (-x)^2 + (-x) = x^2 - x $$

El resultado es diferente de f(x) = x² + x.

Por tanto, esta función no es par.

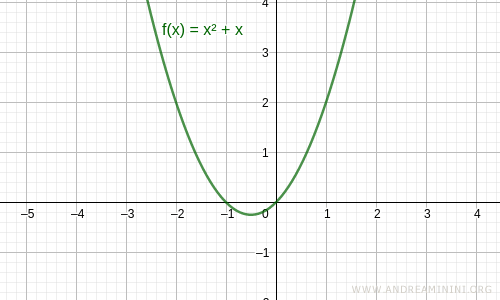
Nota: La función f(x) = x² + x tampoco es impar.

Y así sucesivamente.