Dilatación y contracción horizontal y vertical de una función
Una dilatación es una transformación geométrica que modifica el gráfico de una función en el plano cartesiano reescalando las distancias a lo largo de uno de los ejes, conservando la simetría del gráfico y manteniendo fijo el origen.
La transformación actúa sobre uno de los dos ejes de coordenadas: el eje horizontal (x) o el eje vertical (y).
Según el valor del factor de transformación, el gráfico se dilata o se contrae.
Dilatación horizontal
La dilatación horizontal se produce cuando la variable independiente $x$ se modifica dentro de la función.
$$ y = f\left( \dfrac{x}{m} \right) \quad \text{con } m > 1 $$
El gráfico se dilata horizontalmente con respecto al origen $O$. Cada punto del gráfico se desplaza a una posición más alejada del origen a lo largo del eje $x$.
Ejemplo
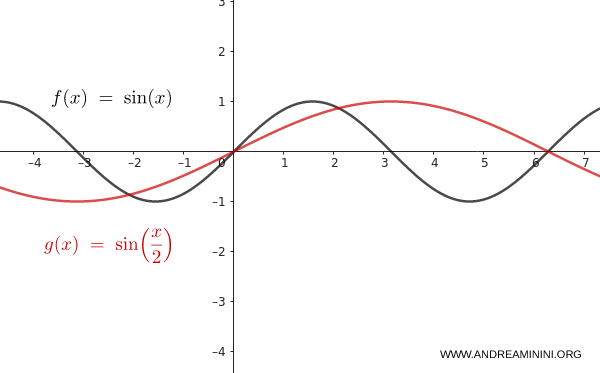
Consideremos la función $f(x) = \sin(x)$.
Aplicamos una dilatación horizontal con $m = 2$:
$$ y = \sin\left( \dfrac{x}{2} \right) $$
El período se duplica. La onda seno necesita ahora el doble de distancia horizontal para completar un ciclo completo. Esto corresponde a una dilatación horizontal.
Contracción horizontal
La contracción horizontal se da cuando el factor cumple $0 < m < 1$.
$$ y = f\left( \dfrac{x}{m} \right) \quad \text{con } 0 < m < 1 $$
Todos los puntos del gráfico se acercan al eje $y$, lo que produce una contracción en la dirección horizontal.
Ejemplo
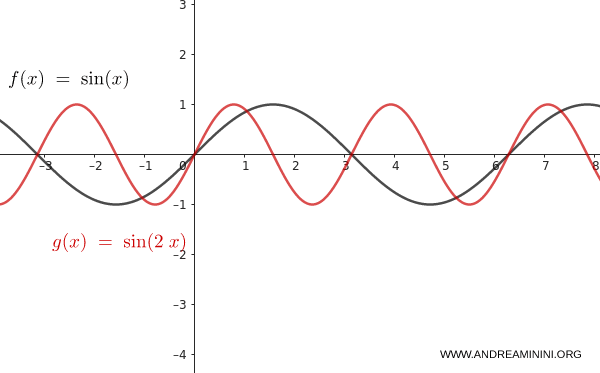
De nuevo, consideremos la función $f(x) = \sin(x)$.
Aplicamos una contracción horizontal con $m = \frac{1}{2}$:
$$ y = \sin(2x) $$
El período se reduce a la mitad. La función completa dos ciclos completos en el mismo intervalo en el que la función original completaba uno. Esto es una contracción horizontal.
Dilatación vertical
La dilatación vertical afecta a toda la función multiplicándola por una constante $n$:
$$ y = n \cdot f(x) \quad \text{con } n > 1 $$
El gráfico se extiende hacia arriba y hacia abajo con respecto al eje $x$. Todos los valores de $y$ aumentan en valor absoluto.
Ejemplo
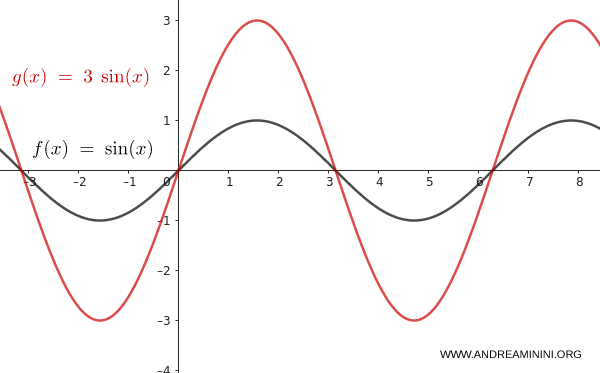
Tomemos la función $f(x) = \sin(x)$.
Aplicamos una dilatación vertical con $n = 3$:
$$ y = 3 \cdot \sin(x) $$
La amplitud de la onda se triplica, pasando de 1 a 3. La forma del gráfico se conserva, pero queda dilatada verticalmente.
Contracción vertical
La contracción vertical se produce cuando el factor cumple $0 < n < 1$:
$$ y = n \cdot f(x) \quad \text{con } 0 < n < 1 $$
En este caso, la amplitud del gráfico de la función disminuye.
Ejemplo
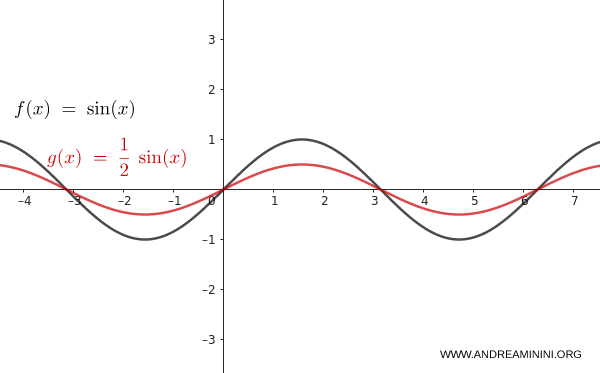
Tomemos $f(x) = \sin(x)$.
Aplicamos una contracción vertical con $n = \frac{1}{2}$:
$$ y = \dfrac{1}{2} \cdot \sin(x) $$
La amplitud se reduce de 1 a 0,5. El gráfico se contrae verticalmente hacia el eje $x$, mientras su forma general permanece inalterada.
Y así sucesivamente.