Codominio de una Función
El codominio de una función o relación $$ f:X \rightarrow Y $$ es el conjunto Y.
Al conjunto X se le llama dominio de la función.
El subconjunto del codominio formado por los valores que la función f efectivamente genera se denomina imagen de la función y se escribe Im(f).
$$ Im(f) \subseteq Y $$
En general, la imagen de una función no necesariamente coincide con su codominio.
Un ejemplo práctico
Tomemos dos conjuntos finitos, X e Y:
$$ X = \{1,2,3,4,5 \} $$
$$ Y = \{1,2,3,4,5,6,7,8,9 \} $$
y la relación
$$ f: y = x^2 $$
El codominio de esta relación es el conjunto Y:
$$ Y = \{1,2,3,4,5,6,7,8,9 \} $$
La imagen de la función es un subconjunto del codominio:
$$ Im(f) = \{1,4,9 \} \subseteq X $$
Son precisamente los elementos de Y que pueden escribirse como el cuadrado de algún elemento de X.
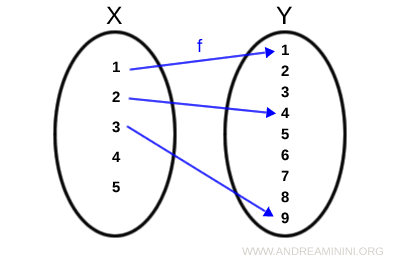
$$ f: 1^2 \mapsto 1 $$
$$ f: 2^2 \mapsto 4 $$
$$ f: 3^2 \mapsto 9 $$
Ejemplo 2
Consideremos ahora la función real
$$ f: y = \sin(x) $$
En este caso, tanto el dominio como el codominio son el conjunto de los números reales:
$$ f: \mathbb{R} \rightarrow \mathbb{R} $$
La función está definida en todos los números reales, de manera que el dominio coincide con todo el conjunto de los reales.
No obstante, la imagen no coincide con el codominio, ya que los valores de la función seno están siempre comprendidos en el intervalo [-1,1].
Y así sucesivamente.