Puntos de Acumulación

Consideremos un conjunto I de números reales. Un punto x₀ se denomina punto de acumulación de I si, para cualquier δ > 0, existe al menos un número real x en I tal que $$ 0 \ne |x - x_0| < \delta $$.

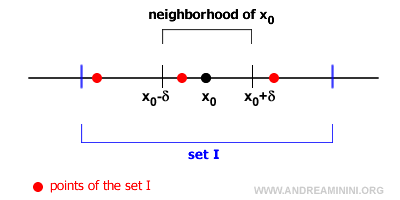
En otras palabras, si dentro del intervalo (x₀ - δ, x₀ + δ) existe al menos un punto de I distinto de x₀, entonces x₀ es un punto de acumulación de I.

Nota. Si el conjunto I está formado por un único punto [a,b] con a = b, entonces I no posee puntos de acumulación, ya que no existen otros puntos distintos a x₀ = a.

El caso de los intervalos cerrados y abiertos

Es importante diferenciar entre intervalos cerrados y abiertos:

• En un intervalo cerrado [a, b] con a < b, cada punto dentro de [a, b] es un punto de acumulación.
• En un intervalo abierto (a, b) con a < b, todos los puntos de (a, b) son de acumulación, y además los extremos a y b también lo son.

Por lo tanto, los puntos de acumulación de un intervalo abierto (a, b) coinciden con los del intervalo cerrado [a, b].

Infinitos números reales en el entorno

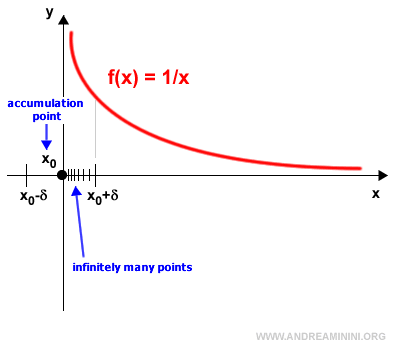
Si I es un subconjunto de los números reales R, $$ I \subseteq R $$ entonces el punto x₀ ∈ R es un punto de acumulación de I únicamente si en cualquier entorno (x₀ - δ, x₀ + δ) aparecen infinitos puntos de I distintos de x₀.

Demostración

Supongamos que x₀ es un punto de acumulación. Para alcanzar una contradicción, asumamos que en cierto entorno de radio δ > 0 existen únicamente un número finito de puntos de I, digamos k.

$$ | x_0 - x_i | < \delta \quad \forall i = 1, \dots, k $$

Definimos ahora δ₁ como la menor distancia entre x₀ y alguno de estos puntos:

$$ \delta_1 = \min | x_0 - x_i | \quad \forall i = 1, \dots, k $$

Entonces, en el entorno (x₀ - δ₁, x₀ + δ₁) no habría más puntos de I distintos de x₀.

$$ (x_0 - \delta_1, x_0 + \delta_1) $$

Esto contradice la hipótesis de que x₀ es un punto de acumulación.

Por lo tanto, si x₀ es un punto de acumulación en R, todo entorno de x₀ debe contener infinitos puntos de I.

Las sucesiones extraídas del entorno convergen al punto de acumulación

Si x₀ es un punto de acumulación de un conjunto I en R, entonces existe una sucesión de puntos x_n en I, todos distintos de x₀, que converge a x₀.

Demostración

Tomemos un número natural cualquiera n ∈ N para definir el radio del entorno δ:

$$ \delta = \frac{1}{n} $$

Así obtenemos un entorno de x₀:

$$ ( x_0 - \delta, \; x_0 + \delta ) $$

Como x₀ es un punto de acumulación, en este entorno hay infinitos puntos de I distintos de x₀.

$$ x_0 - \frac{1}{n} < x_n < x_0 + \frac{1}{n} $$

Esta desigualdad permite definir tres sucesiones de I para cada n ∈ N.

Analicemos ahora los límites de estas tres sucesiones cuando n tiende a infinito:

$$ \lim_{n \rightarrow \infty} \left(x_0 - \frac{1}{n}\right) < \lim_{n \rightarrow \infty} x_n < \lim_{n \rightarrow \infty} \left(x_0 + \frac{1}{n}\right) $$

Los límites de la primera y de la tercera sucesión convergen a x₀ cuando n → ∞:

$$ x_0 < \lim_{n \rightarrow \infty} x_n < x_0 $$

Por el Teorema del Sandwich, el límite de la sucesión intermedia también debe converger a x₀.

Con esto queda demostrada la proposición.

Dado un punto de acumulación x₀ del conjunto I, si toda sucesión x_n tomada de I \ {x₀} y convergente a x₀ genera una sucesión f(x_n) que converge a un cierto límite l, entonces la función f(x) tiene límite igual a l cuando x tiende a x₀. $$ \lim_{x \rightarrow x_0} f(x) = l $$

Ejemplo

Consideremos la función f(x) = x² + 1. El punto x₀ = 0 es un punto de acumulación respecto al conjunto I = (-1, 0).

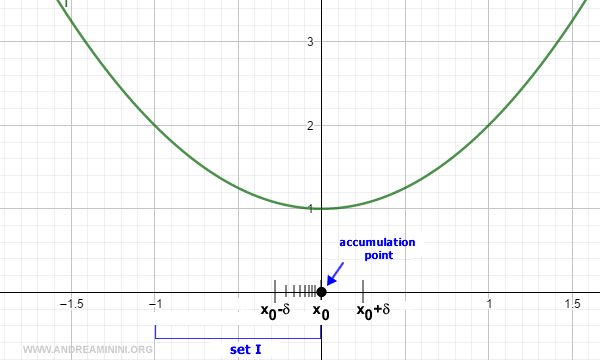
Para cualquier entorno (x₀ - δ, x₀ + δ), toda sucesión x_n tomada de I y que converge a x₀ produce una sucesión f(x_n) que converge a l = 1.

En consecuencia, el límite de la función cuando x → 0 es 1.

$$ \lim_{x \rightarrow 0} \; x^2 + 1 = 1 $$

El infinito como punto de acumulación

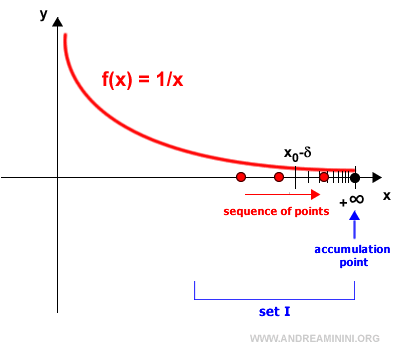
Un punto de acumulación también puede estar en el infinito (+∞ o -∞) para un conjunto I ⊆ R si existe al menos un punto de I en un entorno del infinito.

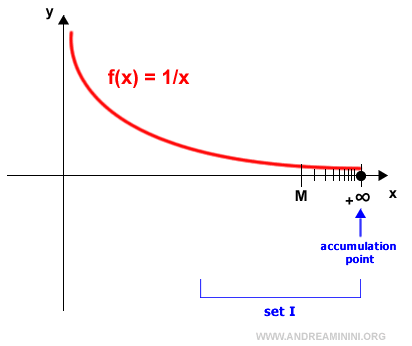
En este caso, el entorno del punto de acumulación x₀ es un intervalo de la forma (M, +∞) que contiene a todos los números reales x > M.

Desde luego, +∞ es un punto de acumulación únicamente si constituye la cota superior del conjunto I.

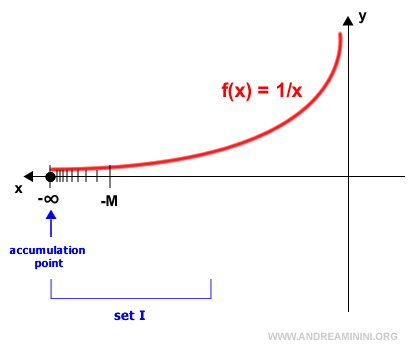
Nota. De manera análoga, lo mismo ocurre con el entorno (-∞, -M), para cualquier x < -M. En este caso, -∞ es un punto de acumulación solo si representa la cota inferior de I.

Y así sucesivamente.