Teorema de Bolzano

El Teorema de Bolzano, conocido también como teorema de la existencia de ceros, afirma algo muy simple pero profundo: si una función continua f(x) toma valores de signo opuesto en los extremos de un intervalo [a, b], entonces en algún punto intermedio la función se anula. En otras palabras, existe al menos un valor x₀ dentro del intervalo tal que f(x₀) = 0.

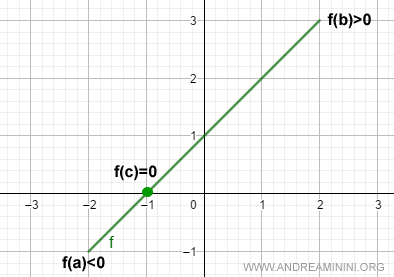
Este resultado también es válido si ocurre lo contrario, es decir, si f(a) > 0 y f(b) < 0. Lo esencial es que la función cambie de signo entre los dos extremos: f(a)·f(b) < 0.

Un ejemplo sencillo

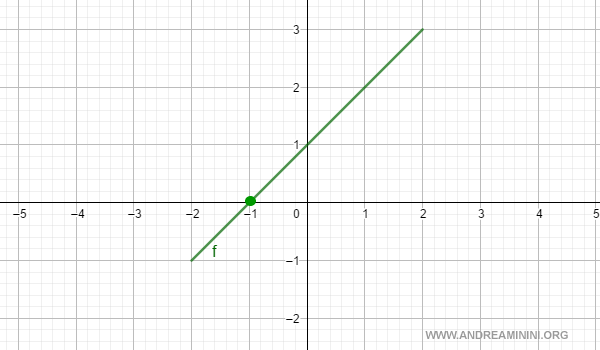
Veamos un caso fácil para entenderlo mejor. Tomemos la función:

$$ f(x) = x + 1 $$

definida en el intervalo cerrado [-2, 2].

En el punto x₀ = -1, la función se hace cero:

$$ f(-1) = 0 $$

Es un ejemplo muy simple, pero muestra claramente la idea: si en un extremo la función es negativa y en el otro positiva, en algún punto entre ambos debe pasar por cero.

Cómo se demuestra

Imaginemos una función continua f(x) definida en un intervalo [a, b], con f(a) < 0 y f(b) > 0. Por ser continua, la función no puede “saltar” de valores negativos a positivos sin pasar por cero. Esa es, de hecho, la intuición detrás del teorema.

Para verlo con más detalle, tomemos el punto medio del intervalo:

$$ c = \frac{a + b}{2} $$

Ejemplo. Volvamos al caso anterior: f(x) = x + 1 en [-2, 2]. En este intervalo, f(-2) = -1 y f(2) = 3. El punto medio es c = 0 y f(c) = 1.

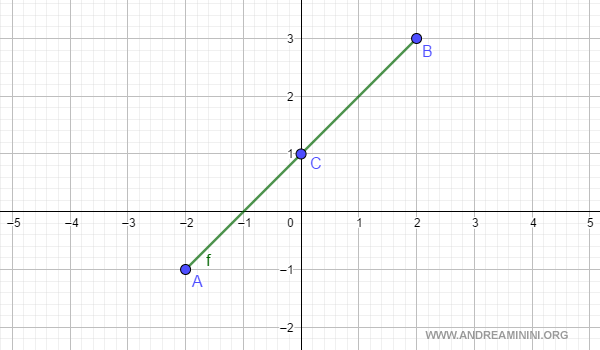
Ahora, observemos qué ocurre en c:

• Si f(c) > 0, la raíz debe estar entre a y c, porque f(a) < 0.
• Si f(c) < 0, la raíz está entre c y b, porque f(b) > 0.

Ejemplo. En nuestro caso, f(c) = 1, así que la raíz debe estar entre a = -2 y c = 0. Repetimos el proceso tomando el punto medio de este nuevo intervalo y seguimos reduciendo el rango paso a paso.

Con cada iteración el intervalo se hace más pequeño, y la función sigue cambiando de signo en sus extremos. Este procedimiento se repite hasta que la diferencia entre los extremos es tan pequeña que el valor de f(x) se aproxima a cero. En ese punto hemos encontrado, con la precisión deseada, una raíz de la función.

El razonamiento matemático

En cada paso del proceso los extremos del intervalo se van aproximando a un valor común. Podemos representarlos mediante tres sucesiones:

$$ a_n, \; b_n, \; c_n $$

Con cada iteración:

$$ b_n - a_n = \frac{b - a}{2^n} $$

De modo que la longitud del intervalo se reduce a la mitad en cada paso, tendiendo a cero cuando n tiende a infinito.

La sucesión {a_n} es creciente y está acotada superiormente, por lo que converge a un límite finito x₀:

$$ \lim_{n \rightarrow \infty} a_n = x_0 $$

La sucesión {b_n} se comporta de forma análoga y también converge al mismo límite:

$$ \lim_{n \rightarrow \infty} b_n = x_0 $$

Esto significa que ambas se acercan al mismo punto desde lados opuestos:

$$ a_n \le x_0 \le b_n $$

Si evaluamos la función en esos puntos, obtenemos:

$$ f(a_n) \le 0, \quad f(b_n) \ge 0 $$

y al tomar el límite cuando n → ∞, se cumple necesariamente:

$$ f(x_0) = 0 $$

Conclusión

El Teorema de Bolzano garantiza que toda función continua que cambie de signo en un intervalo tiene al menos una raíz dentro de él.  Más allá de su sencillez, este resultado es la base de muchos métodos numéricos, como el de bisección, y constituye una de las piedras angulares del análisis matemático.