El teorema de la conservación del signo en el límite de una sucesión

Cuando el límite de una sucesión a_n al crecer n tiende a un valor l mayor que cero, podemos afirmar que a partir de cierto punto todos los términos de la sucesión serán positivos. $$ \lim_{n \rightarrow \infty } a_n = l > 0 \; \rightarrow \; \exists \, v \; : \; \forall n > v, \; a_n > 0 $$

Un ejemplo para entenderlo mejor

Tomemos la sucesión:

$$ a_n = \frac{n-3}{n} $$

Si calculamos los primeros términos, obtenemos:

$$ a_1 = -2 \\ a_2 = -0.5 \\ a_3 = 0 \\ a_4 = 0.25 \\ a_5 = 0.4 \\ \vdots $$

El límite es claramente +1:

$$ \lim_{n \rightarrow \infty} \frac{n-3}{n} = 1 $$

Según el teorema, a partir de cierto índice v todos los términos mantienen el mismo signo que el límite. En este caso, los términos se vuelven positivos a partir de n = 4.

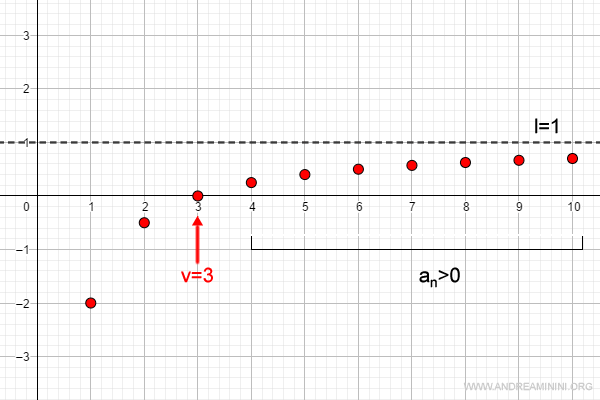
En concreto, v = 3, ya que para todo n > v los términos son positivos, coherentes con el signo del límite (1).

$$ a_4 = 0.25 \\ a_5 = 0.4 \\ \vdots $$

Nota. Este teorema no dice que todos los términos de la sucesión tengan el mismo signo que el límite, sino que a partir de cierto punto (n > v) esto ocurre. En el ejemplo, los dos primeros términos son negativos, el tercero es cero y, desde el cuarto en adelante, todos son positivos.

Cómo se demuestra

Partimos de que el límite l es positivo:

$$ \lim_{n \rightarrow \infty} a_n = l > 0 $$

Por definición de límite, existe un ε > 0 tal que:

$$ | a_n - l | < \epsilon $$

Si elegimos ε = l/2, obtenemos:

$$ | a_n - l | < \frac{l}{2} $$

Esto significa que, para todo n suficientemente grande, la diferencia entre a_n y l será menor que l/2. Reescribiendo:

$$ -\frac{l}{2} < a_n - l < \frac{l}{2} $$

Sumamos l a todos los términos:

$$ l - \frac{l}{2} < a_n < l + \frac{l}{2} $$

y simplificamos:

$$ \frac{l}{2} < a_n < \frac{3l}{2} $$

Como l > 0, su mitad también lo es, por lo que necesariamente:

$$ 0 < a_n $$

En otras palabras, todos los términos de la sucesión a partir de un cierto índice son positivos. Así se demuestra que el signo del límite se conserva en los términos sucesivos.

Corolarios interesantes

Corolario 1

Si todos los términos de una sucesión son no negativos, su límite también será no negativo: $$ \forall n > 0 : a_n \ge 0 \; \Rightarrow \; \lim_{n \rightarrow \infty} a_n = l \ge 0 $$

Y de forma análoga, si todos los términos son no positivos, el límite tampoco podrá ser positivo.

Demostración

Si todos los términos de la sucesión son mayores o iguales que cero, pero el límite fuese negativo, el teorema anterior implicaría que, a partir de cierto índice v, los términos también serían negativos, lo cual contradice la hipótesis inicial.

Por tanto, el límite no puede ser negativo. Debe cumplirse que l ≥ 0.

Corolario 2

Si dos sucesiones a_n y b_n convergen respectivamente a l_a y l_b, y se cumple que a_n ≥ b_n para todo n > 0, entonces sus límites también respetan esa relación: $$ \forall n > 0 : a_n \ge b_n \; \Rightarrow \; l_a \ge l_b $$

Demostración

Por hipótesis, cada término de a_n es mayor o igual que el correspondiente de b_n, por lo que:

$$ a_n - b_n \ge 0 $$

y, en consecuencia,

$$ \lim_{n \rightarrow \infty} (a_n - b_n) \ge 0 $$

Si el límite de la diferencia fuese negativo, según el teorema de la conservación del signo habría un punto a partir del cual a_n < b_n, lo que contradice la condición inicial.

Por tanto, el límite de la diferencia no puede ser negativo y debe cumplirse que l_a ≥ l_b.

Este resultado, sencillo pero poderoso, nos permite comparar límites a partir de desigualdades entre términos individuales de las sucesiones.