Criterio del Cociente para Sucesiones

Sea a_n una sucesión de términos positivos. Si la sucesión definida por b_n = a_n+1/a_n converge a un límite l_b con l_b < 1, entonces la sucesión a_n converge necesariamente a cero.

Un ejemplo práctico

Ejemplo 1

Partamos de la siguiente sucesión:

$$ a_n = \frac{n^2+1}{2^n} $$

Sus términos son positivos para todo n > 0, así que podemos aplicar directamente el criterio del cociente. Para ello definimos la sucesión de razones b_n:

$$ b_n = \frac{a_{n+1}}{a_n} = \frac{ \frac{(n+1)^2+1}{2^{n+1}} }{ \frac{n^2+1}{2^n} } = \frac{(n+1)^2+1}{2^{n+1}} \cdot \frac{2^n}{n^2+1} $$

$$ b_n = \frac{n^2+2n+1}{2 \cdot 2^n} \cdot \frac{2^n}{n^2+1 } = \frac{n^2+2n+1}{2n^2+2 } $$

Al analizar esta expresión observamos que el numerador y el denominador son polinomios del mismo grado. Esto simplifica el cálculo del límite, ya que basta con comparar los términos principales:

$$ \lim_{n \rightarrow ∞} b_n = \lim_{n \rightarrow ∞} \frac{n^2+2n+1}{2n^2+2} = \lim_{n \rightarrow ∞} \frac{n^2}{2n^2} = \frac{1}{2} < 1 $$

El resultado es claro: como el cociente tiende a un valor menor que 1, la sucesión original a_n debe converger a cero según el criterio del cociente:

$$ \lim_{n \rightarrow ∞} a_n = \lim_{n \rightarrow ∞} \frac{n^2+1}{2^n} = 0 $$

Esto significa que a_n es una sucesión infinitesimal. El crecimiento polinómico del numerador no puede compensar el crecimiento exponencial del denominador, que termina imponiéndose. La figura siguiente muestra de forma visual el comportamiento de ambas sucesiones:

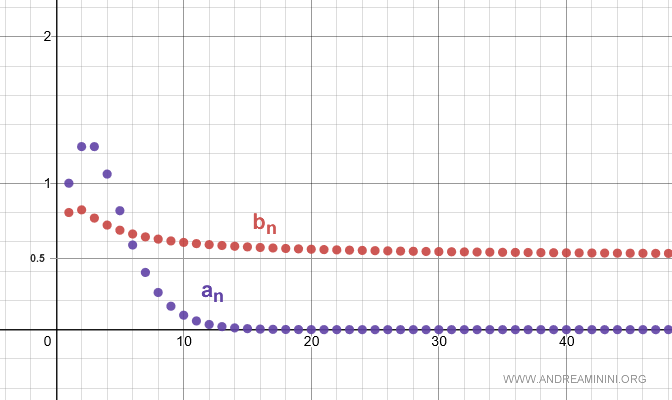
Demostración del criterio

Consideremos ahora una sucesión a_n de términos positivos y, además, monótona. Definimos la sucesión asociada:

$$ b_n = \frac{a_{n+1}}{a_n} $$

Supondremos que existe el límite de b_n y que su valor es estrictamente menor que 1:

$$ \lim_{n \rightarrow ∞} b_n < 1 $$

Esto implica que la diferencia (1 - b_n) tiene límite positivo:

$$ \lim_{n \rightarrow ∞} (1 - b_n) > 0 $$

Según el teorema de la permanencia del signo, a partir de cierto índice v se cumple que b_n permanece por debajo de 1:

$$ b_n = \frac{a_{n+1}}{a_n} < 1 $$

De esta desigualdad se obtiene que la sucesión es estrictamente decreciente:

$$ a_{n+1} < a_n $$

Nota. El límite de (1 - b_n) solo puede ser positivo si, más adelante, la razón b_n se mantiene por debajo de 1.

Al ser positiva y decreciente, la sucesión a_n es también acotada, ya que nunca puede hacerse negativa. Por el teorema de las sucesiones monótonas acotadas, debe converger a un límite finito:

$$ \lim_{n \rightarrow ∞} a_n = l_a \ge 0 $$

Solo existen dos posibilidades:

• l_a es estrictamente mayor que cero,
• o bien l_a es igual a cero.

Si el límite fuera mayor que cero, entonces:

$$ \lim_{n \rightarrow ∞} b_n = \frac{l_a}{l_a} = 1 $$

Esto contradice nuestra hipótesis inicial, ya que b_n debía permanecer por debajo de 1. Por tanto, la única conclusión posible es:

$$ \lim_{n \rightarrow ∞} a_n = 0 $$

Con esto queda demostrada la validez del criterio.