Formas Indeterminadas en los Límites
Al calcular límites, con frecuencia aparecen formas indeterminadas: situaciones en las que el resultado no es evidente de inmediato y exige un análisis más detallado. Estas son las formas indeterminadas más habituales en problemas de límites:
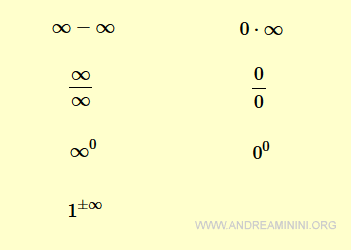
El hecho de que un límite adopte una forma indeterminada no implica que el límite no exista.
Para evaluarlo, es necesario reescribir o simplificar la expresión de modo que desaparezca la indeterminación.
Cómo resolver una forma indeterminada
Cuando un límite presenta una forma indeterminada, no es posible calcularlo mediante una sustitución directa. En estos casos es necesario transformar la expresión para entender cuál es realmente el comportamiento de la función.
En el análisis matemático se utilizan varias estrategias para resolver este tipo de límites.
- Manipulación algebraica. En muchos casos basta con realizar algunas transformaciones algebraicas para eliminar la indeterminación. Reescribir la expresión en una forma equivalente puede simplificar el cálculo del límite. Sin embargo, este método no siempre es inmediato y en algunos problemas no existe una transformación sencilla.
- Límites notables. Algunos límites que generan formas indeterminadas pueden resolverse utilizando los límites notables estudiados en análisis matemático. En estos casos, la expresión del límite se transforma hasta que puede reducirse a uno de los límites fundamentales conocidos.
- Desarrollos en serie de Taylor. Otra técnica consiste en sustituir funciones exponenciales, logarítmicas o trigonométricas por sus desarrollos en serie de Taylor. De esta forma, las funciones se aproximan mediante polinomios que describen su comportamiento local.
- Regla de L'Hôpital. Si la función es derivable y la forma indeterminada es \(0/0\) o \(\infty/\infty\), se puede aplicar la regla de L'Hôpital. Esta regla consiste en estudiar el límite de las derivadas del numerador y del denominador. El procedimiento puede repetirse varias veces, tomando sucesivamente derivadas, hasta que el límite deje de ser indeterminado y adopte un valor finito o infinito. En la práctica, la regla de L'Hôpital se utiliza con frecuencia cuando intervienen funciones logarítmicas, exponenciales o trigonométricas.
Ejemplo. Este límite presenta la forma indeterminada \(\infty/\infty\) $$ \lim_{x \rightarrow \infty} \frac{e^x}{x} = \frac{\infty}{\infty} $$ Aplicamos la regla de L'Hôpital y calculamos las derivadas del numerador y del denominador $$ \lim_{x \rightarrow \infty} \frac{D[e^x]}{D[x]} = \lim_{x \rightarrow \infty} \frac{e^x}{1} = + \infty $$ Por lo tanto, el límite diverge.
Ejemplo 1. Este límite presenta una forma indeterminada del tipo \(0/0\): $$ \lim_{n \rightarrow \infty} \ \frac{\frac{1}{n^2}}{\frac{1}{n}} = \frac{0}{0} $$ Si simplificamos la expresión algebraicamente, la indeterminación desaparece: $$ \lim_{n \rightarrow \infty} \frac{1}{n^2} \cdot \frac{n}{1} = \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$
Multiplicación por el conjugado
En algunos límites aparece una diferencia entre dos términos que contienen una raíz cuadrada. Cuando esto ocurre, es frecuente que la expresión produzca una forma indeterminada del tipo \(+\infty - \infty \).
En estas situaciones conviene aplicar una técnica algebraica muy utilizada en cálculo: multiplicar por el conjugado. Este procedimiento permite transformar la expresión y eliminar la raíz cuadrada que dificulta el análisis del límite.
La idea es sencilla. Se multiplica y se divide la expresión por el conjugado, es decir, por la misma expresión pero con el signo opuesto entre los términos. De este modo se puede aplicar la identidad algebraica
\( (a-b)(a+b)=a^2-b^2 \)
Esta identidad convierte el producto en una diferencia de cuadrados, lo que elimina la raíz cuadrada y simplifica notablemente la expresión.
Ejemplo
Consideremos el siguiente límite cuando $ x \to \infty $, donde aparece una diferencia entre dos términos que incluyen una raíz cuadrada:
\[ \lim_{x \to \infty} x-\sqrt{x^2+1} \]
Si analizamos el comportamiento de cada término cuando \(x\) crece sin límite, vemos que ambos tienden a \(+\infty\). Por lo tanto la expresión produce una forma indeterminada del tipo \(+\infty - \infty\).
\[ \lim_{x \to \infty} x-\sqrt{x^2+1} = +\infty - \infty \]
Para resolver el límite multiplicamos y dividimos por el conjugado de \(x-\sqrt{x^2+1}\), es decir \(x+\sqrt{x^2+1}\).
\[ x-\sqrt{x^2+1} = x-\sqrt{x^2+1} \cdot \frac{x+\sqrt{x^2+1}}{x+\sqrt{x^2+1} } \]
El producto \((x-\sqrt{x^2+1})(x+\sqrt{x^2+1})\) es una diferencia de cuadrados:
\[ x^2-(\sqrt{x^2+1})^2 \]
Por lo tanto la expresión puede escribirse de forma equivalente como
\[ \frac{x^2-(\sqrt{x^2+1})^2}{x+\sqrt{x^2+1} } \]
En el numerador la raíz cuadrada desaparece:
\[ \frac{x^2-(x^2+1)}{x+\sqrt{x^2+1} } \]
\[ \frac{-1}{x+\sqrt{x^2+1} } \]
Ahora la expresión es mucho más sencilla de estudiar.
Cuando \(x \to \infty\), el denominador crece sin límite. Por lo tanto la fracción tiende a cero.
\[ \lim_{x \to \infty} \frac{-1}{x+\sqrt{x^2+1} } = 0 \]
En consecuencia, también el límite original es igual a cero:
\[ \lim_{x \to \infty} x-\sqrt{x^2+1} = \lim_{x \to \infty} \frac{-1}{x+\sqrt{x^2+1} } = 0 \]
Este ejemplo muestra cómo la multiplicación por el conjugado permite transformar una expresión con raíces en una forma más simple. Por esta razón es una técnica algebraica muy útil para calcular límites que contienen diferencias entre expresiones con raíces cuadradas.
Factorizar la mayor potencia de \(x\)
Al estudiar el límite de una función polinómica cuando \( x \to +\infty \) o \( x \to -\infty \), es frecuente que la expresión adopte la forma indeterminada \( \infty - \infty \).
\[ \lim_{x \to +\infty \atop (x \to -\infty)} \left( a_0 x^n + a_1 x^{n-1} + \dots + a_n \right) = \infty - \infty \]
Para resolver esta indeterminación, resulta útil factorizar la mayor potencia de \( x \) presente en el polinomio.
\[ \lim_{x \to +\infty \atop (x \to -\infty)} x^n \left( a_0 + \frac{a_1}{x} + \frac{a_2}{x^2} + \dots + \frac{a_n}{x^n} \right) \]
De este modo, el polinomio se escribe como el producto de \( x^n \) por una expresión que contiene términos como \( \frac{a_1}{x}, \frac{a_2}{x^2}, \dots \).
Cuando \( x \to \pm \infty \), todos esos términos fraccionarios tienden a \( 0 \). En consecuencia, la expresión entre paréntesis tiende al coeficiente del término de mayor grado.
Por esta razón, el comportamiento del límite queda determinado por el término dominante \( a_0 x^n \), que permite establecer si el límite diverge hacia \( +\infty \) o hacia \( -\infty \).
\[ \lim_{x \to +\infty \atop (x \to -\infty)} \left( a_0 x^n + a_1 x^{n-1} + \dots + a_n \right) = \lim_{x \to +\infty \atop (x \to -\infty)} a_0 x^n \]
El signo del límite se determina aplicando las reglas habituales de los signos al producto \( a_0 x^n \).
Ejemplo
Consideremos el siguiente límite
\[ \lim_{x \to +\infty} (3x^2 - 5x + 1) \]
Para eliminar la forma indeterminada, factorizamos la mayor potencia de \( x \), que en este caso es \( x^2 \):
\[ 3x^2 - 5x + 1 = x^2 \left(3 - \frac{5}{x} + \frac{1}{x^2}\right) \]
El límite se convierte entonces en
\[ \lim_{x \to +\infty} x^2 \left(3 - \frac{5}{x} + \frac{1}{x^2}\right) \]
Cuando \( x \to \infty \), los términos \( \frac{5}{x} \) y \( \frac{1}{x^2} \) tienden a cero. Por lo tanto, la expresión entre paréntesis tiende a \( 3 \), y el comportamiento del límite queda determinado por el término dominante \( 3x^2 \).
\[ \lim_{x \to +\infty} x^2 \left(3 - \frac{5}{x} + \frac{1}{x^2}\right) = \lim_{x \to +\infty} 3x^2 = +\infty \]
En consecuencia, el límite original también diverge:
\[ \lim_{x \to +\infty} (3x^2 - 5x + 1) = +\infty \]
Esta técnica permite resolver fácilmente las formas indeterminadas \( \infty - \infty \) que aparecen en los límites de funciones polinómicas cuando \( x \to \pm \infty \).
Nota. En muchos límites de funciones polinómicas cuando \( x \to \pm\infty \), ni siquiera es necesario realizar todos los pasos intermedios. A medida que \( x \) crece en valor absoluto, los términos de menor grado se vuelven insignificantes frente al término de mayor grado. Por esta razón, un polinomio es asintóticamente equivalente a su término dominante \( a_0 x^n \). En consecuencia, el comportamiento del límite coincide con el de \( a_0 x^n \). Por ejemplo, el ejercicio anterior podría resolverse directamente así: \[ \lim_{x \to +\infty} (3x^2 - 5x + 1) = \lim_{x \to +\infty} 3x^2 = +\infty \]
Límites con indeterminación \( 0 \cdot \infty \)
La indeterminación \( 0 \cdot \infty \) aparece en un límite cuando uno de los factores tiende a cero mientras el otro crece sin límite.
\[ \lim_{x \to a} f(x) g(x) = 0 \cdot \infty \]
A primera vista podría pensarse que el resultado es cero o infinito. Sin embargo, no es posible determinar el valor del límite de manera directa. El resultado depende de la velocidad con la que cada factor se aproxima a \( 0 \) y a \( \infty \).
Para estudiar este tipo de límite, la técnica más utilizada consiste en transformar el producto en un cociente. De esta forma el límite puede convertirse en una indeterminación más fácil de analizar.
\[ f(x) g(x) = \frac{f(x)}{\frac{1}{g(x)}} \]
o bien
\[ f(x) g(x) = \frac{g(x)}{\frac{1}{f(x)}} \]
Después de esta transformación, el límite suele adoptar una de las formas indeterminadas más comunes:
\( \frac{0}{0} \) o \( \frac{\infty}{\infty} \)
Estas formas pueden estudiarse con las técnicas habituales del cálculo.
Ejemplo
Consideremos el siguiente límite:
\[ \lim_{x \to +\infty} x e^{-x} \]
En este caso aparece la indeterminación \( 0 \cdot \infty \), porque
\( x \to \infty \)
mientras que
\( e^{-x} \to 0 \)
Por lo tanto:
\[ \lim_{x \to +\infty} x e^{-x} = 0 \cdot \infty \]
Para resolver el límite, reescribimos el producto como un cociente:
\[ x e^{-x} = \frac{x}{e^{x}} \]
El límite se convierte entonces en:
\[ \lim_{x \to +\infty} \frac{x}{e^{x}} = \frac{\infty}{\infty} \]
Sabemos que la función exponencial crece mucho más rápido que cualquier polinomio. Por esta razón, el denominador domina al numerador cuando \( x \to \infty \).
En consecuencia:
\[ \lim_{x \to +\infty} \frac{x}{e^{x}} = 0 \]
En resumen, cuando aparece la indeterminación \( 0 \cdot \infty \), el paso clave consiste en transformar el producto en un cociente. Esta sencilla manipulación permite convertir el límite en una forma indeterminada más manejable y analizarlo con los métodos habituales del cálculo.
Límites con la forma indeterminada \( \frac{\infty}{\infty} \)
Un límite presenta la forma indeterminada \( \frac{\infty}{\infty} \) cuando tanto el numerador como el denominador divergen mientras la variable se aproxima a un determinado valor, normalmente \( x \to \infty \) o \( x \to -\infty \).
En estos casos no es posible calcular el límite mediante sustitución directa. Primero hay que transformar o simplificar la expresión para entender cuál es su comportamiento.
Para resolver este tipo de límites se utilizan principalmente tres técnicas.
1] Factorizar la mayor potencia
Este es el método más simple cuando la expresión está formada por polinomios. La idea consiste en factorizar la mayor potencia de la variable tanto en el numerador como en el denominador.
Ejemplo
\[ \lim_{x \to \infty} \frac{3x^2 - 5x + 1}{2x^2 + x} \]
Factorizamos la mayor potencia \( x^2 \)
\[ \frac{x^2\left(3 - \frac{5}{x} + \frac{1}{x^2}\right)}{x^2\left(2 + \frac{1}{x}\right)} \]
Luego simplificamos \( x^2 \)
\[ \frac{3 - \frac{5}{x} + \frac{1}{x^2}}{2 + \frac{1}{x}} \]
Cuando \( x \to \infty \), los términos \( \frac{5}{x} \) y \( \frac{1}{x^2} \) tienden a cero.
\[ \lim_{x \to \infty} \frac{3x^2 - 5x + 1}{2x^2 + x} = \frac{3}{2} \]
En la práctica, el comportamiento del límite está determinado por los términos de mayor grado.
Nota. Si en el límite aparecen únicamente polinomios, normalmente no es necesario realizar todos los pasos intermedios. El valor del límite depende solo de la relación entre los términos de mayor grado. En otras palabras, basta con comparar los grados de los polinomios. \[ \lim_{x \to \pm \infty}
\frac{a_0 x^n + a_1 x^{n-1} + \dots + a_n} {b_0 x^m + b_1 x^{m-1} + \dots + b_m} = \begin{cases} \pm \infty & \text{si } n > m \\ \\ \dfrac{a_0}{b_0} & \text{si } n = m \\ \\ 0 & \text{si } n < m \end{cases} \] Por ejemplo, consideremos el límite \[ \lim_{x \to \infty} \frac{5x^4 + x}{2x^4 - 3x^2} \] El comportamiento de la función viene determinado por la relación entre los términos dominantes \(\frac{5x^4}{2x^4}\), por lo que el límite tiende a \( \frac{5}{2} \). \[ \lim_{x \to \infty} \frac{5x^4 + x}{2x^4 - 3x^2} = \frac{5}{2} \]
2] Dividir por la mayor potencia
Este método se basa en la misma idea que el anterior, pero se aplica dividiendo cada término de la expresión por la mayor potencia de la variable.
Por ejemplo, consideremos el siguiente límite
\[ \lim_{x \to \infty} \frac{4x^3 + x}{2x^3 - 5} \]
Dividimos todos los términos del numerador y del denominador por \( x^3 \)
\[ \lim_{x \to \infty} \frac{4 + \frac{1}{x^2}}{2 - \frac{5}{x^3}} \]
Cuando \( x \to \infty \), los términos \( \frac{1}{x^2} \) y \( \frac{5}{x^3} \) tienden a cero.
Por lo tanto, el límite es
\[ \lim_{x \to \infty} \frac{4 + \frac{1}{x^2}}{2 - \frac{5}{x^3}} = \frac{4}{2} = 2 \]
3] Regla de L'Hôpital
Si el límite incluye funciones más complejas, como logaritmos, exponenciales o funciones trigonométricas, puede aplicarse la regla de L'Hôpital.
Por ejemplo, consideremos el límite
\[ \lim_{x \to \infty} \frac{\ln x}{x} = \frac{\infty}{\infty} \]
Derivamos el numerador y el denominador
\[ \lim_{x \to \infty} \frac{D[\ln x]}{D[x]} \]
Sabemos que \( D[\ln x] = \frac{1}{x} \) y que \( D[x] = 1 \), por lo que sustituimos estos resultados
\[ \lim_{x \to \infty} \frac{\frac{1}{x}}{1} \]
\[ \lim_{x \to \infty} \frac{1}{x} = 0 \]
Por lo tanto, el límite de la función original también es cero.
\[ \lim_{x \to \infty} \frac{\ln x}{x} = 0 \]
Nota. Además de los tres métodos descritos, existen otras técnicas que pueden resultar útiles dependiendo de la forma de la expresión. Por ejemplo, se pueden utilizar límites notables cuando aparecen funciones trigonométricas, logarítmicas o exponenciales. En otros casos conviene aplicar transformaciones algebraicas, como factorizar, extraer factores comunes o racionalizar la expresión. A veces también es suficiente identificar los términos dominantes de la función para determinar el comportamiento del límite. El método más adecuado depende siempre de la estructura de la expresión y de las funciones que intervienen en el límite.
Formas Determinadas
No toda aparición de ceros o infinitos en un límite genera una forma indeterminada.
Por ejemplo, las siguientes expresiones no son indeterminadas:
| $$ k + \infty = +\infty $$ | Un número real k sumado con infinito |
| $$ k - \infty = -\infty $$ | Un número real k menos infinito |
| $$ \infty+\infty = \infty $$ | Infinito más infinito |
| $$ k \cdot \infty = \infty $$ | Una constante distinta de cero multiplicada por infinito |
| $$ \infty \cdot \infty = \infty $$ | Infinito por infinito |
| $$ \frac{k}{\infty} = 0 $$ | Una constante k dividida entre infinito |
| $$ \frac{0}{\infty} = 0 $$ | Cero dividido entre infinito |
| $$ \frac{\infty}{k} = \infty $$ | Infinito dividido entre una constante no nula k |
| $$ \frac{k}{0} = \infty $$ | Una constante no nula k dividida entre cero |
En estos casos, el resultado está bien definido desde el punto de vista algebraico. No se consideran formas indeterminadas.
Y así sucesivamente.