Teorema del Valor Intermedio

Cuando una función f(x) es continua en un intervalo cerrado [a, b], no puede "saltar" valores. Está obligada a recorrer todo lo que hay entre f(a) y f(b). A este resultado se le conoce como el Teorema de los Valores Intermedios.

Es uno de los pilares del análisis real. Nos dice que, siempre que una función no presente discontinuidades, cualquier valor intermedio entre sus valores extremos aparece necesariamente en algún punto del intervalo.

Un ejemplo para entenderlo

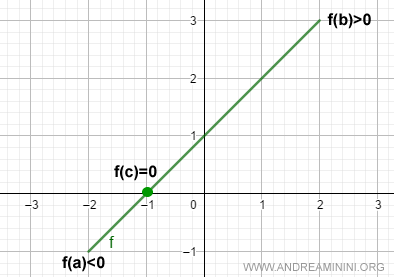
Miremos una función continua sencilla en el intervalo [-2, 2]:

$$ f(x) = x + 1 $$

Evaluémosla en los extremos:

$$ f(-2) = -1 \qquad f(2) = 3 $$

Aquí ocurre algo importante. La función pasa de un valor negativo a uno positivo, sin interrupciones. Eso significa que, a medida que avanzamos de x = -2 a x = 2, la función atraviesa todos los valores entre -1 y 3.

Este comportamiento no depende de la forma concreta de la función, sino únicamente de su continuidad. Este es precisamente el corazón del teorema.

Cómo se demuestra

Supongamos que f es continua y que f(a) ≤ f(b). El teorema afirma:

$$ \forall\, y_0 \in [f(a), f(b)],\ \exists\, x_0 \in [a, b] \ \text{tal que}\ f(x_0) = y_0 $$

Para justificar esto, introducimos una función auxiliar:

$$ g(x) = f(x) - y_0 $$

que mide cuánto se aleja f(x) del valor que nos interesa.

Evaluemos g(x) en los extremos:

$$ g(a) = f(a) - y_0 $$

$$ g(b) = f(b) - y_0 $$

Si y₀ está entre f(a) y f(b), entonces g(a) es negativa y g(b) es positiva:

$$ g(a) < 0 \qquad g(b) > 0 $$

Es decir, g(x) cambia de signo en el intervalo. Para funciones continuas, un cambio de signo implica que existe un punto donde la función cruza el cero. Esto es exactamente lo que garantiza el Teorema de Bolzano.

Por tanto, existe un x₀ tal que:

$$ g(x_0) = 0 \quad \Rightarrow \quad f(x_0) = y_0 $$

Así queda demostrada la idea principal: la continuidad obliga a la función a pasar por todos los valores intermedios.

Un corolario útil

Si una función es continua en [a, b], también adopta todos los valores comprendidos entre su mínimo m y su máximo M.

Cómo se demuestra

El Teorema de Weierstrass garantiza que una función continua alcanza su mínimo y máximo en el intervalo. Sea:

$$ m = f(x_1), \qquad M = f(x_2) $$

Tomemos cualquier valor y₀ entre m y M. Observemos la función:

$$ h(x) = f(x) - y_0 $$

En el punto donde f alcanza el mínimo tenemos:

$$ h(x_1) < 0 $$

En el punto donde alcanza el máximo:

$$ h(x_2) > 0 $$

h(x) también cambia de signo. Por Bolzano, existe un x₀ tal que:

$$ h(x_0) = 0 \quad \Rightarrow \quad f(x_0) = y_0 $$

Esto muestra que la función recorre todo el intervalo de valores entre m y M, sin omitir ninguno.

Y con ello queda completada la idea esencial detrás del Teorema del Valor Intermedio.