Ejercicios sobre límites de funciones de dos variables

Selección de ejercicios resueltos que ilustran el cálculo de límites en funciones de dos variables.

Ejercicio 1

Calculemos el siguiente límite:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} $$

Al aproximarse \((x, y)\) a \((0, 0)\), la expresión adopta la forma indeterminada \( \tfrac{0}{0} \):

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} = \frac{0}{0} $$

Para resolverlo introducimos un cambio de variable:

$$ t = x^2 + y^2 $$

Con esta sustitución, el límite en dos variables se reduce a un límite de una sola variable, bien conocido:

$$ \lim_{t \rightarrow 0} \frac{\sin(t)}{t} $$

Sabemos que:

$$ \lim_{t \rightarrow 0} \frac{\sin(t)}{t} = 1 $$

En consecuencia, el límite de la función original también es 1:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{\sin(x^2+y^2)}{x^2+y^2} = 1 $$

Ejercicio 2

Estudiemos ahora el límite de la función \( f(x,y) \):

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} $$

De nuevo aparece una indeterminación \(0/0\):

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} = \frac{0}{0} $$

Para analizarlo, conviene acotar la función utilizando su valor absoluto.

Nota. Para cualquier función \( f(x,y) \) se cumple: $$ -| f(x,y) | \le f(x,y) \le | f(x,y) |. $$ Si el límite de \( |f(x,y)| \) es cero, entonces, por el teorema del encajonamiento, también lo es el de \( f(x,y) \).

Consideremos el valor absoluto:

$$ \lim_{(x,y) \rightarrow (0,0)} \left| \frac{x^2y}{x^2+y^2} \right| $$

Es inmediato que:

$$ 0 \le \left| \frac{x^2y}{x^2+y^2} \right| $$

Podemos reescribir la expresión como:

$$ |y| \cdot \frac{x^2}{x^2+y^2} $$

El factor \( \frac{x^2}{x^2+y^2} \) está siempre entre 0 y 1, ya que el denominador es mayor o igual que el numerador.

Por tanto, la función está acotada superiormente por \( |y| \):

$$ 0 \le |y| \cdot \frac{x^2}{x^2+y^2} \le |y| $$

Al tomar límites:

$$ 0 \le \lim_{(x,y) \rightarrow (0,0)} |y| \cdot \frac{x^2}{x^2+y^2} \le \lim_{(x,y) \rightarrow (0,0)} |y| $$

Como los extremos tienden a 0, también lo hace el límite intermedio:

$$ \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{x^2+y^2} = 0 $$

Enfoque alternativo con coordenadas polares

Otra manera de resolverlo consiste en cambiar a coordenadas polares:

\[ x = \rho \cos \theta, \quad y = \rho \sin \theta \]

con \(\rho = \sqrt{x^2 + y^2}\) y \(\theta\) el ángulo respecto al eje \(x\).

Sustituyendo en la función:

\[ \frac{x^2 y}{x^2 + y^2} = \frac{(\rho \cos\theta)^2 (\rho \sin\theta)}{(\rho \cos\theta)^2 + (\rho \sin\theta)^2} \]

\[ = \frac{\rho^3 \cos^2\theta \sin\theta}{\rho^2(\cos^2\theta + \sin^2\theta)} \]

Por la identidad pitagórica, \(\cos^2\theta + \sin^2\theta = 1\), de modo que queda:

\[ \frac{x^2 y}{x^2 + y^2} = \rho \cos^2\theta \sin\theta \]

Al tomar el límite:

\[ \lim_{\rho \to 0} \rho \cos^2\theta \sin\theta = 0 \]

Así, ambos enfoques conducen a la misma conclusión:

\[ \lim_{(x,y)\to(0,0)} \frac{x^2 y}{x^2 + y^2} = 0 \]

Ejercicio 3

En este ejercicio analizamos el límite de la siguiente función de dos variables:

\[ \lim_{(x,y)\to(0,0)} \frac{xy}{x^2 + y^2} \]

El objetivo es determinar si dicho límite existe y, en caso afirmativo, cuál es su valor.

Observemos que el numerador \(xy\) puede ser positivo, negativo o nulo, mientras que el denominador es siempre positivo, pues \(x^2 + y^2 > 0\) siempre que \((x,y) \ne (0,0)\).

\[ f(x,y) = \frac{xy}{x^2 + y^2} \]

Por lo tanto, la función está definida en todo \(\mathbb{R}^2\) salvo en el origen \((0,0)\).

Solución 1

Una estrategia clásica para comprobar la existencia de un límite consiste en evaluarlo a lo largo de trayectorias distintas que convergen al punto. Si los resultados no coinciden, el límite no existe.

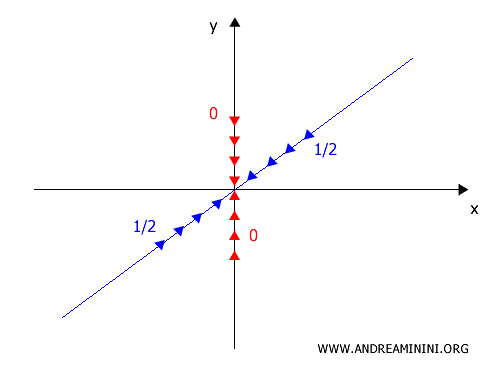
A] Caso 1: sobre la recta \(y = 0\)

Si fijamos \(y = 0\):

\[ f(x,0) = \frac{x \cdot 0}{x^2 + 0} = 0 \]

De modo que, sobre esta trayectoria, el límite es:

\[ \lim_{x \to 0} f(x,0) = 0 \]

B] Caso 2: sobre la recta \(y = x\)

Si sustituimos \(y = x\):

\[ f(x,x) = \frac{x \cdot x}{x^2 + x^2} = \frac{x^2}{2x^2} = \frac{1}{2} \]

Por tanto, en este caso:

\[ \lim_{x \to 0} f(x,x) = \tfrac{1}{2} \]

Las dos trayectorias conducen a resultados distintos:

• sobre \(y = 0\) → \(0\)
• sobre \(y = x\) → \(\tfrac{1}{2}\)

En consecuencia, el límite no existe.

Solución 2

Dado que el límite se toma en el origen, un enfoque igualmente eficaz es recurrir a coordenadas polares:

\[ x = \rho \cos\theta, \quad y = \rho \sin\theta \]

Nota. Las coordenadas polares resultan especialmente útiles al estudiar límites en el origen \((0,0)\). Si el punto de interés es distinto, basta trasladar el sistema de referencia para situarlo como nuevo origen.

Sustituyendo en la función:

\[ f(x,y) = \frac{(\rho \cos\theta)(\rho \sin\theta)}{(\rho \cos\theta)^2 + (\rho \sin\theta)^2} \]

\[ = \frac{\rho^2 \cos\theta \sin\theta}{\rho^2(\cos^2\theta + \sin^2\theta)} \]

\[ = \frac{\rho^2 \cos\theta \sin\theta}{\rho^2 \cdot 1} \]

\[ = \cos\theta \sin\theta \]

El límite se reduce entonces a:

\[ \lim_{\rho \to 0} f(x,y) = \cos\theta \sin\theta \]

El resultado no depende de \(\rho\), sino únicamente del ángulo \(\theta\), es decir, de la dirección de aproximación. Por tanto, el valor del límite varía con la trayectoria, lo que confirma que el límite no existe.

Ejercicio 4

Analizamos ahora el límite de la siguiente función de dos variables cuando \((x,y)\) tiende al origen \((0,0)\):

\[ \lim_{(x,y)\to(0,0)} \frac{xy^2}{x^2 + y^4} \]

La función está dada por:

\[ f(x,y) = \frac{xy^2}{x^2 + y^4} \]

El numerador \(xy^2\) se anula claramente al aproximarse \((x,y)\) al origen. El denominador, en cambio, es siempre positivo salvo en \((0,0)\), donde se anula, lo que hace que la función no esté definida en ese punto.

De este modo, el límite adopta la forma indeterminada \(\tfrac{0}{0}\), y requiere un análisis más detallado.

Solución 1

Examinemos el límite a lo largo de distintas trayectorias.

A] Caso 1: sobre la recta \(x = 0\)

Si fijamos \(x = 0\):

\[ f(0,y) = \frac{0 \cdot y^2}{0 + y^4} = 0 \]

Por tanto, en este camino el límite vale:

\[ \lim_{(x,y)\to(0,0)} f(0,y) = 0 \]

B] Caso 2: sobre la recta \(y = 0\)

Si fijamos \(y = 0\):

\[ f(x,0) = \frac{x \cdot 0}{x^2 + 0} = 0 \]

De nuevo, el límite es nulo:

\[ \lim_{(x,y)\to(0,0)} f(x,0) = 0 \]

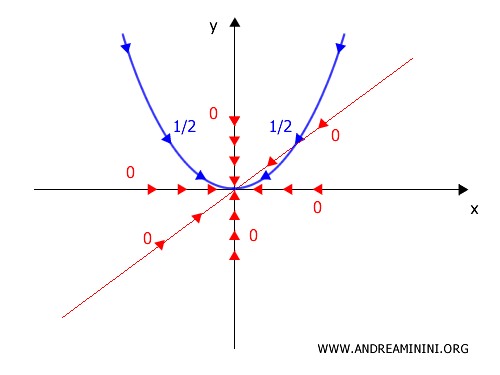
C] Caso 3: sobre la diagonal \(y = x\)

Si sustituimos \(y = x\):

\[ f(x,x) = \frac{x \cdot x^2}{x^2 + x^4} = \frac{x}{1+x^2} \]

Y al hacer \(x \to 0\):

\[ \lim_{x \to 0} \frac{x}{1+x^2} = 0 \]

D] Caso 4: sobre la parábola \(x = y^2\)

Si tomamos \(x = y^2\):

\[ f(y^2, y) = \frac{y^4}{2y^4} = \tfrac{1}{2} \]

En este caso, el límite es distinto:

\[ \lim_{(x,y)\to(0,0)} f(y^2,y) = \tfrac{1}{2} \]

Hemos hallado trayectorias que conducen a valores diferentes. En consecuencia, el límite global no existe.

Solución 2

Dado que el límite se toma en el origen, resulta natural recurrir a coordenadas polares:

\[ \lim_{(x,y)\to(0,0)} \frac{xy^2}{x^2 + y^4} \]

Con el cambio \(x = \rho \cos \theta, \ y = \rho \sin \theta\):

\[ \frac{(\rho \cos \theta)(\rho \sin \theta)^2}{(\rho \cos \theta)^2 + (\rho \sin \theta)^4} = \frac{\rho \cos \theta \cdot \rho^2 \sin^2 \theta}{\rho^2 \cos^2 \theta + \rho^4 \sin^4 \theta} \]

\[ = \rho \cdot \frac{\cos \theta \sin^2 \theta}{\cos^2 \theta + \rho^2 \sin^4 \theta} \]

Si mantenemos \(\theta\) constante (trayectorias rectas), el límite es siempre 0:

\[ \lim_{\rho \to 0} \rho \cdot \frac{\cos \theta \sin^2 \theta}{\cos^2 \theta + \rho^2 \sin^4 \theta} = 0 \]

Nota. Esto se debe a que el cociente \(\tfrac{\cos \theta \sin^2 \theta}{\cos^2 \theta + \rho^2 \sin^4 \theta}\) permanece acotado al tender \(\rho \to 0\). El factor \(\rho\) fuerza el valor total a cero.

Sin embargo, a lo largo de trayectorias curvas el resultado cambia. Supongamos, por ejemplo, que \(\cos \theta(\rho) = k \rho\) con \(k \ne 0\). Entonces:

\[ \lim_{\rho \to 0} \rho \cdot \frac{(k \rho)\cdot \sin^2 \theta}{(k \rho)^2 + \rho^2 \sin^4 \theta} \]

Como \(\sin^2 \theta(\rho) \to 1\) cuando \(\rho \to 0\), se obtiene:

\[ \lim_{\rho \to 0} \frac{k}{k^2+1} \]

Es decir, sobre ciertas trayectorias curvas el límite converge a un valor finito distinto de cero.

En conclusión, dado que a lo largo de trayectorias rectilíneas el límite es 0, mientras que sobre algunas trayectorias curvas se obtienen valores diferentes, se deduce que el límite global de la función no existe cuando \((x,y) \to (0,0)\).