Primera Identidad Fundamental de la Trigonometría
La primera identidad fundamental de la trigonometría establece que la suma del cuadrado del seno y del cuadrado del coseno de un ángulo es siempre igual a 1: $$ \sin^2 \alpha + \cos^2 \alpha = 1 $$
Esta identidad resulta sumamente útil, ya que permite calcular el valor del seno si conocemos el del coseno, y viceversa:
$$ \sin \alpha = \pm \sqrt{1 - \cos^2 \alpha } $$
$$ \cos \alpha = \pm \sqrt{1 - \sin^2 \alpha } $$
Demostración de la Identidad
La demostración de esta identidad se basa directamente en el Teorema de Pitágoras.
En la circunferencia unitaria, el seno, el coseno y el radio forman un triángulo rectángulo.
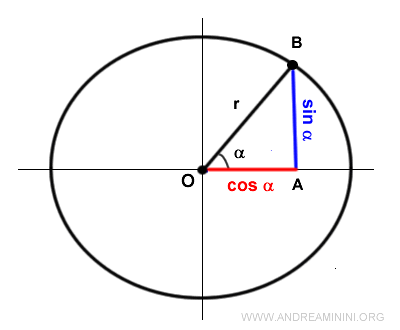
En dicho triángulo, el seno y el coseno representan las longitudes de los catetos, mientras que el radio corresponde a la hipotenusa.
Según el Teorema de Pitágoras, la longitud de la hipotenusa se obtiene como la raíz cuadrada de la suma de los cuadrados de los catetos:
$$ r = \sqrt{ \cos^2 \alpha + \sin^2 \alpha } $$
Elevando ambos miembros al cuadrado, obtenemos:
$$ r^2 = \left(\sqrt{ \cos^2 \alpha + \sin^2 \alpha }\right)^2 $$
$$ r^2 = \cos^2 \alpha + \sin^2 \alpha $$
Dado que el radio de la circunferencia unitaria es 1 (r = 1):
$$ 1^2 = \cos^2 \alpha + \sin^2 \alpha $$
Y puesto que 1 al cuadrado sigue siendo 1, se concluye que:
$$ 1 = \cos^2 \alpha + \sin^2 \alpha $$
Así queda demostrada la primera identidad fundamental de la trigonometría:
$$ \cos^2 \alpha + \sin^2 \alpha = 1 $$
A partir de esta identidad, también podemos deducir las fórmulas que expresan el seno en función del coseno y viceversa.
Para despejar el seno:
$$ \sin^2 \alpha = 1 - \cos^2 \alpha $$
Tomamos la raíz cuadrada en ambos lados:
$$ \sqrt{ \sin^2 \alpha } = \sqrt{ 1 - \cos^2 \alpha } $$
Y simplificamos:
$$ \sin \alpha = \sqrt{ 1 - \cos^2 \alpha } $$
Así obtenemos la fórmula que permite calcular el seno a partir del coseno.
Nota: De forma análoga, podemos deducir la fórmula para el coseno a partir de la identidad fundamental: $$ \cos^2 \alpha + \sin^2 \alpha = 1 $$ Despejando el coseno: $$ \cos^2 \alpha = 1 - \sin^2 \alpha $$ Tomamos la raíz cuadrada en ambos lados: $$ \sqrt{ \cos^2 \alpha } = \sqrt{ 1 - \sin^2 \alpha } $$ Y simplificamos: $$ \cos \alpha = \sqrt{ 1 - \sin^2 \alpha } $$
Con esto concluye la demostración.
Y así sucesivamente.