Cotangente
En la circunferencia unitaria, la cotangente de un ángulo alfa se define como el recíproco de la tangente, es decir, el cociente entre el coseno y el seno de dicho ángulo: $$ \cot \ \alpha = \frac{1}{\tan \alpha} = \frac{\cos \alpha}{\sin \alpha} $$ Se representa mediante los símbolos cot, ctg o cotg.
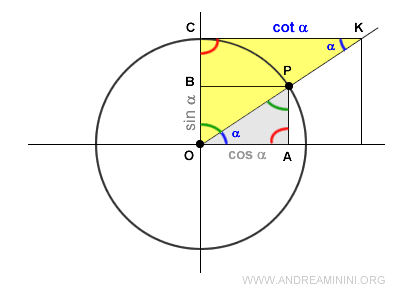
Desde un punto de vista geométrico, la cotangente se corresponde con el segmento CK.
Dicho segmento se obtiene prolongando el radio OP hasta que corta en el punto K una recta paralela al eje x, tangente a la circunferencia unitaria en CK.
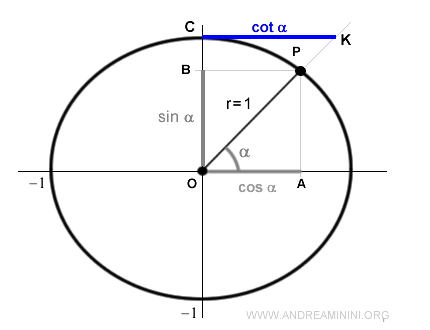
Por definición, la cotangente es el cociente entre la coordenada x (OA) y la coordenada y (OB) del punto P.
A partir de esta definición se deducen otras fórmulas:
$$ cotg \ \alpha = \frac{\overline{OA}}{\overline{OB}} = \frac{\cos \alpha}{\sin \alpha} = \frac{1}{\tan \alpha} $$
Aquí, el segmento OA representa el coseno y el segmento OB representa el seno del ángulo α que determina el punto P.
Nota. La cotangente no está definida en aquellos ángulos donde la coordenada y (el seno) es cero. En estos casos se produce una división por cero, lo que la hace indefinida. Por tanto, la cotangente no existe en los ángulos donde el seno se anula.
El término «cotangente» fue introducido por el matemático inglés Edmund Gunter en el siglo XVII.
Propiedades de la función cotangente
La cotangente es una función periódica cuyo periodo es π (o 180°):
$$ cotg \ \alpha = \cot( \alpha + n \cdot \pi ) $$
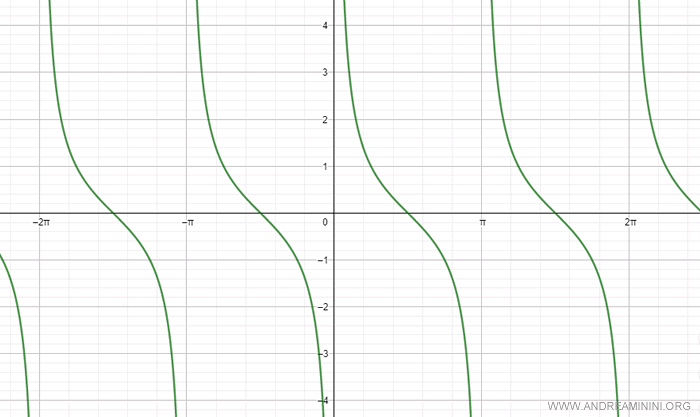
A continuación se muestra la gráfica de la cotangente en el intervalo de -2π a 2π.
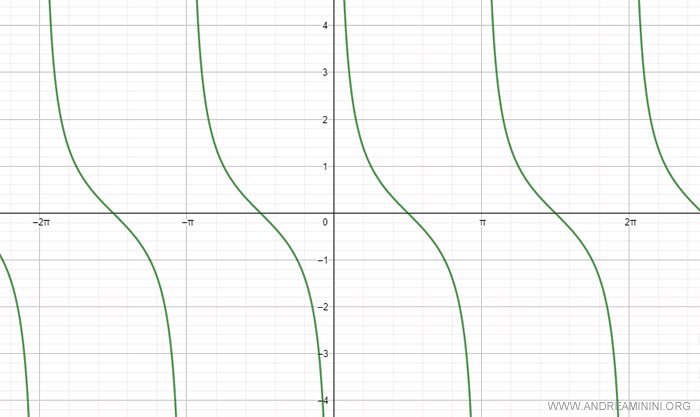
Nota. Dado que la cotangente tiene periodo π, suele estudiarse en el intervalo (0, π). En este intervalo, es una función continua, monótona y decreciente.
La cotangente no está definida en los ángulos 0 y en los múltiplos k·π, donde k es un número entero, pues en esos puntos el seno se anula (sen 0 = 0).
$$ \alpha = k \cdot \pi $$
El gráfico de la cotangente presenta asíntotas verticales en los ángulos α = k·π, donde la función no está definida.
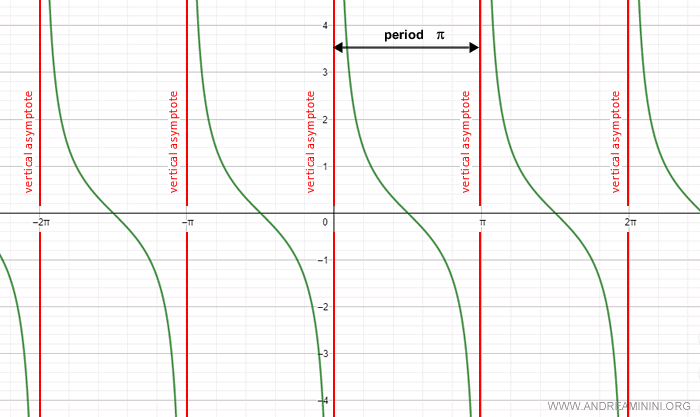
El dominio de la función cotangente comprende todos los números reales, salvo los múltiplos enteros de π:
$$ cotg \ \alpha : \ R \setminus \{ k \cdot \pi \} \ \rightarrow R \quad \text{con} \ k \in \mathbb{Z} $$
El recorrido es el conjunto de todos los números reales.
Por tanto, los valores de la cotangente oscilan entre -∞ y +∞.
Ángulos notables de la cotangente
La siguiente tabla recoge los valores de la cotangente para ángulos notables:
| Grados | Radianes | Cotangente |
|---|---|---|
| 0° | 0 | indefinida |
| 15° | π/12 | 2 + √3 |
| 30° | π/6 | √3 |
| 45° | π/4 | 1 |
| 60° | π/3 | (√3)/3 |
| 75° | 5π/12 | 2 - √3 |
| 90° | π/2 | 0 |
| 180° | π | indefinida |
| 270° | 3π/2 | 0 |
| 360° | 2π | indefinida |
Demostración
Consideremos un ángulo α que determina un punto P sobre la circunferencia unitaria.
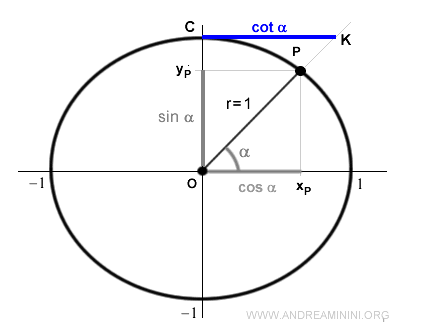
La cotangente es la función que asocia al ángulo α el cociente entre la coordenada xP y la coordenada yP del punto P:
$$ cotg \ \alpha = \frac{x_P}{y_P} $$
En la circunferencia unitaria, la coordenada xP corresponde al coseno y la coordenada yP al seno.
$$ cotg \ \alpha = \frac{x_P}{y_P} = \frac{\cos \alpha}{\sin \alpha} $$
Dado que la tangente se define como el cociente entre el seno y el coseno, tan = sen/cos, su recíproco es 1/tan = cos/sen.
Por tanto, la cotangente también puede expresarse como el recíproco de la tangente:
$$ cotg \ \alpha = \frac{x_P}{y_P} = \frac{\cos \alpha}{\sin \alpha} = \frac{1}{\tan \alpha} $$
Nota. La igualdad entre la cotangente y el recíproco de la tangente solo es válida cuando el ángulo alfa no es múltiplo de π ni de π/2: $$ cotg \ \alpha = \frac{1}{\tan \alpha} \quad , \quad \text{con} \ \alpha \ne k \cdot \frac{\pi}{2} $$ ya que en los múltiplos de π la cotangente no está definida y en los múltiplos de π/2 la tangente tampoco lo está. Por tanto, esta igualdad solo se cumple en un subconjunto del dominio de la cotangente.
Demostración geométrica
Consideremos un ángulo orientado cualquiera, distinto de π y π/2.
En la circunferencia unitaria, los triángulos formados son semejantes porque comparten los mismos ángulos.
Por semejanza, se establece la siguiente proporción entre los lados correspondientes:
$$ \overline{CK} : \overline{OA} = \overline{OC} : \overline{AP} $$
o, de forma equivalente:
$$ \frac{ \overline{CK} }{ \overline{OA} } = \frac{ \overline{OC} }{ \overline{AP} } $$
Sabiendo que el segmento CK representa la cotangente del ángulo α:
$$ \frac{ cotg \ \alpha }{ \overline{OA} } = \frac{ \overline{OC} }{ \overline{AP} } $$
El segmento OC es igual al radio de la circunferencia unitaria, es decir, r = 1.
$$ \frac{ cotg \ \alpha }{ \cos \alpha } = \frac{ 1 }{ \sin \alpha } $$
Despejando la cotangente, se obtiene la fórmula que se quería demostrar:
$$ cotg \ \alpha = \frac{ \cos \alpha }{ \sin \alpha } $$
La función inversa de la cotangente
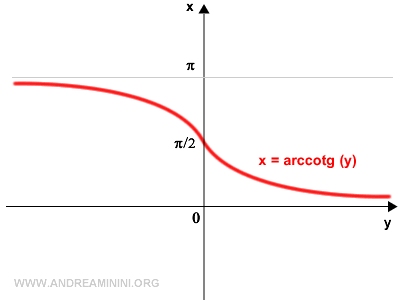
La función inversa de la cotangente se denomina arcocotangente.
La cotangente no es invertible en todo su dominio, debido a su carácter periódico.
No obstante, al restringir su dominio al intervalo (0, π), la cotangente se convierte en una función biyectiva.
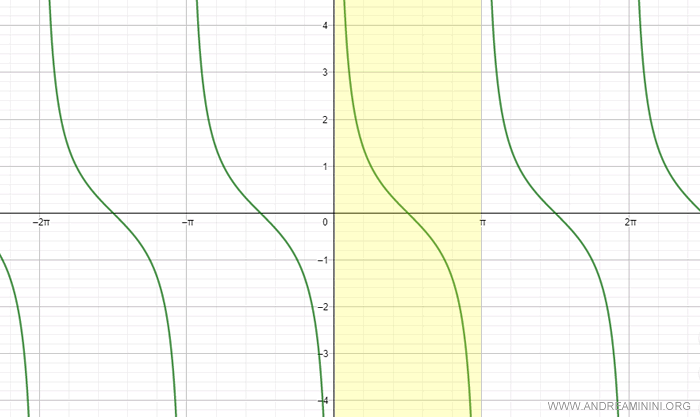
Nota. Existen infinitos intervalos en los que la cotangente es biyectiva, como (-π, 0) o (π, 2π). Aunque habitualmente se utiliza el intervalo (0, π), se pueden elegir otros intervalos según la necesidad.
En el intervalo (0, π), la cotangente es perfectamente invertible.
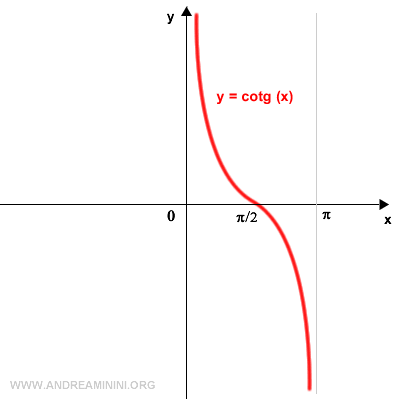
Para obtener el gráfico de la función inversa, se rota la gráfica 90° en sentido antihorario.
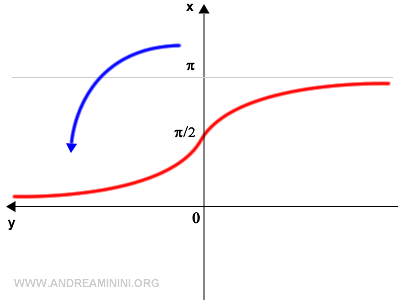
Posteriormente, se refleja horizontalmente respecto al eje y.
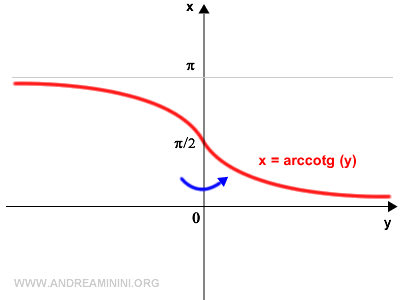
Así se obtiene la gráfica de la función inversa de la cotangente, conocida como arcocotangente.
Y así sucesivamente.
