Funciones Impares

¿Qué son las funciones impares?

Una función se considera impar si, para todo x perteneciente a su dominio, se cumple la siguiente condición: $$ f(-x) = -f(x) \quad \forall \ x \in D $$

El gráfico de una función impar presenta simetría respecto al origen. Esto significa que, para cada punto P(x, y), existe un punto simétrico P(-x, -y).

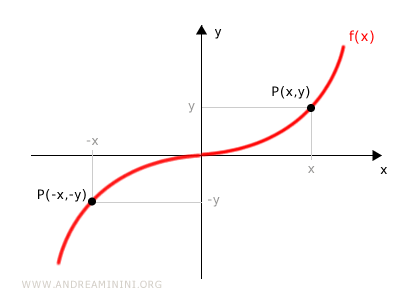
¿Cómo identificar si una función es impar?

Existen dos métodos principales para comprobarlo:

• Desde un enfoque analítico, se compara el valor de f(-x) con -f(x). Si ambos coinciden, la función es impar. $$ f(-x) = -f(x) $$

  Ejemplo. Consideremos la función f(x) = x³. Sustituyamos x por -x y comprobemos si el resultado coincide con -f(x): $$ f(-x) = (-x)^3 = -x^3 = -f(x) $$ Dado que f(-x) coincide con -f(x), la función es impar.

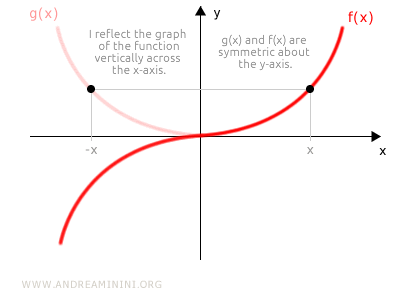
• Desde el punto de vista gráfico, se refleja la gráfica primero respecto al eje y y luego respecto al eje x. Si tras estas simetrías la gráfica resultante coincide con la original, la función es impar.
  

Nota. Que una función no sea par no implica necesariamente que sea impar, y viceversa. Por ejemplo, la función f(x) = x + x² no es impar: $$ f(-x) = (-x) + (-x)^2 = -x + x^2 \ne -f(x) = -x - x^2 $$ ni es par: $$ f(-x) = (-x) + (-x)^2 = -x + x^2 \ne f(x) = x + x^2 $$

Un ejemplo práctico

Un caso muy conocido de función impar es la función seno.

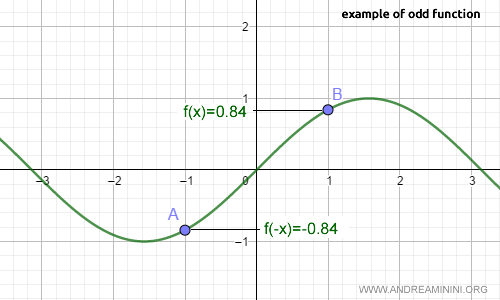
Para cualquier valor de x en el dominio de la función seno, se verifica que f(-x) = -f(x).

Nota. Por ejemplo, para x = 1, sen(1) ≈ 0,84. Si evaluamos la función en -1, obtenemos sen(-1) ≈ -0,84, lo que coincide exactamente con -sen(1). Por tanto, f(-x) = -f(x).

Ejemplo 2

Otra función impar es f(x) = x³.

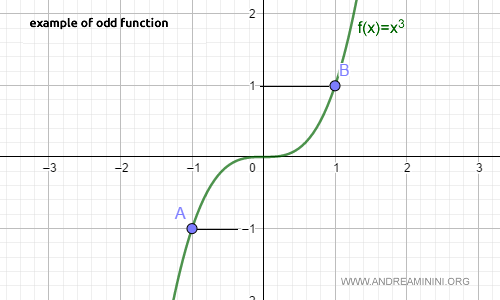
Para cualquier x perteneciente a su dominio, se cumple que f(-x) = -f(x).

Nota. En general, si una función está compuesta únicamente por potencias de x con exponentes impares, es una función impar.

Ejemplo 3

Analicemos si la siguiente función es impar:

$$ f(x) = x^2 + x $$

Sustituyamos x por -x en la expresión de la función:

$$ f(-x) = (-x)^2 + (-x) = x^2 - x $$

Este resultado no coincide con -f(x):

$$ -f(x) = -(x^2 + x) = -x^2 - x $$

Por tanto, esta función no es impar.

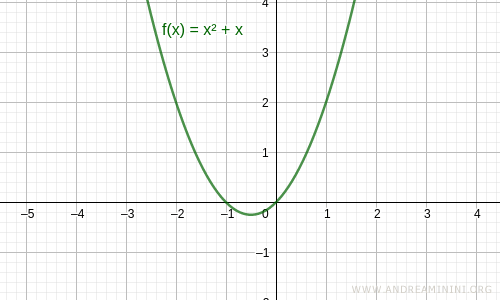
Nota. La función f(x) = x² + x tampoco es par, ya que no presenta simetría respecto al eje y.

Y así sucesivamente.