Función exponencial

La función exponencial es aquella que tiene la forma $$ y = a^x $$ donde la base $a$ es un número real positivo ($a > 0$). $$ a \in \mathbb{R}^+ $$

El dominio de la función exponencial es todo el conjunto de los números reales.

Su codominio es el conjunto de los números reales positivos.

$$ f:\mathbb{R} \;\to\; \mathbb{R}^+ $$

La forma de la gráfica de una función exponencial depende del valor de la base $a$:

• Si la base es mayor que uno ($a>1$), la gráfica crece de manera continua a medida que $x$ aumenta. En este caso, la función es biyectiva.
  
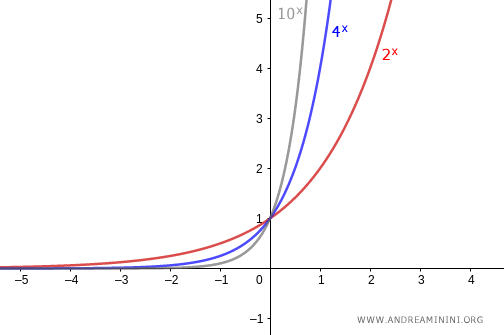
• Si la base es igual a uno ($a=1$), la gráfica es una recta constante en $y=1$. Se trata de una función no inyectiva.
  
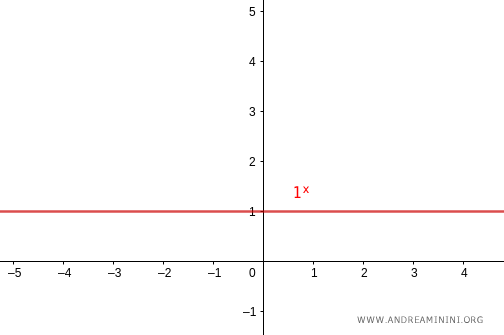
• Si la base está entre cero y uno ($0<a<1$), la gráfica decrece de forma monótona cuando $x$ aumenta. En este caso, la función también es biyectiva.
  

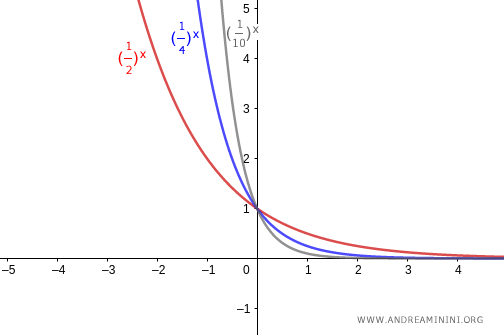
Nota. En todos los casos, la gráfica de una función exponencial pasa por el punto $(0,1)$ en el eje $y$ y nunca llega a cortar el eje $x$. La función siempre toma valores positivos y resulta continua en todo el conjunto de los números reales.

Y así sucesivamente.