Ceros de una Función

Un número real $ x $ se denomina cero de una función $ y = f(x) $ cuando, al evaluarlo, la función toma el valor cero: $$ f(x) = 0 $$

En términos gráficos, los ceros de una función corresponden a los puntos en los que su curva intersecta el eje x.

Ejemplo Ilustrativo

Consideremos la función:

$$ f(x) = x^2 - 4x $$

Para determinar sus ceros, buscamos los valores de $ x $ que anulan la función:

$$ f(x) = 0 $$

Esto equivale a resolver la ecuación:

$$ x^2 - 4x = 0 $$

Se trata de una ecuación cuadrática que puede resolverse fácilmente extrayendo el factor común $ x $:

$$ x(x - 4) = 0 $$

La igualdad se cumple cuando $ x = 0 $ o $ x = 4 $.

Por lo tanto, los ceros de la función son $ x_1 = 0 $ y $ x_2 = 4 $.

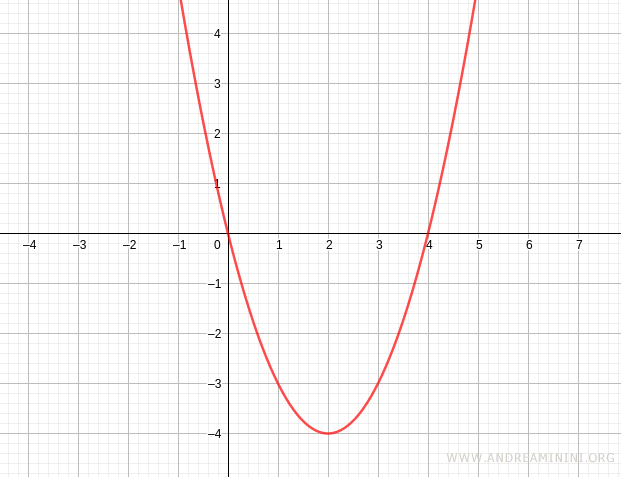
gráfica de la función con ceros en x igual a 0 y x igual a 4

En los puntos $ x_1 = 0 $ y $ x_2 = 4 $, la gráfica de la función corta el eje x, ya que en ambos casos el valor de la función es cero.

Y así sucesivamente.