Dominio de una Función

El dominio de una función o relación es el conjunto A en la aplicación $$ f:A \rightarrow B $$

El dominio representa el conjunto del cual la función toma sus valores de entrada.

El conjunto B es el conjunto de llegada y se denomina codominio de la función.

Diferencia entre dominio y dominio de definición

Los elementos de A (el dominio) que realmente se asocian con al menos un elemento de B (el codominio) constituyen un subconjunto denominado dominio de definición (o conjunto de existencia) de la función f.

En general, el dominio no coincide con el dominio de definición:

$$ f: D(f) \subseteq A \rightarrow B $$

El dominio es el espacio de referencia, mientras que el dominio de definición corresponde a la parte en la que la función está efectivamente definida.

Nota. En algunos textos, el término “dominio” se emplea con un significado distinto: se entiende como el conjunto de elementos de A que se relacionan con al menos un elemento de B mediante la relación R. En ese caso, el dominio coincide con el dominio de definición.

Ejemplo Práctico

Consideremos dos conjuntos finitos X e Y:

$$ X = \{1,2,3,4,5 \} $$

$$ Y = \{1,2,3,4,5,6,7,8,9 \} $$

y la relación/función:

$$ f: y = x^2 $$

El dominio de esta relación es todo el conjunto X:

$$ \text{Dom}(f) = \{1,2,3,4,5 \} $$

El dominio de definición es un subconjunto del dominio:

$$ D_f = \{1,2,3 \} \subseteq X $$

Son precisamente los elementos de X cuyos cuadrados pertenecen al codominio Y.

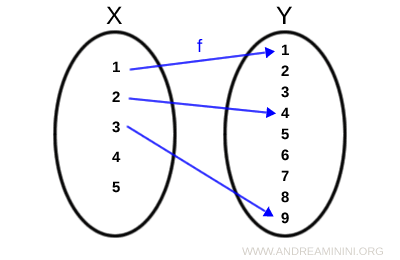
$$ f: 1^2 \mapsto 1 $$

$$ f: 2^2 \mapsto 4 $$

$$ f: 3^2 \mapsto 9 $$

Ejemplo 2

Consideremos la función real:

$$ f: y = \sin(x) $$

En este caso, tanto el dominio como el codominio son el conjunto de los números reales:

$$ f: \mathbb{R} \rightarrow \mathbb{R} $$

Aquí el dominio de definición coincide con el dominio, ya que la función seno está definida para todos los números reales.