Funciones de dos variables
¿Qué es una función de dos variables?
Una función de dos variables asigna a cada par de valores (x, y) de su dominio un valor único z en el codominio. $$ z=f(x,y) $$
En el caso de funciones reales, el dominio (o conjunto de definición) está constituido por pares de números reales.
$$ \mathbb{R}^2 = \{(x,y) : x,y \in \mathbb{R}\} $$
El codominio, por su parte, es un conjunto de números reales.
$$ f: \: \mathbb{R}^2 \rightarrow \mathbb{R} $$
Nota: Aquí x e y son las variables independientes, mientras que z es la variable dependiente. Sin embargo, la elección de las letras es arbitraria. $$ f: \: (x,y) \mapsto z $$
Formas de representar una función de dos variables
Representación en el espacio tridimensional
Para representar gráficamente una función de dos variables se utiliza un sistema de coordenadas cartesianas con tres ejes: x, y y z.
Así se obtiene una figura en el espacio tridimensional.

El plano (x, y) corresponde al producto cartesiano de los números reales, denotado como \(\mathbb{R}^2\) o \(\mathbb{R}\times \mathbb{R}\).
En consecuencia, el dominio de una función de dos variables es un subconjunto de dicho plano.

A cada par (x, y) del dominio le corresponde un valor en el eje z, dado por z = f(x, y).
De este modo, el codominio de una función de dos variables se representa como un punto en el espacio tridimensional.
Nota: Cada valor de la función se asocia a un punto del espacio tridimensional con coordenadas (x, y, z).
Representación en un plano
Una función z=f(x,y) también puede representarse en un plano bidimensional relacionando las variables de dos en dos, por ejemplo (x, z) y (y, z).
En este caso es necesario recurrir a dos gráficas independientes.
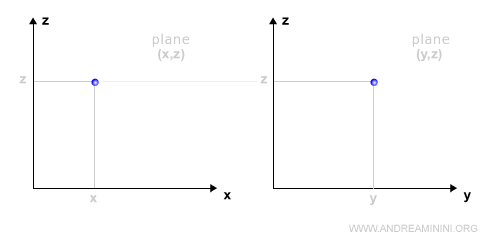
Este procedimiento resulta útil para analizar la relación de cada variable independiente con la variable dependiente.
Nota: La variable independiente que no aparece se proyecta ortogonalmente sobre el plano de las otras dos.
Cómo trazar la gráfica de una función de dos variables
El método más eficaz para representar una función de dos variables es el método punto por punto, el mismo que emplean los ordenadores para generar estas superficies.
- Se coloca una retícula de puntos en el plano Oxy, que corresponde a las variables independientes de f(x,y).
- Se calcula el valor de z = f(x,y) en cada punto de la retícula.
- Se conectan los puntos vecinos mediante líneas, formando una malla.
El resultado es una superficie tridimensional en el espacio.
Ejemplo
Consideremos la función:
$$ z= f(x,y) = \frac{3}{x+y+1} $$
En primer lugar se construye una retícula de puntos en el plano Oxy para las variables independientes.
Por ejemplo, tomemos la región del plano delimitada por los puntos (0,0) y (3,3).
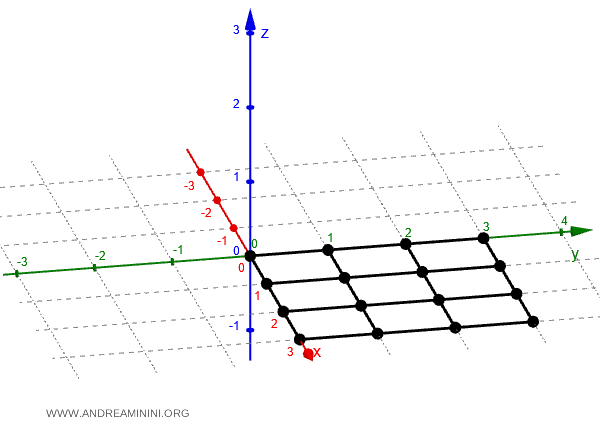
Después se calcula el valor de $ z $ en cada uno de esos puntos.
| x | y | z = 3 / (x + y + 1) |
|---|---|---|
| 0 | 0 | 3.0 |
| 0 | 1 | 1.5 |
| 0 | 2 | 1.0 |
| 0 | 3 | 0.75 |
| 1 | 0 | 1.5 |
| 1 | 1 | 1.0 |
| 1 | 2 | 0.75 |
| 1 | 3 | 0.6 |
| 2 | 0 | 1.0 |
| 2 | 1 | 0.75 |
| 2 | 2 | 0.6 |
| 2 | 3 | 0.5 |
| 3 | 0 | 0.75 |
| 3 | 1 | 0.6 |
| 3 | 2 | 0.5 |
| 3 | 3 | 0.4 |
En cada punto (x, y) se eleva un segmento vertical paralelo al eje $ z $, cuya altura corresponde al valor calculado. Finalmente, se unen los puntos adyacentes para formar una superficie continua.
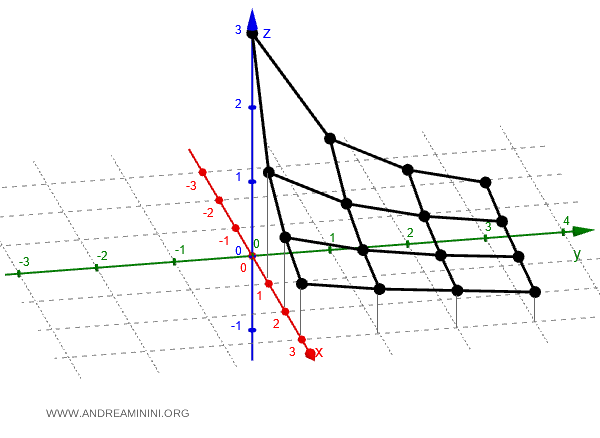
Este procedimiento da lugar a la superficie que representa la función $ f(x,y) $.
Otro ejemplo práctico
Veamos ahora otra función de dos variables:
$$ z= f(x,y) = x^2-y^2 $$
Su representación gráfica en coordenadas cartesianas tridimensionales es la siguiente:

Esta superficie se conoce como paraboloide hiperbólico.
Para representarla en un plano, fijemos primero la variable x en cero:
$$ z= f(0,y) = -y^2 $$
Luego fijemos la variable y en cero:
$$ z= f(x,0) = x^2 $$
De este modo se obtienen las proyecciones de la función sobre los planos (y, z) y (x, z).
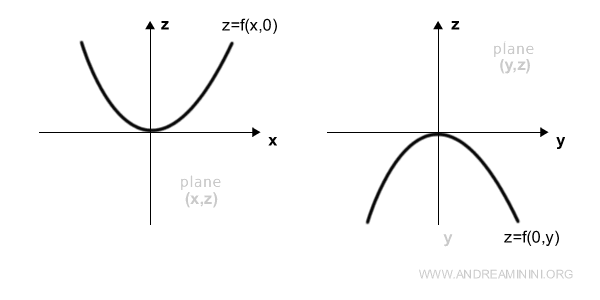
Y así sucesivamente.