Bola abierta (o entorno esférico)
Una bola abierta (también llamada entorno esférico abierto) es el conjunto de todos los puntos cuya distancia a un punto fijo \( x \) es menor que un radio dado \( r \): \[ B_r(x) = \{ y \in \mathbb{R}^n : \|y - x\| < r \} \] Aquí, \( x \) es el centro de la bola, \( r > 0 \) es el radio y \( \|y - x\| \) denota la distancia entre \( y \) y \( x \), normalmente la euclídea.
En matemáticas, la bola abierta es un concepto fundamental para precisar qué significa que un punto esté “próximo a” otro dentro de un espacio.
Se dice que una bola es "abierta" cuando no incluye la frontera, y "cerrada" cuando sí la incorpora.
Las bolas abiertas constituyen la base de nociones esenciales como la continuidad, la convergencia y la definición de conjuntos abiertos.
Ejemplos
Veamos algunos ejemplos concretos.
Ejemplo 1
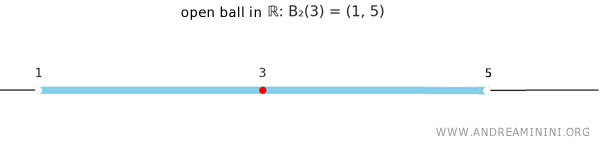
En la recta real \( \mathbb{R} \), las bolas abiertas se reducen a intervalos abiertos (o cerrados).
Por ejemplo, para el punto \( x = 3 \) y radio \( r = 2 \), la bola abierta es:
\[ B_2(3) = \{ y \in \mathbb{R} : |y - 3| < 2 \} = (1, 5) \]
Es simplemente un intervalo abierto centrado en 3 y de longitud total 4.
Ejemplo 2
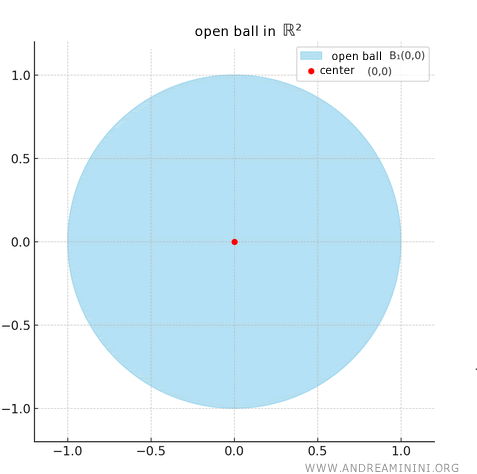
En el plano \( \mathbb{R}^2 \), una bola abierta corresponde a un disco abierto.
Por ejemplo, la bola abierta de centro en el origen y radio 1 es:
\[ B_1((0, 0)) = \{ (x, y) \in \mathbb{R}^2 : \sqrt{x^2 + y^2} < 1 \} \]
Al ser abierta, la circunferencia no forma parte del conjunto.
Ejemplo 3
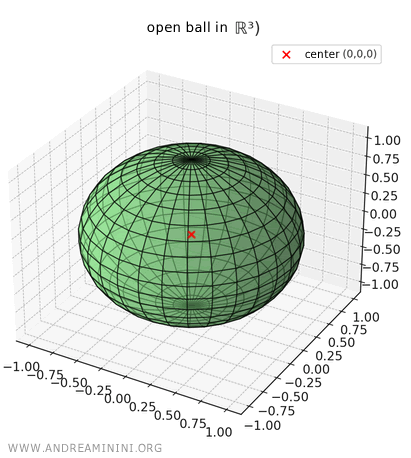
En el espacio tridimensional \( \mathbb{R}^3 \), una bola abierta es una esfera maciza sin su superficie:
\[ B_1((0, 0, 0)) = \{ (x, y, z) \in \mathbb{R}^3 : \sqrt{(x-0)^2 + (y-0)^2 + (z-0)^2} < 1 \} \]
Dicho de otro modo, es el interior de una esfera, excluida la capa exterior.
Al ser abierta, los puntos situados exactamente a distancia \( r = 1 \) quedan fuera del conjunto.
Bola cerrada (o entorno esférico cerrado)
Una bola cerrada sí incluye la frontera: contiene todos los puntos cuya distancia al centro es menor o igual que \( r \):
\[ \overline{B}_r(x) = \{ y \in \mathbb{R}^n : \|y - x\| \le r \} \]
En otras palabras, una bola cerrada es la bola abierta más la superficie de la esfera.
Ejemplo
Una bola cerrada en el plano, centrada en el origen y de radio 1, forma un círculo relleno:
\[ \overline{B}_1((0, 0)) = \{ (x, y) \in \mathbb{R}^2 : \sqrt{x^2 + y^2} \le 1 \} \]
En este caso, la circunferencia sí está incluida en el conjunto.
Propiedades esenciales de una bola
Toda bola -abierta o cerrada- presenta estas características fundamentales:
- Centro
Está definida en torno a un punto fijo \( x \), que actúa como referencia. - Simetría
Es simétrica, pues solo cuenta la distancia al centro; la dirección carece de importancia. - Importancia topológica
Son piezas básicas en topología, ya que proporcionan una definición rigurosa de “proximidad”.
Estas propiedades se mantienen en cualquier bola, abierta o cerrada, sin importar la dimensión del espacio.
¿Para qué sirven las bolas? Son herramientas indispensables para definir conceptos clave como la continuidad, los conjuntos abiertos, la convergencia o la estructura de una topología.
- Continuidad
Una función es continua en un punto \( x \) si, para todo entorno de \( f(x) \), existe un entorno de \( x \) que queda completamente contenido en él. - Conjuntos abiertos
Un conjunto es abierto si alrededor de cada uno de sus puntos existe una bola contenida íntegramente en el conjunto. - Convergencia
Una sucesión \( x_n \to x \) converge si, para cualquier bola centrada en \( x \), los términos de la sucesión acaban entrando y permaneciendo en ella. - Topologías
En los espacios métricos, las bolas abiertas constituyen la base de la topología.
Bolas en espacios no euclídeos
Desde el punto de vista matemático, las bolas (o entornos esféricos) pueden definirse en cualquier espacio métrico, no solo en el euclídeo.
Si la distancia se mide con una norma distinta de la euclídea, la forma de la bola cambia. No obstante, la idea central permanece: el conjunto de todos los puntos “cercanos” al centro dentro de un radio dado.
En general, en un espacio métrico, una bola abierta se define como:
\[ B_r(x) = \{ y \in X : d(x, y) < r \} \]
Aquí, \( X \) es el espacio, \( d(x, y) \) es una función de distancia general (no necesariamente euclídea) y \( r > 0 \) el radio.
La forma de la bola depende de la métrica o de la norma empleada.
Por ejemplo, con la métrica euclídea la bola es un círculo; con la métrica Manhattan, un rombo; y así sucesivamente.
A] Distancia Manhattan
Con la métrica Manhattan (o del taxista), la bola se define por:
\[ \|x - y\|_1 = \sum_{i=1}^n |x_i - y_i| \]
En \( \mathbb{R}^2 \), esto produce una región en forma de rombo centrada en \( x \), con lados inclinados 45° respecto de los ejes.
Por ejemplo, si \( r = 1 \):
\[ B_1((0,0)) = \{ (x, y) \in \mathbb{R}^2 : |x| + |y| < 1 \} \]
B] Distancia máxima (Chebyshev)
Con la métrica del máximo, la bola se define como:
\[ \|x - y\|_\infty = \max_i |x_i - y_i| \]
En \( \mathbb{R}^2 \), el resultado es un cuadrado centrado en \( x \), con lados paralelos a los ejes coordenados.
Por ejemplo, si \( r = 1 \):
\[ B_1((0,0)) = \{ (x, y) \in \mathbb{R}^2 : \max(|x|, |y|) < 1 \} \]
C] Espacio con métrica discreta
En un espacio con métrica discreta, la bola se define de la siguiente manera:
\[ d(x, y) = \begin{cases} 0 & \text{si } x = y \\ 1 & \text{si } x \ne y \end{cases} \]
En este caso, una bola abierta de radio 1 contiene únicamente el punto central \( x \), ya que todos los demás puntos están exactamente a distancia 1.
En cambio, la bola cerrada incluye todos los puntos del espacio.
Ejemplo
Sea el conjunto finito \( X = \{a, b, c\} \), con la métrica discreta definida como:
\[ d(x, y) =
\begin{cases}
0 & \text{si } x = y \\
1 & \text{si } x \ne y
\end{cases}
\]
Una bola abierta de radio 1 centrada en \( a \) incluye solo los puntos a distancia estrictamente menor que 1 de \( a \).
Dado que \( d(a, y) < 1 \) solo cuando \( y = a \), se obtiene:
\[ B_1(a) = \{ a \} \]
La bola cerrada centrada en \( a \), en cambio, contiene todos los puntos a distancia menor o igual que 1; es decir, todo el conjunto:
\[ \overline{B}_1(a) = \{ y \in X : d(a, y) \le 1 \} = \{a, b, c\} = X \]
Así, en un espacio con métrica discreta, una bola abierta contiene únicamente su centro, mientras que una bola cerrada abarca todo el espacio.
Parece un caso extremo, pero resulta muy útil para subrayar la diferencia entre bolas abiertas y cerradas, especialmente en contextos no geométricos.
Y así sucesivamente.