Puntos Máximos y Mínimos en Funciones de Varias Variables

En el caso de funciones con dos o más variables, los extremos locales (máximos y mínimos) pueden encontrarse en tres tipos de puntos:

• Puntos estacionarios. Aquellos en los que las derivadas parciales primeras se anulan: \[ \frac{\partial f}{\partial x} = 0 \quad \text{y} \quad \frac{\partial f}{\partial y} = 0 \]. Estos suelen ser los principales candidatos a extremos.
• Puntos singulares. Lugares en los que la función o sus derivadas dejan de existir -como ocurre en discontinuidades, cúspides o esquinas-. Estos casos suelen complicar mucho el análisis, por lo que, siempre que sea posible, se intentan evitar.
• Puntos de frontera. Si el dominio está acotado (por ejemplo, dentro de un círculo o un cuadrado), es imprescindible examinar lo que sucede en el borde, ya que los extremos también pueden producirse allí.

Nota. El procedimiento para identificar mínimos y máximos locales es muy parecido al de las funciones de una sola variable. Para funciones de una variable, \( y = f(x) \), los extremos se dan en puntos estacionarios, en puntos singulares y en los extremos de un intervalo cerrado \([a,b]\). En funciones de dos variables, \( z = f(x,y) \), los extremos se localizan en puntos estacionarios, en puntos singulares y en la frontera del dominio, que suele consistir en curvas cerradas, como la circunferencia de un círculo.

De acuerdo con el teorema de Weierstrass, si una función de dos o más variables es continua en un conjunto compacto (es decir, un conjunto cerrado y acotado), necesariamente alcanza un máximo absoluto y un mínimo absoluto en dicho conjunto.

En otras palabras, dentro del dominio existen puntos en los que la función adopta sus valores mayor y menor.

Nota. El teorema de Weierstrass proporciona una condición suficiente, aunque no necesaria, para garantizar la existencia de extremos absolutos. Por tanto, incluso cuando la función no sea continua o no se cumplan todas las hipótesis, aún puede haber puntos en los que se alcancen un máximo o un mínimo absolutos.

Un Ejemplo Práctico

Consideremos la función definida sobre la región \( x^2 + y^2 \leq 1 \):

\[ f(x,y) = x^2 + y^2 \]

En otras palabras, buscamos los extremos de la función dentro de un círculo de radio 1 centrado en el origen.

Las derivadas parciales son:

$$ \frac{ \partial f }{ \partial x}   = 2x $$

$$ \frac{ \partial f }{ \partial y} = 2y $$

Al imponer que las derivadas parciales sean nulas, se obtiene el sistema:

$$ \begin{cases}  2x=0 \\ \\ 2y=0 \end{cases} $$

$$ \begin{cases}  x=0 \\ \\ y=0 \end{cases} $$

Así, existe un único punto estacionario en el origen \((0,0)\).

Este punto constituye claramente un mínimo local, ya que \( f(0,0) = 0 \), y la función solo puede tomar valores no negativos. En consecuencia, no es posible obtener valores inferiores a cero.

También debemos comprobar si existen puntos singulares y analizar la frontera.

En este caso, no aparecen puntos singulares dentro del dominio (el interior del círculo), pero sí debemos considerar lo que sucede en la frontera.

En la frontera, \(x^2 + y^2 = 1\). Dado que este es el valor máximo posible de \(f\) dentro del dominio, cada punto de la circunferencia corresponde a un máximo local.

Por tanto, la función alcanza un mínimo en el origen y una infinidad de máximos en la frontera.

Ejemplo 2

Busquemos ahora los extremos locales de la función:

\[ f(x,y) = xy \]

en el dominio:

\[ D = \{ (x,y) \, | \, x^2 + y^2 \leq 1 \} \]

De nuevo, el dominio es el círculo unitario, pero la función es más delicada, pues mezcla \(x\) y \(y\).

1] Puntos estacionarios

Primero identificamos los puntos estacionarios dentro del dominio.

Las derivadas parciales son:

\[ \frac{\partial f}{\partial x} = y \]

\[ \frac{\partial f}{\partial y} = x \]

Al igualarlas a cero se obtiene:

$$ \begin{cases}  x=0 \\ \\ y=0 \end{cases} $$

El único punto crítico vuelve a ser el origen, \((0,0)\).

Evaluando la función en este punto:

\[ f(0,0) = 0 \]

No obstante, a diferencia del ejemplo anterior, aquí no podemos afirmar directamente que se trate de un mínimo o un máximo, ya que \(f\) puede adoptar tanto valores positivos como negativos. Se requiere más análisis.

2] Puntos singulares

En este caso, no existen puntos singulares dentro del dominio.

3] La frontera

En la frontera tenemos:

\[ x^2 + y^2 = 1 \]

Podemos parametrizarla en coordenadas polares:

\[ x = \cos\theta, \quad y = \sin\theta \]

donde \(\theta\) varía de \(0\) a \(2\pi\).

Sustituyendo en \(f\), resulta:

\[ f(\cos\theta, \sin\theta) = \cos\theta \sin\theta \]

Mediante la identidad trigonométrica \(\sin(2\theta) = 2\sin\theta\cos\theta\), podemos reescribirla como:

\[ f(\theta) = \frac{1}{2} \sin(2\theta) \]

Ahora buscamos los valores extremos de \(f(\theta)\).

Como \(\sin(2\theta)\) oscila entre \(-1\) y \(1\), se deduce que \(\frac{1}{2} \sin(2\theta)\) varía entre \(-\frac{1}{2}\) y \(\frac{1}{2}\).

Por tanto, los extremos son:

• Máximo: \( f(\theta) = \frac{1}{2}\)
• Mínimo: \( f(\theta) = -\frac{1}{2}\)

Para localizar dónde ocurren, resolvemos cuándo \( \sin(2\theta) \) alcanza los valores \(1\) y \(-1\).

• \( \sin(2\theta) = 1 \) cuando \( 2\theta = \frac{\pi}{2} \), es decir, \( \theta = \frac{\pi}{4} \). El máximo se da en \(x = \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\), \(y = \sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\).
• \( \sin(2\theta) = -1 \) cuando \( 2\theta = \frac{3\pi}{2} \), es decir, \( \theta = \frac{3\pi}{4} \). El mínimo se da en \(x = \cos\left(\frac{3\pi}{4}\right) = -\frac{\sqrt{2}}{2}\), \(y = \sin\left(\frac{3\pi}{4}\right) = \frac{\sqrt{2}}{2}\).

En resumen, el máximo global se alcanza en \(\left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), con valor \(\frac{1}{2}\).

El mínimo global se alcanza en \(\left( -\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), con valor \(-\frac{1}{2}\).

Así pues, para esta función tanto el máximo como el mínimo global aparecen en la frontera del dominio, representada en el gráfico por la curva negra.

En cuanto al punto \((0,0)\), resulta ser un punto de silla: no corresponde ni a un máximo ni a un mínimo.

Ejemplo 3

Consideremos la función definida sobre el dominio \( A = [0,1] \times [0,2] \).

\[ f(x,y) = 2x + 3y \]

El conjunto \( A \) es cerrado y acotado, por tanto compacto. La función \( f \) es continua, al ser un polinomio de dos variables.

Por el teorema de Weierstrass, \( f \) debe alcanzar un máximo absoluto y un mínimo absoluto en \( A \).

En este caso, determinar los extremos es sencillo si razonamos de manera intuitiva.

Como \( f(x,y) \) es lineal, aumenta conforme crecen \( x \) o \( y \).

Por ello, el mínimo absoluto se da cuando \( x \) e \( y \) toman sus valores más pequeños en el dominio, es decir, \( x = 0 \) y \( y = 0 \).

\[ f(0,0) = 2 \cdot 0 + 3 \cdot 0 = 0 \]

En cambio, el máximo absoluto se alcanza cuando \( x \) e \( y \) adoptan los valores más grandes permitidos, esto es, \( x = 1 \) y \( y = 2 \).

\[ f(1,2) = 2 \cdot 1 + 3 \cdot 2 = 2 + 6 = 8 \]

Este ejemplo muestra que, con funciones sencillas como un polinomio de primer grado, es posible identificar los extremos absolutos sin necesidad de recurrir al cálculo de derivadas, simplemente observando cómo se comporta la función en todo el dominio.

Método de las Curvas de Nivel

El método de las curvas de nivel es un enfoque gráfico para localizar el máximo o el mínimo de una función \( f(x, y) \) sobre un conjunto \( A \) (el dominio de la función).

Se trata de una técnica intuitiva y visual, especialmente eficaz con funciones sencillas y dominios poligonales.

Cómo se aplica

El procedimiento, paso a paso, es el siguiente:

1. Representa el conjunto \( A \) en el plano \( (x,y) \).
2. Dibuja las curvas de nivel de \( f(x, y) \), es decir, las curvas a lo largo de las cuales la función permanece constante:  \[ f(x, y) = \lambda \]
3. Para hallar el máximo, identifica la curva de nivel más alta (la de mayor \( \lambda \)) que corta o roza \( A \). Del mismo modo, el mínimo corresponde a la curva de nivel más baja que aún intersecta \( A \).

Ejemplo

Tomemos \( f(x, y) = 2x - y \) y \( A \) como el triángulo con vértices en \( (0,0) \), \( (0,1) \) y \( (3,2) \).

Primero, esboza el dominio \( A \) en el plano; en este caso, forma un triángulo.

Para determinar el máximo y el mínimo de \( f(x, y) \) sobre \( A \), construimos las curvas de nivel de la función:

\[ f(x, y) = \lambda \]

\[ 2x - y = \lambda \]

\[ y = 2x - \lambda \]

Aquí, las curvas de nivel son rectas paralelas con pendiente descendente 2. A medida que \( \lambda \) aumenta, las rectas se desplazan hacia la derecha.

La curva de nivel más alta que todavía toca \( A \) pasa por el punto \( (3,2) \).

En ese punto, la función alcanza su valor máximo sobre \( A \):

\[ f(3, 2) = 2x - y = 2 \cdot 3 - 2 = 6 - 2 = 4 \]

Para encontrar el mínimo, seguimos la misma lógica e identificamos la curva de nivel más baja que aún intersecta el dominio.

Esa curva de nivel toca \( A \) en el punto \( (0,1) \).

En dicho punto, la función toma su valor mínimo sobre \( A \):

\[ f(0, 1) = 2x - y = 2 \cdot 0 - 1 = -1 \]

Así, con solo analizar las curvas de nivel y el dominio, determinamos los valores máximo y mínimo de la función.

Método de Parametrización

El método de parametrización es una técnica para estudiar una función y determinar sus extremos absolutos sobre un dominio acotado, en particular a lo largo de su frontera.

Resulta especialmente eficaz cuando se examina una función \( f(x, y) \) definida en una región cerrada y acotada.

Cómo funciona el método

La idea consiste en describir la frontera del dominio mediante parametrizaciones: transformaciones que expresan cada tramo de la frontera en función de un único parámetro \( t \).

1. Divide la frontera en segmentos simples (p. ej., rectas o curvas).
2. Parametriza cada segmento con una función \( \gamma(t) = (x(t), y(t)) \) que lo recorra.
3. Sustituye en la función original para obtener \( f(x(t), y(t)) \), ahora una función de una sola variable.
4. Halla los valores máximo y mínimo en cada segmento.
5. Repite el proceso para todos los tramos de la frontera.
6. Compara todos los valores obtenidos para identificar los máximos y mínimos globales en el dominio.

Este enfoque reduce un problema de optimización en dos variables a una colección de problemas en una sola variable.

Es especialmente útil para dominios delimitados por curvas o aristas rectas, como rectángulos, círculos y polígonos.

Por ejemplo, si uno de los lados de la frontera es el segmento que va de \((x,y)= (2,1) \) a \( (x,y)=(5,1) \), una parametrización adecuada es:  \[  x(t) = t,\quad y(t) = 1,\quad \text{con } t \in [2,5] \] La función \( f(x,y) \) se reexpresa entonces como función de una sola variable: \[ f(x(t), y(t)) = f(t, 1) \]

Ejemplo

Considera la función

$$ f(x,y) = x^2 + y^2 $$

en el dominio rectangular

$$ A = [1,5] \times [-1,2] $$

Queremos identificar los puntos donde la función alcanza sus valores mínimo y máximo sobre este dominio.

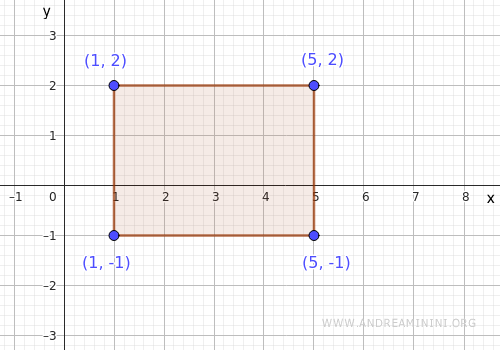
Analizamos tres aspectos: puntos estacionarios interiores, puntos singulares interiores y comportamiento en la frontera.

1] Puntos estacionarios interiores

Primero, calcula el gradiente de la función:

\[ \nabla f(x,y) = (2x, 2y) \]

Después, resuelve dónde el gradiente se anula:

$$ \begin{cases} 2x=0 \\ \\ 2y = 0 \end{cases} $$

Esto ocurre en el punto \( (0,0) \):

\[ \nabla f(x,y) = (0,0) \Rightarrow x = 0,\ y = 0 \]

Sin embargo, \( (0,0) \) queda fuera del dominio \( [1,5] \times [-1,2] \); por tanto, no hay puntos críticos en el interior.

2] Puntos singulares interiores

A continuación, comprueba si la función deja de ser diferenciable en algún punto interior (es decir, donde no existan derivadas parciales).

En este caso, la función es diferenciable en todo el dominio, de modo que no hay singularidades interiores.

3] Análisis de la frontera

Para estudiar la función en la frontera, aplicamos el método de parametrización.

La frontera del rectángulo consta de cuatro lados. Examinamos cada uno por separado.

• Lado superior
  Es el segmento horizontal de \( (1,2) \) a \( (5,2) \). Lo parametrizamos como \( \gamma(t) = (t, 2) \), con \( t \in [1,5] \).
  
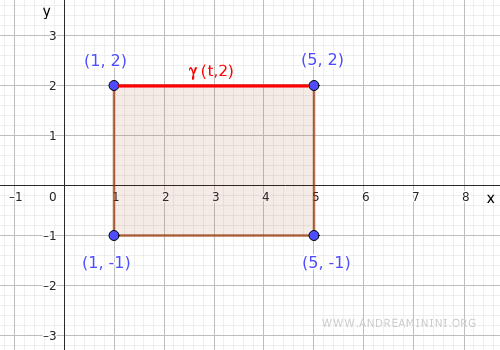
  Al sustituir en la función obtenemos: $$ f(t,2) = t^2 + 4 $$ Luego buscamos los extremos en el intervalo \( t \in [1,5] \)
  • Mínimo en \( t=1 \): \( f(1,2) = 1 + 4 = 5 \)
  • Máximo en \( t=5 \): \( f(5,2) = 25 + 4 = 29 \)
• Lado inferior
  Este segmento horizontal va de \( (1,-1) \) a \( (5,-1) \), parametrizado como \( \gamma(t) = (t, -1) \), con \( t \in [1,5] \).
  
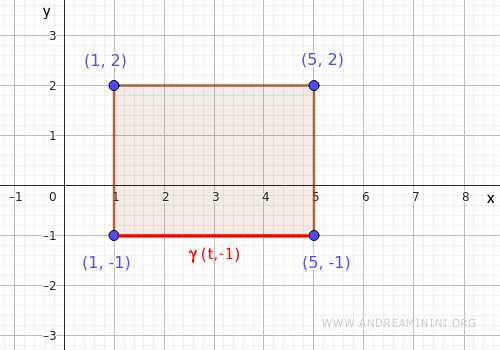
  Al sustituir en la función: $$ f(t,-1) = t^2 + 1 $$ Evaluamos en el intervalo \( t \in [1,5] \)
  • Mínimo: \( f(1,-1) = 1 + 1 = 2 \) 
  • Máximo: \( f(5,-1) = 25 + 1 = 26 \)
• Lado derecho
  Este segmento vertical va de \( (5,-1) \) a \( (5,2) \), y se parametriza como \( \gamma(t) = (5, t) \), con \( t \in [-1,2] \).
  
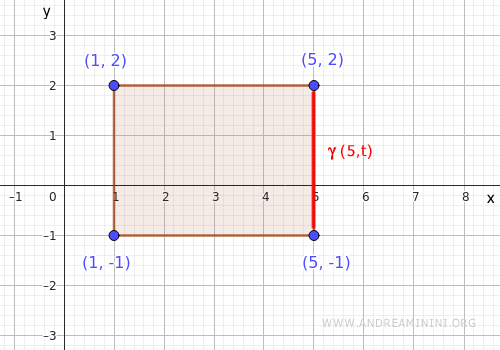
  Al sustituir en la función: $$ f(5,t) = 25 + t^2 $$ Analizamos para \( t \in [-1,2] \)
  • Mínimo en \( t=0 \): \( f(5,0) = 25 + 0 = 25 \) 
  • Máximo en \( t=2 \): \( f(5,2) = 25 + 4 = 29 \)
• Lado izquierdo
  Este segmento va de \( (1,-1) \) a \( (1,2) \), y lo parametrizamos como \( \gamma(t) = (1, t) \), con \( t \in [-1,2] \).
  
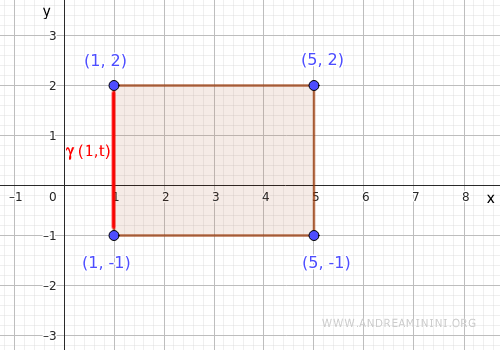
  Al sustituir en la función: $$ f(1,t) = 1 + t^2 $$ Después analizamos en \( t \in [-1,2] \)
  • Mínimo: \( f(1,0) = 1 + 0 = 1 \)
  • Máximo: \( f(1,2) = 1 + 4 = 5 \)

Si resumimos los resultados, obtenemos los siguientes puntos candidatos en la frontera para extremos globales:

\[
\begin{array}{|c|c|}
\hline
\textbf{Punto} & \textbf{f(x,y)} & \textbf{Clasificación} \\
\hline
(1,2) &  5  &\\
(5,2) &  29 & máximo \\
(5,0) & 25 & \\
(5,-1) & 26 & \\
(1,-1) &  2 & \\
(1,0) & 1 & mínimo \\
\hline
\end{array}
\]

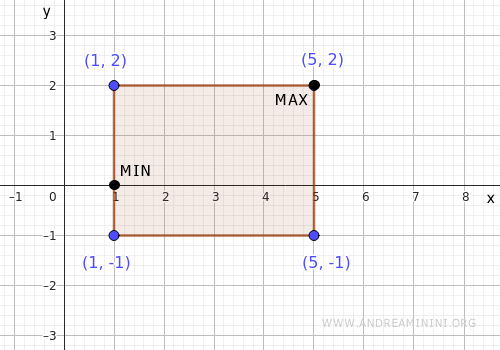
Por tanto, la función \( x^2+y^2 \) alcanza su mínimo absoluto en \( (1,0) \) y su máximo absoluto en \( (5,2) \). Los demás puntos pueden descartarse.

Método de los Multiplicadores de Lagrange

El método de los multiplicadores de Lagrange es una herramienta fundamental para localizar máximos y mínimos locales de una función cuando esta está sujeta a una restricción.

Es especialmente útil al optimizar una función $f(x, y)$ bajo una condición del tipo $g(x, y) = 0$.

El objetivo consiste en encontrar los puntos $(x, y)$ que maximizan o minimizan $f(x, y)$ respetando la restricción $g(x, y) = 0$.

La idea central es que, si $f(x, y)$ alcanza un extremo bajo la restricción, entonces en ese punto los gradientes de $f$ y $g$ deben ser paralelos:

$$ \nabla f(x, y) = \lambda \nabla g(x, y) $$

Donde:

• $\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right)$ es el gradiente de $f$
• $\nabla g = \left( \frac{\partial g}{\partial x}, \frac{\partial g}{\partial y} \right)$ es el gradiente de la restricción
• $\lambda$ es el multiplicador de Lagrange

Procedimiento

1. Plantear el sistema: $$
   \begin{cases}
   \frac{\partial f}{\partial x} = \lambda \frac{\partial g}{\partial x} \\
   \frac{\partial f}{\partial y} = \lambda \frac{\partial g}{\partial y} \\
   g(x, y) = 0
   \end{cases}
   $$
2. Resolverlo en las incógnitas $x$, $y$ y $\lambda$
3. Obtener los puntos críticos $(x, y)$
4. Evaluar $f(x, y)$ en cada punto para determinar si se trata de un máximo o de un mínimo

Nota. El método proporciona candidatos a extremos, pero no distingue de forma automática entre máximos y mínimos: cada caso debe analizarse por separado.

Ejemplo

Sea la función:

$$ f(x, y) = x^2 + y^2 $$

sujeta a la restricción:

$$ x + y = 1 $$

Reescribimos la restricción en la forma $g(x, y) = 0$:

$$ g(x, y) = x + y - 1 = 0 $$

Calculamos los gradientes:

$$ \nabla f = (2x, 2y) $$

$$ \nabla g = (1, 1) $$

Planteamos el sistema de Lagrange:

$$ \begin{cases}
2x = \lambda \\
2y = \lambda \\
x + y = 1
\end{cases} $$

De la primera y segunda ecuación se deduce $x = y$. Sustituyendo en la restricción:

$$ x = y, \quad 2x = 1 \quad \Rightarrow \quad x = \tfrac{1}{2},\ y = \tfrac{1}{2} $$

El punto crítico es $ \left( \tfrac{1}{2}, \tfrac{1}{2} \right) $.

Evaluamos la función:

$$ f \left( \tfrac{1}{2}, \tfrac{1}{2} \right) = \tfrac{1}{4} + \tfrac{1}{4} = \tfrac{1}{2} $$

Dado que $f(x, y) = x^2 + y^2$ crece con la distancia al origen y la restricción es una recta, este punto corresponde a un mínimo bajo la condición $x + y = 1$.

Método de los Puntos Estacionarios de la Restricción

El método de los puntos estacionarios de la restricción se basa en resolver el sistema: $$ \begin{cases} \Phi(x, y) = 0 \\ \frac{\partial \Phi}{\partial x}(x, y) = 0 \\ \frac{\partial \Phi}{\partial y}(x, y) = 0 \end{cases} $$ donde $\Phi(x, y)$ representa la restricción.

Se llaman puntos estacionarios de la restricción porque en ellos el gradiente de la restricción se anula.

Geométricamente, esto indica que la curva de restricción presenta una singularidad: cúspides, esquinas o zonas donde deja de ser suave.

Este método resulta especialmente útil cuando el gradiente de la restricción se anula, ya que en tales casos el método de Lagrange deja de ser aplicable.

Nota. El método de Lagrange presupone que el gradiente de la restricción es distinto de cero. Si se anula, las condiciones de regularidad fallan y el procedimiento no puede utilizarse.

Aun así, este enfoque no garantiza soluciones: el sistema puede no tener ninguna, o dar varias que habrá que estudiar individualmente.

En resumen, los puntos estacionarios de la restricción son candidatos a extremos condicionados, que deben evaluarse caso por caso.

Ejemplo

Consideremos la función:

$$ f(x,y) = x + y $$

con la restricción:

$$ \Phi(x, y) = (x - 1)^2 + y^2(y - 2)^2 $$

Calculamos las derivadas parciales:

$$ \frac{\partial \Phi}{\partial x} = 2(x - 1) $$

$$ \frac{\partial \Phi}{\partial y} = 2y(y - 2)^2 + 2y^2(y - 2) $$

El sistema queda:

$$ \begin{cases}
(x - 1)^2 + y^2(y - 2)^2 = 0 \\
2(x - 1) = 0 \\
2y(y - 2)^2 + 2y^2(y - 2) = 0
\end{cases} $$

De la segunda ecuación se obtiene $x = 1$. Sustituyendo en la primera:

$$ y^2(y - 2)^2 = 0 \quad \Rightarrow \quad y = 0 \ \text{o}\ y = 2 $$

Por tanto, los puntos candidatos son:

$$ (1, 0) \quad \text{y} \quad (1, 2) $$

Evaluando la función:

$$ f(1, 0) = 1, \quad f(1, 2) = 3 $$

Así, $ (1, 0) $ corresponde a un mínimo local y $ (1, 2) $ a un máximo local bajo la restricción.

En este caso concreto, la restricción $ \Phi(x, y) = 0 $ se reduce a dos puntos aislados: $ (1, 0) $ y $ (1, 2) $. Una vez identificado esto, el análisis completo resulta innecesario, pues basta con evaluar la función objetivo en dichos puntos.

Nota. Aquí el método de Lagrange no puede aplicarse porque el gradiente de la restricción se anula en ambos puntos: $\nabla \Phi = 0$. Recordemos: $$ \nabla \Phi(x, y) = \left( \frac{\partial \Phi}{\partial x}, \frac{\partial \Phi}{\partial y} \right) $$ En $ (1, 0) $: $$ \nabla \Phi = (0,0) $$ En $ (1, 2) $: $$ \nabla \Phi = (0,0) $$ Por tanto, no existe valor de $ \lambda $ que satisfaga la condición de Lagrange: $$ \nabla f = \lambda \nabla \Phi = \lambda (0,0) = (0,0) $$ Lo cual es imposible. De ahí que el método de Lagrange no pueda aplicarse en este ejemplo.

Matriz Hessiana

Para determinar los mínimos y máximos locales de una función de dos variables, como \( f(x, y) \), resulta especialmente útil la matriz hessiana.

La matriz hessiana es una matriz cuadrada que contiene todas las derivadas parciales de segundo orden de la función:\[
H = \begin{pmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
\end{pmatrix}
\]

En la diagonal principal figuran las derivadas parciales puras, \( \frac{\partial^2 f}{\partial x^2} \) y \( \frac{\partial^2 f}{\partial y^2} \), es decir, las que se obtienen al derivar dos veces con respecto a la misma variable.

En cambio, los elementos fuera de la diagonal corresponden a las derivadas parciales mixtas, \( \frac{\partial^2 f}{\partial x \partial y} \) y \( \frac{\partial^2 f}{\partial y \partial x} \), que implican derivar sucesivamente respecto de ambas variables.

Una vez construida la hessiana, se sustituyen en ella las coordenadas del punto crítico que se quiere analizar, reemplazando \(x\) e \(y\) por sus valores numéricos.

Nota. Si la hessiana está compuesta únicamente por constantes, puede aplicarse directamente en cualquier punto crítico, sin necesidad de sustituciones.

El siguiente paso consiste en calcular el determinante \( \Delta \) de la matriz:

• Si \( \Delta > 0 \) y \( \frac{\partial^2 f}{\partial x^2} > 0 \), el punto es un mínimo local.
• Si \( \Delta > 0 \) y \( \frac{\partial^2 f}{\partial x^2} < 0 \), el punto es un máximo local.
• Si \( \Delta < 0 \), se trata de un punto de silla: no corresponde ni a un máximo ni a un mínimo.
• Si \( \Delta = 0 \), el criterio es inconcluyente y es necesario un análisis adicional.

Ejemplo 1

En el ejercicio anterior estudiamos la función:

\[ f(x,y) = xy \]

definida sobre el dominio:

\[ D = \{ (x,y) \, | \, x^2 + y^2 \leq 1 \} \]

donde identificamos un punto crítico en \( P(0,0) \).

Para determinar la naturaleza de este punto, construimos la matriz hessiana:

\[ H = \begin{pmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} \\
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2}
\end{pmatrix} \]

Las derivadas parciales de primer orden son:

• \( \frac{\partial f}{\partial x} = y \)
• \( \frac{\partial f}{\partial y} = x \)

Las derivadas de segundo orden, necesarias para la hessiana, resultan ser:

• \( \frac{\partial^2 f}{\partial x^2} = 0 \)
• \( \frac{\partial^2 f}{\partial y^2} = 0 \)
• \( \frac{\partial^2 f}{\partial x \partial y} = 1 \)
• \( \frac{\partial^2 f}{\partial y \partial x} = 1 \)

Por tanto:

\[ H = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} \]

Como los elementos son constantes, la prueba se aplica directamente en \( P(0,0) \).

El determinante es:

\[ \Delta = (0)(0) - (1)(1) = -1 \]

Dado que es negativo (\(\Delta < 0\)), concluimos que \( P(0,0) \) es un punto de silla.

Este resultado coincide plenamente con lo que ya habíamos deducido por métodos directos.

Ejemplo 2

Consideremos ahora la función:

\[ f(x,y) = x^4 - 2xy + y^4 \]

definida en el dominio:

\[ D = \{ (x,y) \mid x^2 + y^2 \leq 4 \} \]

es decir, el disco de radio 2 centrado en el origen.

Las derivadas parciales de primer orden son:

• \( \frac{\partial f}{\partial x} = 4x^3 - 2y \)
• \( \frac{\partial f}{\partial y} = 4y^3 - 2x \)

Imponiendo que se anulen obtenemos:

\[ \begin{cases} 4x^3 - 2y = 0 \\ 4y^3 - 2x = 0 \end{cases} \]

De aquí se deduce \( y = 2x^3 \), que sustituido en la segunda ecuación conduce a:

\[ 32x^9 - 2x = 0 \quad \Rightarrow \quad 2x(16x^8 - 1) = 0 \]

Las soluciones son \( x = 0 \) o bien \( x = \pm \tfrac{1}{\sqrt{2}} \). Los valores correspondientes de \(y\) son:

• Si \(x = 0\), entonces \(y = 0\).
• Si \(x = \tfrac{1}{\sqrt{2}}\), entonces \(y = \tfrac{1}{\sqrt{2}}\).
• Si \(x = -\tfrac{1}{\sqrt{2}}\), entonces \(y = -\tfrac{1}{\sqrt{2}}\).

Los puntos críticos son:

• \((0,0)\)
• \(\left(\tfrac{1}{\sqrt{2}}, \tfrac{1}{\sqrt{2}}\right)\)
• \(\left(-\tfrac{1}{\sqrt{2}}, -\tfrac{1}{\sqrt{2}}\right)\)

Todos ellos pertenecen al disco de radio 2, ya que cumplen \(x^2 + y^2 \leq 4\).

Pasamos ahora a construir la matriz hessiana, a partir de las derivadas de segundo orden:

• \( \frac{\partial^2 f}{\partial x^2} = 12x^2 \)
• \( \frac{\partial^2 f}{\partial y^2} = 12y^2 \)
• \( \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} = -2 \)

De modo que:

\[ H = \begin{pmatrix} 12x^2 & -2 \\ -2 & 12y^2 \end{pmatrix} \]

1] En \((0,0)\):

\[ H(0,0) = \begin{pmatrix} 0 & -2 \\ -2 & 0 \end{pmatrix} \]

Determinante: \(\Delta = -4 < 0\). Conclusión: punto de silla.

2] En \(\left(\tfrac{1}{\sqrt{2}}, \tfrac{1}{\sqrt{2}}\right)\):

\[ H = \begin{pmatrix} 6 & -2 \\ -2 & 6 \end{pmatrix} \]

Determinante: \(\Delta = 36 - 4 = 32 > 0\). Como \( \frac{\partial^2 f}{\partial x^2} = 6 > 0 \), se trata de un mínimo local.

3] En \(\left(-\tfrac{1}{\sqrt{2}}, -\tfrac{1}{\sqrt{2}}\right)\):

Por simetría, el cálculo es idéntico:

\[ H = \begin{pmatrix} 6 & -2 \\ -2 & 6 \end{pmatrix}, \quad \Delta = 32 > 0 \]

También corresponde a un mínimo local.