Cómo determinar el mínimo y el máximo de una función de dos variables mediante curvas de nivel
El método de las curvas de nivel es una técnica gráfica que permite localizar el máximo o el mínimo de una función $f(x, y)$ sobre un conjunto $A$, es decir, dentro de su dominio.
Se trata de un procedimiento intuitivo y visual, especialmente útil para funciones sencillas y dominios acotados (por ejemplo, polígonos).
¿Qué son las curvas de nivel?
Son las curvas del plano $(x, y)$ en las que la función $f(x, y)$ se mantiene constante:
$f(x, y) = \lambda$
Dicho de otro modo, cada curva de nivel está formada por todos los puntos del plano donde la función adopta el mismo valor $\lambda$.
¿Cómo se aplica el método?
El procedimiento es directo y se apoya en una idea geométrica:
- Dibujar el dominio $A$
- Representar el conjunto $A$ en el plano $(x,y)$. Así se delimita la región en la que se buscarán el máximo y el mínimo de la función.
- Trazar las curvas de nivel de $f(x, y)$
- Dibujar varias curvas $f(x, y) = \lambda$ para distintos valores de $\lambda$. Cada una indica dónde la función vale $\lambda$.
- Identificar el máximo y el mínimo
El máximo corresponde a la curva de nivel más alta (es decir, al mayor $\lambda$) que corta o roza $A$.
El mínimo corresponde a la curva de nivel más baja (el menor $\lambda$) que toca $A$.
¿Cuándo resulta práctico este método? Funciona muy bien con funciones simples o simétricas (como las que involucran cuadrados, circunferencias o elipses) y con dominios poligonales o limitados. En definitiva, en situaciones en las que se puede visualizar con claridad el comportamiento de la función. Para funciones más complicadas o dominios irregulares, este método sigue ofreciendo una valiosa orientación cualitativa antes de recurrir a procedimientos analíticos más rigurosos.
Ejemplo
Consideremos la función:
$f(x, y) = x^2 + y^2$
y el dominio $A$, definido como el cuadrado $-1 \leq x \leq 1$, $-1 \leq y \leq 1$.
En primer lugar, representamos el cuadrado $A$ en el plano $(x, y)$.
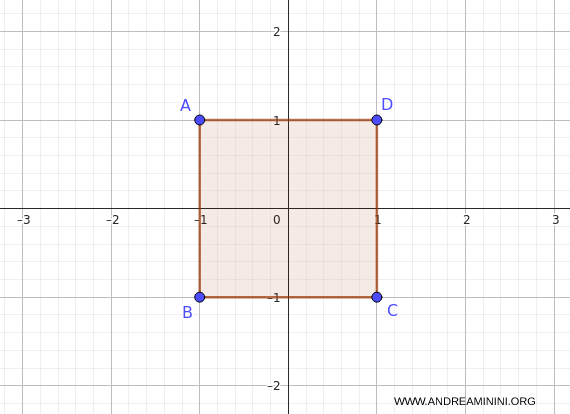
Las curvas de nivel de esta función son circunferencias de radio $\sqrt{\lambda}$ centradas en el origen.
$$ x^{2}+y^{2}=\lambda,\qquad \lambda\ge 0. $$
Si despejamos $y$, obtenemos:
$$ y^{2}=\lambda-x^{2}\quad\Longrightarrow\quad y=\pm\sqrt{\lambda-x^{2}} $$
Para que una curva de nivel corte el dominio $A$, el valor de $\lambda$ debe ser lo suficientemente grande como para que la circunferencia alcance o toque $A$.
A continuación, trazamos las curvas de nivel variando $ \lambda $.
Como $ \lambda \ge 0 $, solo se admiten valores no negativos.
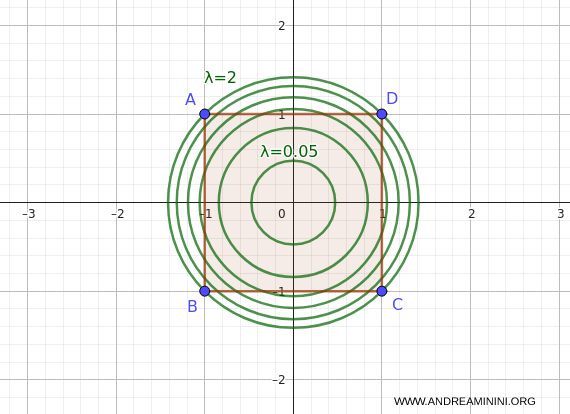
La curva de nivel más pequeña que corta $A$ es la circunferencia degenerada de radio 0, que corresponde al único punto $(0,0)$, donde $f(0,0) = 0$.
Por lo tanto, el mínimo absoluto de la función en este dominio es $0$, alcanzado en el punto $ (x,y)=(0,0) $.
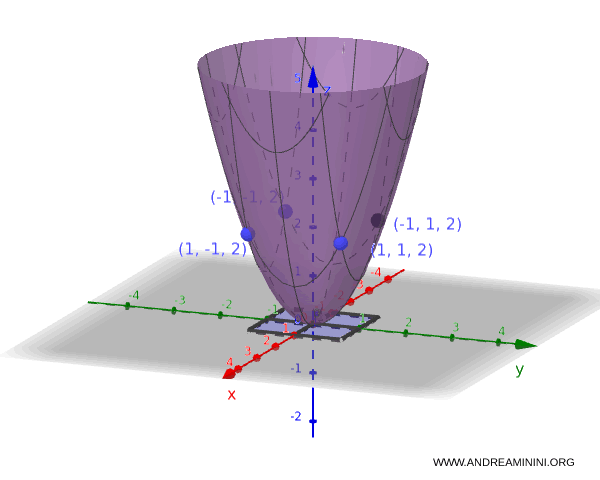
La curva de nivel más grande que todavía toca el dominio es la circunferencia que pasa por los vértices del cuadrado.
$$f(1,1) = 1^2 + 1^2 = 2$$
Así, el máximo absoluto de la función en el dominio es $2$, alcanzado en los puntos $(1,1)$, $(-1,1)$, $ (1,-1) $ y $ (-1,-1) $.
Con un simple esquema hemos localizado tanto el mínimo como el máximo de la función.
Ejemplo 2
Consideremos la función
$$ f(x,y) = x - 2y $$
sujeta a la restricción
$$ x^2 + y^2 \le 3 $$
Queremos determinar los valores máximo y mínimo de la función bajo esta restricción, aplicando el método de las curvas de nivel.
Comenzamos representando la restricción, que en este caso corresponde a la circunferencia $ x^2 + y^2 \le 3 $.
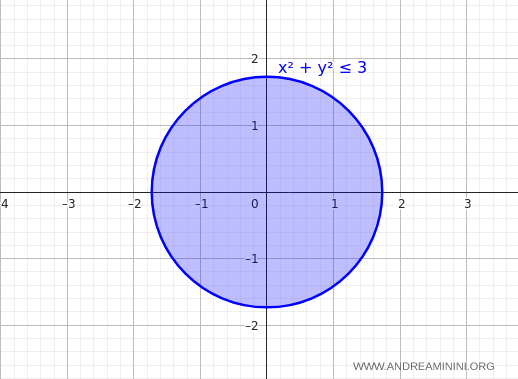
La función puede tomar distintos valores a lo largo del eje $z$, que denotamos con $ \lambda $:
$$ f(x,y) = x - 2y = \lambda $$
Podemos expresar $ y $ en función de $ x $ y $ \lambda $:
$$ x - \lambda = 2y $$
$$ y = \frac{x - \lambda}{2} $$
Ahora trazamos las curvas de nivel para diferentes valores de $ \lambda $.
Las curvas correspondientes a valores grandes de $ \lambda $ se sitúan más abajo en el plano, mientras que las asociadas a valores pequeños aparecen más arriba.
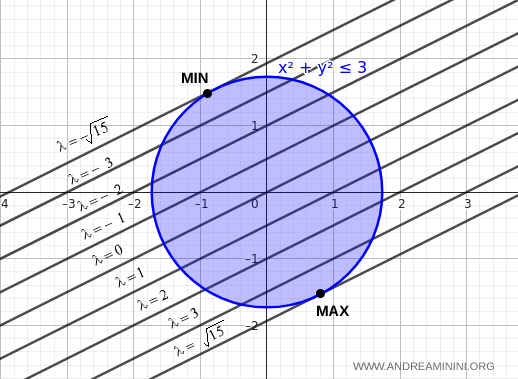
El valor máximo de $ f(x,y) $ se alcanza en el punto donde una curva de nivel es tangente al borde inferior de la circunferencia de restricción.
De modo análogo, el valor mínimo se obtiene cuando la curva de nivel es tangente al borde superior de la circunferencia.
¿Qué valores de $ \lambda $ corresponden al máximo y al mínimo?
La ecuación de las curvas de nivel es:
$$ y = \frac{x - \lambda}{2} $$
Si sustituimos en la ecuación de la circunferencia, resulta:
$$ x^2 + \left( \frac{x - \lambda}{2} \right)^2 = 3 $$
$$ x^2 + \frac{(x - \lambda)^2}{4} = 3 $$
Multiplicamos todo por 4 para eliminar denominadores:
$$ 4x^2 + (x - \lambda)^2 = 12 $$
Desarrollando el cuadrado:
$$ 4x^2 + x^2 - 2x\lambda + \lambda^2 = 12 $$
$$ 5x^2 - 2x\lambda + \lambda^2 = 12 $$
Obtenemos así una ecuación cuadrática en $ x $.
Para que la curva de nivel sea tangente a la circunferencia, la ecuación debe tener una única solución, es decir, el discriminante ha de anularse:
$$ \Delta = [-2\lambda]^2 - 4 \cdot 5 \cdot (\lambda^2 - 12) $$
$$ \Delta = 4\lambda^2 - 20(\lambda^2 - 12) $$
$$ \Delta = 4\lambda^2 - 20\lambda^2 + 240 $$
$$ \Delta = -16\lambda^2 + 240 $$
Si imponemos $ \Delta = 0 $:
$$ -16\lambda^2 + 240 = 0 $$
$$ 16\lambda^2 = 240 $$
$$ \lambda^2 = \frac{240}{16} $$
$$ \lambda^2 = 15 $$
$$ \lambda = \pm \sqrt{15} $$
En consecuencia, los valores máximo y mínimo de $ f(x,y) $ bajo la restricción son:
$$ \lambda_{max} = \sqrt{15} \approx 3.873 $$
$$ \lambda_{min} = -\sqrt{15} \approx -3.873 $$
Y así queda resuelto.