La derivada direccional

La derivada direccional de una función \( f \) en un punto \( (x_0, y_0) \), en la dirección del vector \( \vec{v} = (\alpha, \beta) \), se define como \[ \frac{\partial f}{\partial \vec{v}}(x_0,y_0) = \lim_{t \to 0} \frac{f(x_0 + t\alpha, \; y_0 + t\beta) - f(x_0, y_0)}{t} \]

En pocas palabras, damos un paso muy pequeño \( t \) en la dirección de \( \vec{v} \), observamos cuánto varía la función \( f \) y dividimos ese cambio entre la longitud del paso.

Este límite existe únicamente cuando el resultado es un número real y finito.

La derivada direccional amplía la idea de la derivada parcial, que mide la variación a lo largo de un eje de coordenadas.

De hecho, si escogemos \( \vec{v} = (1,0) \) o \( (0,1) \) -es decir, en la dirección del eje x o del eje y- la derivada direccional coincide exactamente con la derivada parcial correspondiente.

Nota. Una función de dos variables determina una superficie en el espacio tridimensional. Por ejemplo, si el gráfico se asemeja a una “colina” y el punto \( (x_0, y_0) \) se encuentra en su ladera, la derivada direccional nos indica con qué inclinación sube o baja la superficie en la dirección del vector \( \vec{v} \). Esa dirección no se restringe a los ejes x o y: puede ser diagonal o apuntar en cualquier sentido.

Geométricamente, la derivada direccional mide el ritmo de variación de la función a lo largo de la recta descrita por la ecuación paramétrica \( (x_0 + t\alpha, y_0 + t\beta) \).

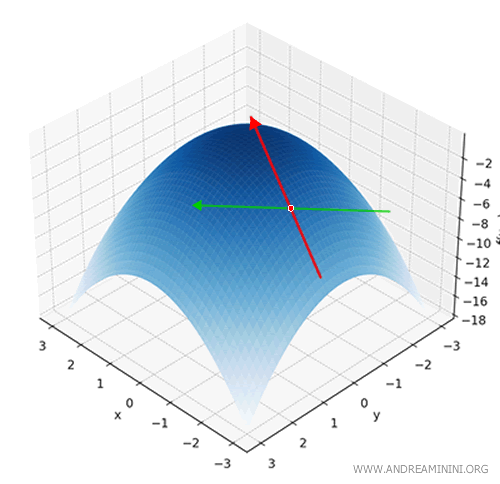
Dicho de otro modo, nos desplazamos a lo largo de una recta que parte de \( (x_0, y_0) \) y avanza en la dirección de \( \vec{v} = (\alpha, \beta) \):

\[ (x(t), y(t)) = (x_0 + t\alpha, \; y_0 + t\beta) \]

La derivada direccional nos indica la rapidez con que la función \( f \) crece o decrece al movernos en esa dirección.

Expresado de manera intuitiva: es la pendiente de la superficie si ascendemos en esa dirección -o la inclinación descendente, si avanzamos en sentido contrario.

Nota. Más en general, para una función \( f: \mathbb{R}^n \to \mathbb{R} \), donde \( \vec{x}_0 \in \mathbb{R}^n \) representa un punto del espacio y \( \vec{v} \in \mathbb{R}^n \) es un vector de dirección distinto de cero, la derivada direccional de \( f \) en \( \vec{x}_0 \) en la dirección de \( \vec{v} \) se expresa en notación vectorial como: \[ \frac{\partial f}{\partial \vec{v}}( \vec{x}_0 ) = \lim_{t \to 0} \frac{f(\vec{x}_0 + t \vec{v}) - f(\vec{x}_0)}{t} \] Aquí, \( \vec{x}_0 \) es un vector con coordenadas \( (x_1, x_2, ..., x_n) \), que representa un punto en \( \mathbb{R}^n \).

Un ejemplo concreto

Consideremos la función

\[ f(x, y) = x^2 + y^2 \]

Esta función describe un paraboloide -una superficie con forma de cuenco- y resulta sencilla de derivar.

Analicemos cómo varía la función \( f(x, y) = x^2 + y^2 \) al desplazarnos desde el punto \( (1, 2) \) en la dirección del vector \( \vec{v} = (3, 4) \).

Lo primero es normalizar el vector de dirección.

Para calcular correctamente la derivada direccional, dicho vector debe ser unitario, es decir, de longitud 1.

La norma de \( \vec{v} = (3, 4) \) es:

\[ \|\vec{v}\| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]

Por tanto, el vector unitario asociado es:

\[ \hat{v} = \left(\frac{3}{5}, \frac{4}{5} \right) \]

A continuación, calculamos el gradiente \( \nabla f(x, y) \), formado por las derivadas parciales:

\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) = (2x, 2y) \]

Evaluando en el punto \( (1, 2) \):

\[ \nabla f(1, 2) = (2 \cdot 1, 2 \cdot 2) = (2, 4) \]

Ahora calculamos el producto escalar entre el gradiente y el vector unitario \( \hat{v} \):

\[ \frac{\partial f}{\partial \vec{v}}(1, 2) = \nabla f(1, 2) \cdot \hat{v} = (2, 4) \cdot \left( \frac{3}{5}, \frac{4}{5} \right) \]

\[ = \frac{2 \cdot 3 + 4 \cdot 4}{5} = \frac{6 + 16}{5} = \frac{22}{5} \]

En consecuencia, la derivada direccional de \( f(x,y) = x^2 + y^2 \) en el punto \( (1,2) \), en la dirección \( \vec{v} = (3,4) \), es:

\[ \frac{\partial f}{\partial \vec{v}}(1,2) = \frac{22}{5} \]

Esto significa que, en el punto \( (1,2) \), si nos desplazamos en la dirección \( (3,4) \), la función crece a un ritmo de \( \frac{22}{5} \).

El teorema de la derivada direccional

Si la función \( f \) es diferenciable en un punto \( \vec{x}_0 \), entonces su derivada direccional en \( \vec{x}_0 \) en la dirección de un vector \( \vec{v} \) se obtiene como el producto escalar entre el gradiente de \( f \) en dicho punto y el vector de dirección \( \vec{v} \): \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \] Suele escribirse también de la forma \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \] donde el gradiente \( \vec{\alpha} = \nabla f(x_0) \) apunta hacia la dirección de máximo crecimiento de la función.

El producto escalar con \( \vec{v} \) mide cuánto de esa variación se proyecta en la dirección de \( \vec{v} \).

Si \( \vec{v} \) es ortogonal al gradiente, la derivada direccional es nula.

Si \( \vec{v} \) está alineado con el gradiente, la derivada direccional alcanza su valor máximo en esa dirección.

Ejemplo

Consideremos la función

\[ f(x,y) = x^2 + y^2 \]

Analicemos el punto \( \vec x_0 = (1,\,2) \) y el vector de dirección \( \vec v = (3,\,4) \).

En primer lugar, calculamos el gradiente de \(f(x,y)\):

\[ \nabla f(x,y) = \bigl(\,\partial_x f,\;\partial_y f\bigr) = (2x,\;2y). \]

Evaluando en el punto \(\vec x_0 = (1,2)\):

\[ \nabla f(1,2) = (2\cdot1,\;2\cdot2) = (2,\;4) \]

La derivada direccional (sin normalizar) de \(f\) en la dirección de \(\vec v\) se expresa como:

\[ \frac{\partial f}{\partial \vec v}(\vec x_0) = \nabla f(\vec x_0)\;\cdot\;\vec v \]

Calculamos ahora el producto escalar entre \(\nabla f(1,2)\) y \(\vec v\):

\[ \frac{\partial f}{\partial \vec v}(1,2) = \nabla f(1,2)\cdot (3,4) \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = (2,4)\cdot(3,4) \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = 2\cdot3 + 4\cdot4 = 6 + 16 \]

\[ \frac{\partial f}{\partial \vec v}(1,2) = 22 \]

Este valor, 22, representa la variación de \(f\) en la dirección (no normalizada) de \((3,4)\).

Para obtener la derivada direccional unitaria, normalizamos el vector de dirección:

\[ \|\vec v\| = \sqrt{3^2 + 4^2} = 5, \qquad \hat v = \left(\tfrac{3}{5},\,\tfrac{4}{5}\right) \]

Así, la derivada direccional en la dirección del vector unitario \(\hat v\) resulta ser:

\[ D_{\hat v}f(1,2) = \nabla f(1,2)\cdot \hat v = (2,4)\cdot\left(\tfrac{3}{5},\tfrac{4}{5}\right) = \frac{1}{5}(2\cdot3 + 4\cdot4) \]

\[ = \frac{22}{5} = 4.4 \]

Por tanto, 4.4 es la tasa de variación de la función por unidad de longitud en esa dirección.

Este ejemplo ilustra con claridad cómo el gradiente permite obtener de manera inmediata la derivada direccional mediante el producto escalar con el vector de dirección elegido.

Para visualizar la función en tres dimensiones, la superficie definida por \( f(x, y) = x^2 + y^2 \) tiene la forma de un paraboloide, semejante a un cuenco orientado hacia arriba o a una cúpula invertida.

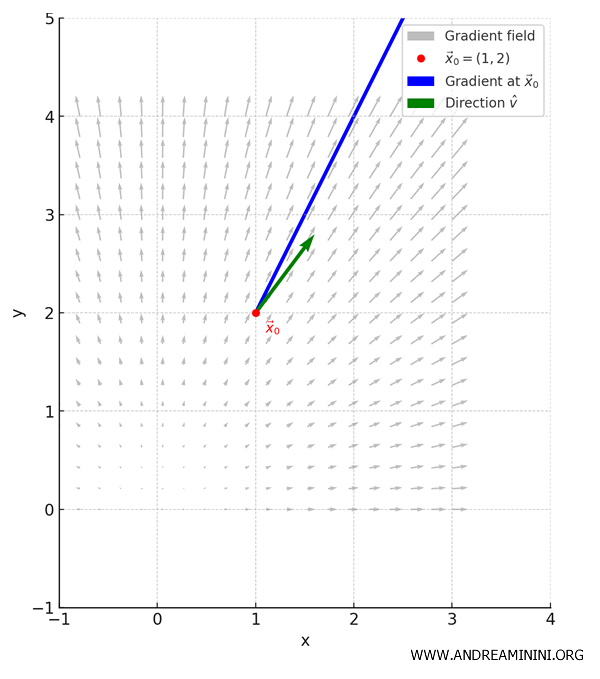
El punto rojo \( \vec{x}_0 = (1, 2) \) marca la posición concreta objeto de análisis.

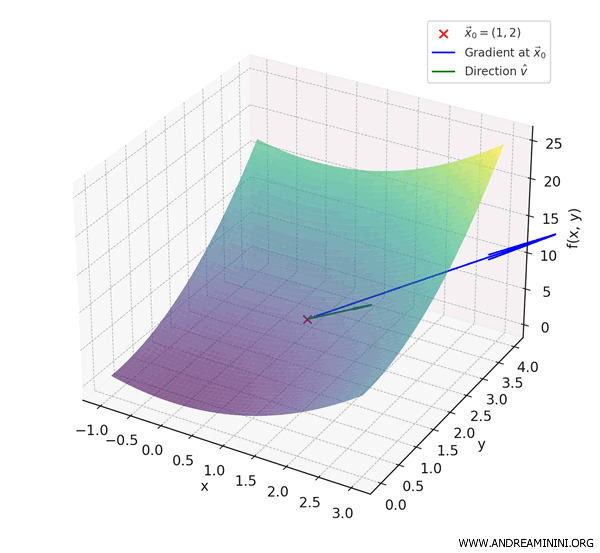
El vector azul representa el gradiente en \( \vec{x}_0 \); apunta en la dirección de crecimiento más pronunciado de la función.

El vector verde corresponde a la dirección unitaria \( \hat{v} \), que indica la tasa de incremento de la función al desplazarse en esa dirección.

Demostración

Queremos demostrar que, si \( f \) es diferenciable en \( \vec{x}_0 \), entonces la derivada direccional de \( f \) en \( \vec{x}_0 \) en la dirección de \( \vec{v} \) coincide con el producto escalar entre el gradiente \( \vec{\alpha} \) (la aproximación lineal de \( f \) en \( \vec{x}_0 \)) y el vector \( \vec{v} \):

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \]

Supongamos que \( f \) es diferenciable en \( \vec{x}_0 \). Por definición, esto implica que:

\[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \vec{\alpha} \cdot \vec{h} + o(|\vec{h}|) \quad \text{cuando } \vec{h} \to 0 \]

Se trata del desarrollo de Taylor de primer orden, en el que \( \vec{\alpha} \) es el gradiente de \( f \) en \( \vec{x}_0 \), y \( o(|\vec{h}|) \) representa un infinitésimo de orden superior, es decir, un término despreciable frente a \( |\vec{h}| \) cuando \( \vec{h} \to 0 \).

Sea ahora \( \vec{v} \) un vector unitario que fija una dirección. La derivada direccional de \( f \) en \( \vec{x}_0 \) a lo largo de \( \vec{v} \) se define como el límite:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) := \lim_{t \to 0} \frac{f(\vec{x}_0 + t\vec{v}) - f(\vec{x}_0)}{t} \]

Para evaluarlo, usamos la expansión de diferenciabilidad con \( \vec{h} = t\vec{v} \):

\[ f(\vec{x}_0 + t\vec{v}) = f(\vec{x}_0) + \vec{\alpha} \cdot (t\vec{v}) + o(|t\vec{v}|) \]

Sustituyendo en la definición obtenemos:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \lim_{t \to 0} \frac{f(\vec{x}_0 + t\vec{v}) - f(\vec{x}_0)}{t} \]

\[ = \lim_{t \to 0} \frac{f(\vec{x}_0) + t (\vec{\alpha} \cdot \vec{v}) + o(t|\vec{v}|) - f(\vec{x}_0)}{t} \]

Los términos constantes se cancelan, quedando:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \lim_{t \to 0} \frac{t (\vec{\alpha} \cdot \vec{v}) + o(t|\vec{v}|)}{t} \]

Factorizamos el numerador y separamos el límite:

\[ = \lim_{t \to 0} \left[ \vec{\alpha} \cdot \vec{v} + \frac{o(t|\vec{v}|)}{t} \right] \]

Por definición de la notación o-pequeña, \( \frac{o(t|\vec{v}|)}{t|\vec{v}|} \to 0 \) cuando \( t \to 0 \), de modo que el segundo término desaparece en el límite:

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\alpha} \cdot \vec{v} \]

Queda así demostrado que la derivada direccional se obtiene como el producto escalar entre el gradiente de \( f \) en \( \vec{x}_0 \) y el vector de dirección \( \vec{v} \).

Más ejemplos

Consideremos la función de dos variables \( f(x, y) = x^2 - xy \) y calculemos su derivada direccional en el punto \( (-1, 2) \) en la dirección del vector \( \mathbf{v} = (-1, 3) \).

Comenzamos calculando el gradiente \( \nabla f(x, y) \), es decir, el vector de derivadas parciales:

\[ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) \]

Las derivadas parciales de la función son:

• \( \frac{\partial f}{\partial x} = 2x - y \)
• \( \frac{\partial f}{\partial y} = -x \)

Por tanto, el gradiente es:

\[ \nabla f(x, y) = (2x - y, -x) \]

Evaluamos el gradiente en el punto \( (-1, 2) \) sustituyendo \( x = -1 \) y \( y = 2 \):

\[ \nabla f(-1, 2) = (2(-1) - 2, -(-1)) = (-2 - 2, 1) = (-4, 1) \]

Para calcular la derivada direccional, hacemos el producto escalar entre el gradiente \( (-4, 1) \) y el vector de dirección \( (-1, 3) \):

\[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \mathbf{v} = (-4, 1) \cdot (-1, 3) \]

\[ D_{\mathbf{v}}f(-1, 2) = (-4)(-1) + (1)(3) = 4 + 3 = 7 \]

El resultado, 7, es la derivada direccional de \( f \) en el punto \( (-1, 2) \) en la dirección de \( \mathbf{v} = (-1, 3) \).

Esto nos indica que, partiendo de \( (-1, 2, f(-1, 2)) = (-1, 2, 3) \) y avanzando en la dirección de \( \mathbf{v} \), la función aumenta a razón de 7: en términos geométricos, ascendemos por la superficie.

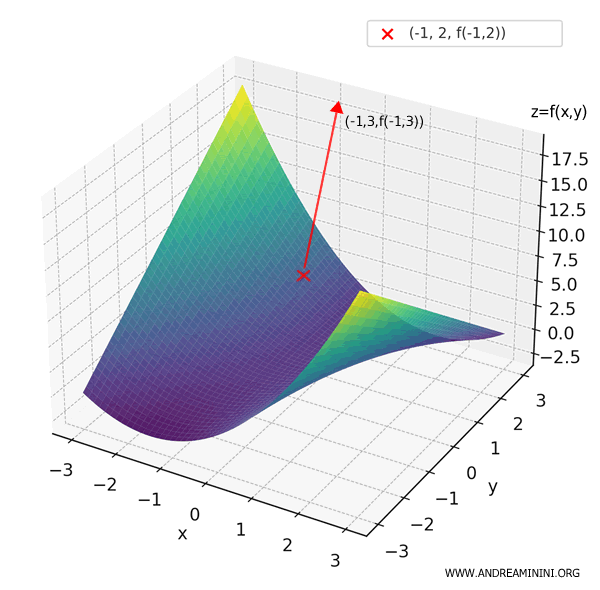
Para obtener la derivada direccional unitaria, normalizamos el vector de dirección dividiendo por su norma:

\[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \mathbf{v} }{ || \mathbf{v} ||} = \frac{ (-4, 1) \cdot (-1, 3) }{ \sqrt{1^2+3^2}  } \]

\[ D_{\mathbf{v}}f(-1, 2) = \frac{ 4 + 3 }{ \sqrt{10}  } = \frac{7}{\sqrt{10}} \approx 2.21 \]

Nota: La dirección en la que la función crece con mayor rapidez está dada por el propio gradiente, \( (-4, 1) \). En consecuencia, para ascender lo más empinado posible debemos movernos en esa dirección. \[ D_{\mathbf{v}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \nabla f(-1, 2) }{ || \nabla f(-1, 2) ||} = \frac{ (-4, 1) \cdot (-4, 1) }{ \sqrt{(-4)^2+1^2} } \] \[ D_{\mathbf{v}}f(-1, 2) = \frac{ 16 + 1 }{ \sqrt{17} } = \frac{17}{\sqrt{17}} = \sqrt{17} \approx 4.12 \]

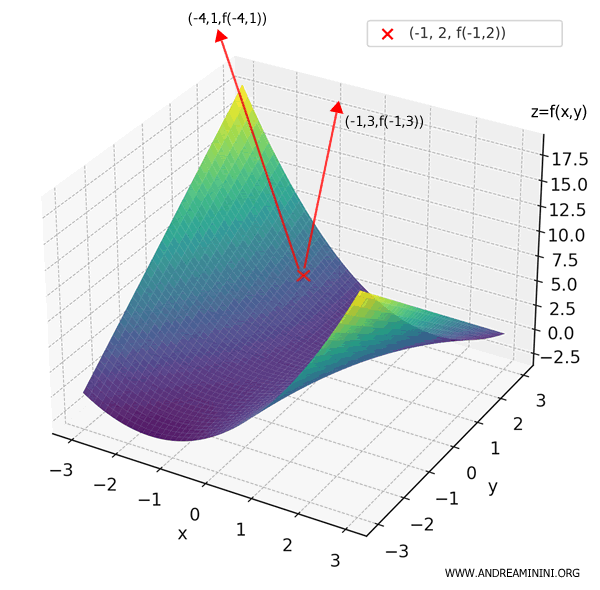
Ahora bien, ¿qué ocurre si nos desplazamos en otra dirección, por ejemplo \( \mathbf{w} = (1, 3) \), en lugar de \( \mathbf{v} = (-1, 3) \)?

El gradiente calculado antes permanece invariable:

\[ \nabla f(-1, 2) = (-4, 1) \]

Calculamos entonces el producto escalar entre el gradiente y el nuevo vector de dirección \( \mathbf{w} = (1, 3) \):

\[ D_{\mathbf{w}}f(-1, 2) = (-4, 1) \cdot (1, 3) = (-4)(1) + (1)(3) = -4 + 3 = -1 \]

El valor es negativo, lo que significa que \( D_{\mathbf{w}}f(-1, 2) = -1 \). Es decir, al movernos desde \( (-1, 2) \) en la dirección \( (1, 3) \), la función disminuye.

En otras palabras: avanzamos cuesta abajo sobre la superficie.

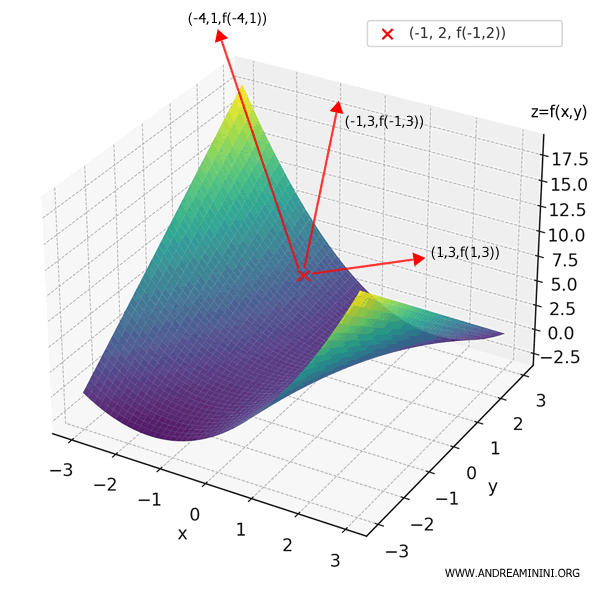
Por último, calculemos también la derivada direccional normalizada en esta dirección:

\[ D_{\mathbf{w}}f(-1, 2) = \nabla f(-1, 2) \cdot \frac{ \mathbf{w} }{ || \mathbf{w} || } = \frac{ (-4, 1) \cdot (1, 3) }{ \sqrt{1^2+3^2}  } \]

\[ D_{\mathbf{w}}f(-1, 2) = \frac{ -4 + 3 }{ \sqrt{10} } = \frac{ -1 }{ \sqrt{10} } \approx -0.316 \]

Esto nos permite comparar de forma directa las tasas de variación normalizadas en distintas direcciones.

Notas

Algunas observaciones complementarias que ayudan a entender mejor el concepto.

• Relación entre derivadas direccionales y parciales

  La derivada parcial de \( f \) respecto a \( x_k \) en el punto \( \vec{x}_0 \) coincide con la \(k\)-ésima componente del gradiente de \( f \) evaluado en ese punto.

  En otras palabras, las derivadas parciales son un caso particular de derivadas direccionales: corresponden a tomar como vector de dirección uno de los vectores de la base canónica, es decir, \( \vec{e}_k \), que tiene un 1 en la posición \(k\) y ceros en el resto. Por ejemplo, en \( \mathbb{R}^3 \): \[ \vec{e}_1 = (1, 0, 0), \quad \vec{e}_2 = (0, 1, 0), \quad \vec{e}_3 = (0, 0, 1) \] Así, la derivada parcial respecto a \( x_k \) se puede escribir como derivada direccional en la dirección \( \vec{e}_k \): \[ \frac{\partial f}{\partial x_k}(\vec{x}_0) = \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) \] Según la definición de derivada direccional: \[ \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) = \vec{\alpha} \cdot \vec{e}_k \] donde \( \vec{\alpha} = \nabla f(x_0) \). El producto escalar con \( \vec{e}_k \) extrae precisamente la componente \(k\)-ésima del gradiente: \[ \frac{\partial f}{\partial \vec{e}_k}(\vec{x}_0) = \alpha_k \] De este modo, la derivada parcial de \( f \) respecto a \( x_k \) en \( \vec{x}_0 \) coincide exactamente con la componente \(k\)-ésima del gradiente. Es decir, si \( \vec{v} = \vec{e}_k \), la derivada direccional reproduce la parcial correspondiente.

  Ejemplo. Consideremos la función: \[ f(x, y) = 3x^2y + 2y \] Sus derivadas parciales son: \[ \frac{\partial f}{\partial x} = 6xy, \quad \frac{\partial f}{\partial y} = 3x^2 + 2 \] De modo que el gradiente es: \[ \nabla f(x, y) = \left( 6xy,\ 3x^2 + 2 \right) \] Evaluando en el punto \( (1, 2) \): \[ \nabla f(1, 2) = (6 \cdot 1 \cdot 2,\ 3 \cdot 1^2 + 2) = (12,\ 5) \] La derivada parcial respecto a \( x \) en \( (1, 2) \) es: \[ \frac{\partial f}{\partial x}(1, 2) = 6 \cdot 1 \cdot 2 = 12 \] Consideremos ahora la derivada direccional en la dirección de \( \vec{e}_1 = (1, 0) \). Aplicando la fórmula: \[ \frac{\partial f}{\partial \vec{e}_1}(1, 2) = \nabla f(1, 2) \cdot \vec{e}_1 = (12,\ 5) \cdot (1,\ 0) = 12 \] Esto confirma que la derivada parcial coincide con la derivada direccional en la dirección de un vector de la base canónica: \[ \frac{\partial f}{\partial x}(1, 2) = 12 \quad \text{y} \quad \nabla f(1, 2) \cdot \vec{e}_1 = 12 \] La figura siguiente representa el campo vectorial de gradientes normalizados.
  

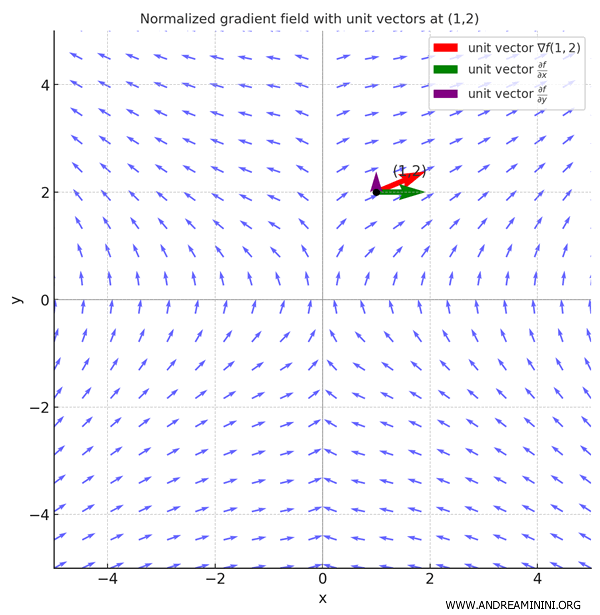
• El gradiente como vector de máximo incremento

  El gradiente \( \nabla f(x_0) \) es el vector que apunta en la dirección donde la función crece con mayor rapidez.

  Su magnitud indica la velocidad con la que aumenta en esa dirección.

  Demostración. Partimos de la expresión de la derivada direccional de \( f \) en el punto \( x_0 \) en la dirección de un vector \( \vec{v} \): \[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \] Al ser un producto escalar, puede escribirse como el producto de las normas de ambos vectores y el coseno del ángulo \( \theta \) que forman: \[ \frac{\partial f}{\partial \vec{v}}(x_0) = |\nabla f(x_0)| \cdot |\vec{v}| \cdot \cos\theta \] Esta fórmula muestra que la derivada direccional depende de la magnitud del gradiente \( |\nabla f(x_0)| \), de la longitud del vector de dirección \( |\vec{v}| \) (que normalmente se toma unitario, \( |\vec{v}| = 1 \)), y sobre todo del coseno del ángulo \( \theta \) entre \( \nabla f \) y \( \vec{v} \). La interpretación geométrica se apoya precisamente en el comportamiento del coseno.

  • Cuando \( \cos \theta = 1 \), es decir, \( \theta = 0^\circ \), los vectores están alineados. La derivada direccional es máxima en la dirección del gradiente.
  • Cuando \( \cos \theta = -1 \), es decir, \( \theta = 180^\circ \), los vectores apuntan en sentidos opuestos. La derivada direccional es mínima en la dirección contraria al gradiente.
  • Cuando \( \cos \theta = 0 \), es decir, \( \theta = 90^\circ \), los vectores son ortogonales. En este caso, la derivada direccional vale cero: la función no varía en esa dirección.

  De este modo se confirma que el gradiente \( \nabla f(x_0) \) señala la dirección de ascenso más pronunciado y que su magnitud refleja la rapidez con la que la función aumenta en ella.

Pueden elaborarse más ejemplos e interpretaciones siguiendo este mismo razonamiento.

Así es, en esencia.