Gradiente

El gradiente de una función o campo escalar f(x, y, z) es un campo vectorial cuyas componentes son las derivadas parciales de f con respecto a las coordenadas cartesianas (x, y, z). $$ \nabla f = \frac{ \partial f}{\partial x} \vec{u}_x + \frac{ \partial f}{\partial y} \vec{u}_y + \frac{ \partial f}{\partial z} \vec{u}_z $$ Este operador diferencial, representado por el símbolo nabla ∇ (un triángulo invertido), también se suele denotar como grad: $$ \text{grad} \, f = \frac{ \partial f}{ \partial x} \vec{u}_x + \frac{ \partial f}{ \partial y} \vec{u}_y + \frac{ \partial f}{ \partial z} \vec{u}_z $$

Aquí, u_x, u_y y u_z son los vectores unitarios que apuntan a lo largo de los ejes x, y y z del espacio tridimensional.

El campo escalar f(x, y, z) es una función de valores reales.

En cambio, el gradiente ∇f es una función vectorial.

¿Qué representa el gradiente?

El gradiente transforma un campo escalar en un campo vectorial. Proporciona tanto la dirección como la magnitud del cambio más pronunciado de la cantidad escalar.

Por ejemplo, el gradiente de temperatura indica cómo y en qué dirección varía más rápidamente la temperatura en el espacio.

Nota. El gradiente señala la dirección en la que el campo escalar f(x, y, z) crece con mayor rapidez. Su módulo indica la velocidad máxima de variación en ese punto.

Propiedades fundamentales del gradiente

Dado un gradiente ∇f y un vector v, el producto escalar ∇f · v proporciona la derivada direccional de f en la dirección de v:

$$ \nabla f \cdot \vec{v} = D_v f $$

¿Qué es una derivada direccional? La derivada direccional mide cómo varía una función f(x, y, z) al desplazarnos en una dirección concreta, determinada por el vector v: $$ D_v f = \lim_{h \to 0} \frac{f(x+h \cdot \vec{v}, \ y+h \cdot \vec{v}, \ z+h \cdot \vec{v}) - f(x, y, z)}{h} $$ Generaliza el concepto de derivada parcial, que solo mide la variación a lo largo de los ejes coordenados: $$ D_x f = \lim_{\Delta x \to 0} \frac{f(x+\Delta x, y, z) - f(x, y, z)}{\Delta x} $$

Si consideramos un desplazamiento infinitesimal en la dirección del vector de posición v (vector de posición):

$$ d \vec{v} = dx \cdot \vec{u}_x + dy \cdot \vec{u}_y + dz \cdot \vec{u}_z $$

La derivada direccional de f en esta dirección se expresa mediante el gradiente:

$$ \frac{d \ f(\vec{v})}{d \ \vec{v}} = \nabla f $$

Por tanto, el diferencial de la función en la dirección de v es:

$$ df(\vec{v}) = \nabla f \cdot d \vec{v} $$

En consecuencia, el valor de la función en un punto cercano se puede aproximar así:

$$ f(\vec{v} + d \vec{v}) = f(\vec{v}) + df(\vec{v}) = f(\vec{v}) + \nabla f(\vec{v}) \cdot \vec{v} $$

Un ejemplo concreto

Consideremos una función de dos variables:

\[ f(x, y) = x^2 + y^2 \]

Esta función asigna a cada punto \( (x, y) \) el cuadrado de su distancia al origen.

Para calcular el gradiente \( \nabla f \), derivamos parcialmente con respecto a \( x \) y \( y \):

\[ \frac{\partial f}{\partial x} = 2x \]

\[ \frac{\partial f}{\partial y} = 2y \]

Por lo tanto, el gradiente se expresa como:

\[ \nabla f(x, y) = 2x \, \vec{u}_x + 2y \, \vec{u}_y \]

En notación vectorial:

\[ \nabla f(x, y) = \begin{pmatrix} 2x \\ 2y \end{pmatrix} \]

Los vectores del gradiente apuntan radialmente hacia el exterior desde el origen. Esto refleja que la función \( f(x, y) = x^2 + y^2 \) crece con mayor rapidez en la dirección radial.

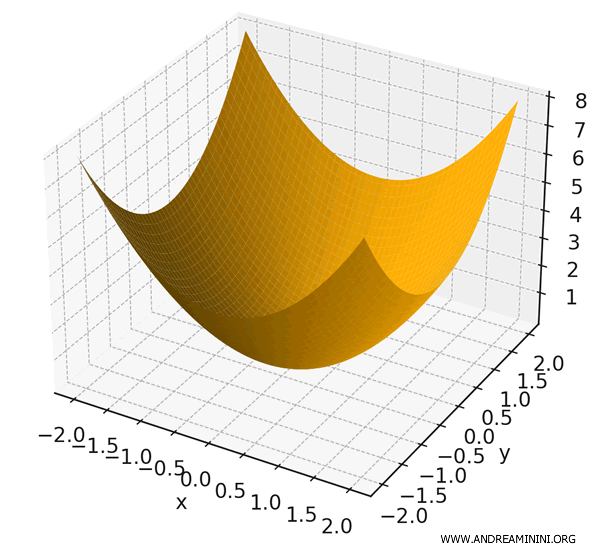
La magnitud del gradiente es \( |\nabla f| = \sqrt{(2x)^2 + (2y)^2} = 2\sqrt{x^2 + y^2} \), que representa la rapidez con la que aumenta la función al alejarse del origen.

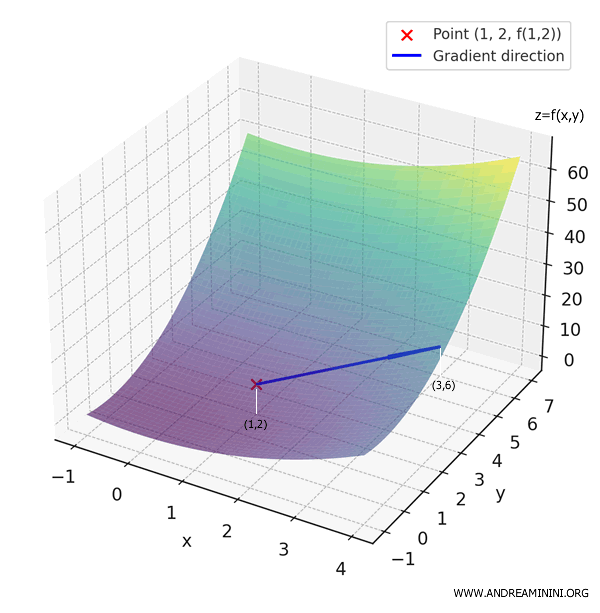
Por ejemplo, en el punto \( (1, 2) \):

\[ \nabla f(1, 2) = \begin{pmatrix} 2 \cdot 1 \\ 2 \cdot 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} \]

Esto significa que en \( (1, 2) \), la función aumenta más rápidamente en la dirección del vector \( (2, 4) \), que apunta hacia el punto \( (3, 6) \).

Este análisis puede repetirse en cualquier punto del plano \( (x, y) \).

El resultado es el campo vectorial del gradiente de la función \( f(x, y) = x^2 + y^2 \):

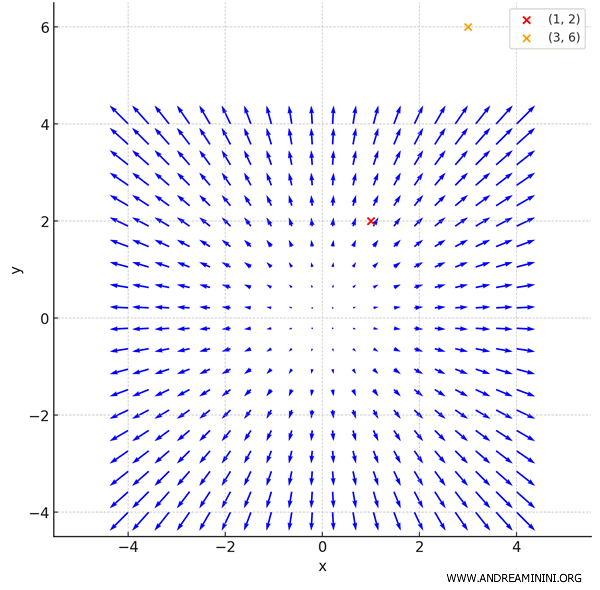
Cada flecha representa el vector gradiente en un punto específico \( (x, y) \).

Todos los vectores apuntan hacia el exterior, ya que la función crece con la distancia al origen.

Los puntos \( (1, 2) \) y \( (3, 6) \) están marcados en rojo y en naranja, respectivamente.

También se pueden añadir curvas de nivel, que representan los lugares geométricos donde la función alcanza un valor constante \( f(x, y) = c \).

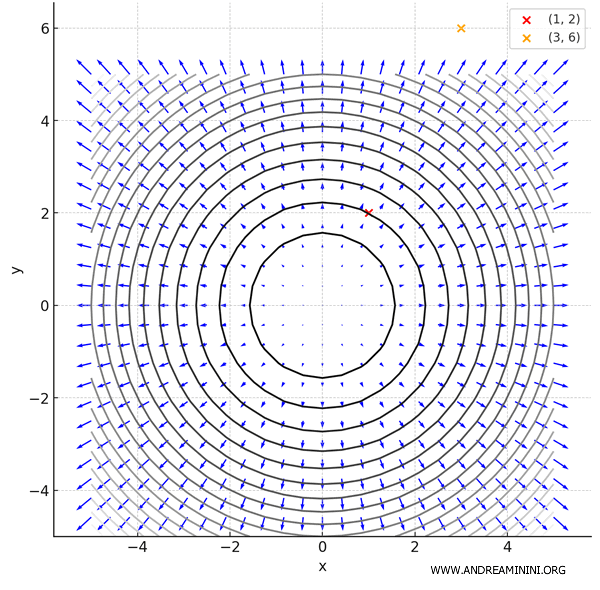
En este caso, las curvas de nivel son círculos concéntricos, dado que \( f(x, y) = x^2 + y^2 \).

El gradiente señala la dirección de máximo aumento

El gradiente \( \nabla f(x_0) \) es un vector que indica la dirección en la que la función crece con mayor rapidez.

Dicho de otro modo, el gradiente apunta hacia la dirección de ascenso más pronunciado, es decir, el camino a lo largo del cual la función experimenta la mayor tasa de incremento.

La magnitud del gradiente cuantifica precisamente dicha tasa de variación en esa dirección.

Por el contrario, la dirección de descenso más pronunciado corresponde al vector gradiente con signo negativo.

Ejemplo

Consideremos la siguiente función:

$$ f(x,y) = x^2 + y^2 $$

Se trata de la ecuación de una superficie con forma de cuenco, un ejemplo clásico que ya hemos visto anteriormente.

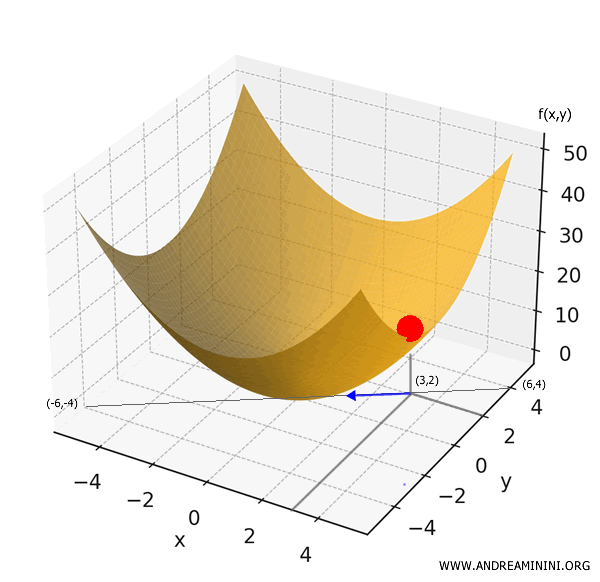
Supongamos que dejamos caer una bola en el punto (3,2). ¿En qué dirección empezará a rodar?

Para responder, primero calculamos las derivadas parciales de la función respecto a \( x \) y \( y \):

$$ f_x = 2x $$

$$ f_y = 2y $$

Con estas expresiones podemos construir el vector gradiente de la función:

$$ \nabla f(x,y) = (2x, 2y) $$

Evaluando el gradiente en el punto (3,2) obtenemos:

$$ \nabla f(3,2) = (2 \cdot 3, 2 \cdot 2) = (6, 4) $$

El vector gradiente siempre apunta en la dirección de máximo aumento de la función, es decir, hacia donde esta crece más rápidamente.

No obstante, como la bola está sometida a la gravedad, rodará cuesta abajo, en la dirección en la que la función disminuye más rápidamente. Esta dirección es exactamente opuesta al gradiente:

$$ -\nabla f(3,2) = (-6, -4) $$

Por lo tanto, la bola se desplazará siguiendo la dirección del vector \( (-6, -4) \).

Nota. También es posible normalizar este vector direccional para obtener un vector unitario que apunte en la misma dirección: \[ \mathbf{u} = \frac{-\nabla f(3,2)}{\lVert \nabla f(3,2) \rVert} = \frac{(-6, -4)}{\sqrt{6^2 + 4^2}} = \Bigl(-\tfrac{3}{\sqrt{13}},\, -\tfrac{2}{\sqrt{13}}\Bigr) \] Al dividir por la magnitud del gradiente obtenemos un vector de módulo uno, lo cual resulta útil para describir únicamente la dirección, sin depender de la velocidad ni de la pendiente. La interpretación geométrica y física permanece inalterada.

Demostración

Para demostrar este hecho, partimos de la definición de la derivada direccional de una función \( f \) en el punto \( x_0 \), en la dirección de un vector \( \vec{v} \).

La derivada direccional se expresa como el producto escalar entre el gradiente de \( f \) en \( x_0 \) y el vector direccional \( \vec{v} \):

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \nabla f(x_0) \cdot \vec{v} \]

Utilizando la definición geométrica del producto escalar, esta expresión se puede reescribir como:

\[ \frac{\partial f}{\partial \vec{v}}(x_0) = |\nabla f(x_0)| \cdot |\vec{v}| \cdot \cos\theta \]

Aquí, \( \theta \) es el ángulo que forman el gradiente \( \nabla f(x_0) \) y el vector de dirección \( \vec{v} \).

Esta fórmula muestra que el valor de la derivada direccional depende de tres factores clave:

1. La magnitud del gradiente, que indica cuán rápidamente varía la función en ese punto;
2. La longitud del vector direccional \( \vec{v} \), que habitualmente se normaliza para que \( |\vec{v}| = 1 \);
3. El coseno del ángulo entre el gradiente y el vector de dirección.

Dado que la magnitud del gradiente es independiente de la dirección elegida y que el vector direccional suele tener módulo uno, la derivada direccional varía fundamentalmente en función del coseno del ángulo \( \theta \).

Veamos cómo afecta el valor de \( \cos\theta \) a la derivada direccional según diferentes valores de \( \theta \):

• Si \( \theta = 0^\circ \), entonces \( \cos\theta = 1 \): los vectores están alineados y apuntan en la misma dirección. La derivada direccional alcanza su valor máximo, coincidiendo con la dirección del gradiente.
• Si \( \theta = 180^\circ \), entonces \( \cos\theta = -1 \): los vectores son paralelos pero de sentido opuesto. La derivada direccional alcanza su valor mínimo, en la dirección contraria al gradiente.
• Si \( \theta = 90^\circ \), entonces \( \cos\theta = 0 \): los vectores son ortogonales. La derivada direccional es cero, lo que significa que la función no varía en esa dirección.

Este análisis confirma que el gradiente \( \nabla f(x_0) \) no solo indica la dirección de máximo crecimiento, sino que su magnitud representa también la tasa máxima de variación de la función en dicho punto.

Relación entre el gradiente y las curvas de nivel

El gradiente es siempre perpendicular a las curvas de nivel.

Esto significa que si trazamos una curva de nivel - por ejemplo, un círculo - , el gradiente en cualquier punto de dicha curva es un vector ortogonal a ella, que apunta radialmente hacia el exterior.

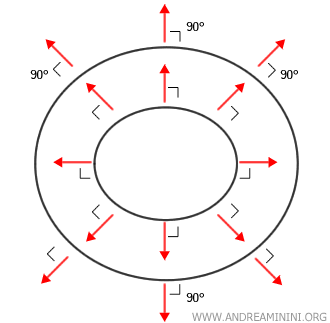
Las curvas de nivel representan el conjunto de puntos donde la función adopta un valor constante, es decir, $ f(x,y) = c $.

Por su parte, el gradiente señala la dirección de máximo aumento: $ \nabla f(x, y) = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) $.

Así, si la función permanece constante en una dirección (a lo largo de una curva de nivel) y aumenta con mayor rapidez en otra (en la dirección del gradiente), estas direcciones han de ser perpendiculares: forman un ángulo recto.

Ejemplo

El gradiente de la función $ f(x,y) = x^2 + y^2 $ define un campo vectorial que asigna, a cada punto del plano, un vector que apunta en la dirección de máximo aumento, y en sentido contrario, en la de mayor descenso.

Como se aprecia, el vector gradiente en cualquier punto $ (x,y,z) $ de la superficie definida por $ z = f(x,y) $ es perpendicular a la curva de nivel que pasa por dicho punto.

El único punto donde el gradiente se anula es el origen, $ (x,y,z) = (0,0,0) $, centro de las curvas de nivel de esta función: allí el vector no tiene dirección.

Nota. Un gradiente nulo indica la presencia de un punto crítico: un punto donde la función no varía en ninguna dirección. En tales casos, es útil calcular el laplaciano, definido como la suma de las segundas derivadas parciales respecto a las variables espaciales: \[\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\] El valor del laplaciano en ese punto permite caracterizar la naturaleza del punto crítico: si \( \Delta f > 0 \), se trata de un mínimo local; si \( \Delta f < 0 \), de un máximo local; y si \( \Delta f = 0 \), el resultado es inconcluso y requiere un análisis adicional.

Demostración

Sea \( (x_0, y_0) \) un punto del dominio de \( f \), y consideremos una curva suave \( \gamma(t) = (x(t), y(t)) \) que se mantiene contenida en una curva de nivel de \( f \).

Dado que el valor de la función permanece constante a lo largo de esta curva, su derivada direccional debe ser nula:

\[ f(x(t), y(t)) = \text{constante} \quad \Rightarrow \quad \frac{d}{dt} f(x(t), y(t)) = 0 \]

Aplicando la regla de la cadena obtenemos:

\[ \frac{d}{dt} f(x(t), y(t)) = \frac{\partial f}{\partial x} \cdot \frac{dx}{dt} + \frac{\partial f}{\partial y} \cdot \frac{dy}{dt} = \nabla f \cdot \vec{v} = 0 \]

Aquí, \( \vec{v} = \left( \frac{dx}{dt}, \frac{dy}{dt} \right) \) es el vector tangente a la curva \( \gamma(t) \).

Como el producto escalar \( \nabla f \cdot \vec{v} = 0 \), el gradiente \( \nabla f \) es ortogonal al vector tangente; es decir, es perpendicular a la curva de nivel.

Y así sucesivamente.