Conjunto acotado en $ \mathbb{R}^2 $ (el plano)

Un conjunto $ A $ en el plano cartesiano $ \mathbb{R}^2 $ se denomina conjunto acotado si existe una circunferencia suficientemente grande, centrada en el origen (el punto $ (0,0) $), que contenga por completo a $ A $.

En términos formales, existe un número $ M > 0 $ tal que, para todo punto $ (x,y) $ de $ A $, la distancia al origen, calculada como $ \sqrt{x^2 + y^2} $, es siempre menor o igual que $ M $.

$$ \sqrt{x^2 + y^2} \le M $$

En otras palabras, $ A $ queda contenido en una circunferencia de radio $ M $ centrada en el origen.

Si se puede encontrar tal valor de $ M $, decimos que el conjunto $ A $ es acotado.

Si no existe ningún $ M $ con esta propiedad, entonces $ A $ es no acotado.

Un ejemplo práctico

Consideremos el conjunto de puntos $ A = \{ (1, 2), (2, 3), (3, 1), (1, -1) \} $ en el plano cartesiano.

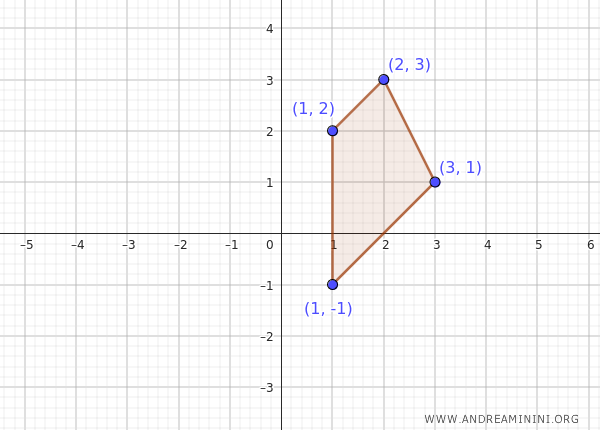
Ejemplo práctico de un conjunto finito

Queremos determinar si este conjunto es acotado.

Para ello basta comprobar si existe una circunferencia centrada en el origen que incluya a todos los puntos de $ A $.

Calculemos la distancia de cada punto al origen:

Para $ (1, 2) $: $$ \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5} \approx 2.24 $$
Para $ (2, 3) $: $$ \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \approx 3.61 $$
Para $ (3, 1) $: $$ \sqrt{3^2 + 1^2} = \sqrt{9 + 1} = \sqrt{10} \approx 3.16 $$
Para $ (1, -1) $: $$ \sqrt{1^2 + (-1)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.41 $$

La mayor de estas distancias es $ \sqrt{13} \approx 3.61 $.

Esto significa que todos los puntos de $ A $ quedan dentro de una circunferencia de radio $ M = \sqrt{13} \approx 3.61 $, centrada en el origen.

$$ \sqrt{ x^2 + y^2 } \le \sqrt{13} $$

Como existe un valor de $ M $ que cumple esta condición, concluimos que el conjunto $ A $ es acotado.

En otras palabras, todos los puntos de $ A $ se encuentran en el interior de una circunferencia centrada en el origen y de radio $ \sqrt{13} $.

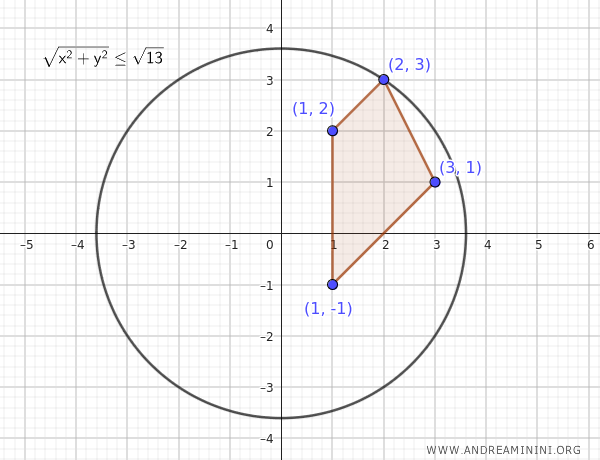
Ejemplo de un conjunto acotado

Este ejemplo ilustra de forma clara y sencilla cómo verificar si un conjunto de puntos en el plano es acotado.

Nota: Si consideramos un conjunto cuyos puntos se extienden indefinidamente lejos del origen -por ejemplo, todos los puntos de una recta que no pase por el origen-, no sería posible hallar una circunferencia que los contenga a todos, y en ese caso el conjunto sería no acotado.

Y así sucesivamente.

Conjunto acotado en \( \mathbb{R}^2 \) (el plano)

Un ejemplo práctico