Diferenciabilidad de una función de dos variables

Sea \( f: \mathbb{R}^2 \to \mathbb{R} \) una función real de dos variables. Decimos que \( f \) es diferenciable en el punto \( (x_0, y_0) \in \mathbb{R}^2 \) si existen dos números reales \( \alpha \) y \( \beta \) tales que: \[ f(x_0 + h,\ y_0 + k) = f(x_0, y_0) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \] 

En esta expresión:

• \( h \) y \( k \) representan pequeños desplazamientos a lo largo de los ejes \( x \) e \( y \)
• \( \sqrt{h^2 + k^2} \) es la distancia euclídea entre el punto \( (x_0, y_0) \) y el punto perturbado \( (x_0 + h, y_0 + k) \)
• \( o\left(\sqrt{h^2 + k^2}\right) \) denota un infinitésimo de orden superior, es decir, un término de error que tiende a cero más rápido que el propio desplazamiento

Si \( f \) es diferenciable en \( (x_0, y_0) \), entonces existen las derivadas parciales en dicho punto y se cumple que:

\[ \alpha = \frac{\partial f}{\partial x}(x_0, y_0) \]

\[ \beta = \frac{\partial f}{\partial y}(x_0, y_0) \]

De este modo, la fórmula de diferenciabilidad puede reescribirse como:

\[ f(x_0 + h, y_0 + k) = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0) \cdot h + \frac{\partial f}{\partial y}(x_0, y_0) \cdot k + o\left(\sqrt{h^2 + k^2}\right) \]

Recordemos que el gradiente de \( f \) en el punto \( (x_0, y_0) \) está formado por las derivadas parciales evaluadas en ese punto:

\[ \nabla f(x_0, y_0) = \left( \frac{\partial f}{\partial x}(x_0, y_0),\ \frac{\partial f}{\partial y}(x_0, y_0) \right) \]

Con esta notación, la aproximación de primer orden de la función en un punto próximo \( (x_0 + h,\ y_0 + k) \) se expresa como:

\[ f(x_0 + h,\ y_0 + k) = f(x_0,\ y_0) + \nabla f(x_0,\ y_0) \cdot (h,\ k) + o\left( \sqrt{h^2 + k^2} \right) \]

Si denotamos el vector de desplazamiento como \( \vec{h} = (h,\ k) \) y el punto de referencia como \( \vec{x}_0 = (x_0,\ y_0) \), la expresión adquiere una forma más compacta en notación vectorial:

\[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \nabla f(\vec{x}_0) \cdot \vec{h} + o(\|\vec{h}\|) \]

De manera intuitiva, una función \( f(x, y) \) es diferenciable en un punto si, en un entorno de ese punto, se comporta localmente como un plano.

En otras palabras, la función puede aproximarse en las proximidades mediante un plano tangente.

Esta es una condición mucho más exigente que la mera existencia de derivadas parciales, ya que garantiza un comportamiento suave y regular de la función en torno al punto considerado.

Nota. El símbolo \( o\left(\sqrt{h^2 + k^2}\right) \) representa el siguiente límite: \[ \lim_{(h, k) \to (0, 0)} \frac{o\left(\sqrt{h^2 + k^2}\right)}{\sqrt{h^2 + k^2}} = 0 \] Es decir, el término de error resulta insignificante en comparación con \( \sqrt{h^2 + k^2} \) cuando \((h, k)\) tiende a \((0, 0)\). Esta condición asegura que el comportamiento local de la función sea lineal en primera aproximación.

¿Cómo comprobar si una función es diferenciable en un punto?

En la práctica, el teorema del diferencial total es la herramienta más eficaz para determinar la diferenciabilidad en un punto, ya que proporciona un criterio más directo y elegante que la definición formal.

Un ejemplo práctico

Consideremos la función:

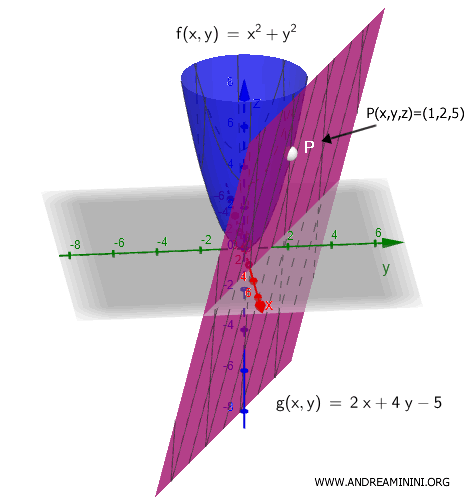
\[ f(x, y) = x^2 + y^2 \]

Queremos verificar si esta función es diferenciable en el punto \( (x_0, y_0) = (1, 2) \).

Sustituyendo estas coordenadas en la fórmula de diferenciabilidad obtenemos:

\[ f(x_0 + h,\ y_0 + k) = f(x_0, y_0) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

\[ f(1 + h,\ 2 + k) = f(1, 2) + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

Como \( f(1, 2) = 1^2 + 2^2 = 5 \), resulta:

\[ f(1 + h,\ 2 + k) = 5 + \alpha h + \beta k + o\left(\sqrt{h^2 + k^2}\right) \]

Aquí, \(\alpha\) y \(\beta\) son las derivadas parciales de la función en \( (1, 2) \):

\[ \alpha = \frac{\partial f}{\partial x}(1, 2) = 2x = 2 \cdot 1 = 2 \]

\[ \beta = \frac{\partial f}{\partial y}(1, 2) = 2y = 2 \cdot 2 = 4 \]

Nota. Los valores \(\alpha\) y \(\beta\) corresponden exactamente a los coeficientes del plano tangente en el punto \((x_0, y_0)\). Indican la inclinación de la superficie en cada dirección, de manera análoga a cómo la recta tangente refleja la variación local en el cálculo de una sola variable.

Así, los coeficientes del plano tangente en \( (x_0, y_0) = (1, 2) \) son \( \alpha = 2 \) y \( \beta = 4 \):

\[ f(1 + h, 2 + k) = 5 + 2h + 4k + o\left(\sqrt{h^2 + k^2}\right) \]

Consideremos ahora pequeños desplazamientos \( h \) y \( k \) a partir del punto \( (1, 2) \).

Por ejemplo, si \( h = 0.01 \) y \( k = -0.02 \), la aproximación lineal nos da:

\[ f(1.01, 1.98) \approx 5 + 2 \cdot 0.01 + 4 \cdot (-0.02) = 5 + 0.02 - 0.08 = 4.94 \]

El término de orden superior \( o(\cdot) \) es despreciable, por lo que se omite.

El valor exacto de la función resulta prácticamente igual a 4.94, con un error irrelevante (4.94 ≈ 5).

¿Cuál es la ecuación del plano tangente?

La fórmula general del plano tangente es:

\[ z = f(x_0, y_0) + \frac{\partial f}{\partial x}(x_0, y_0) \cdot (x - x_0) + \frac{\partial f}{\partial y}(x_0, y_0) \cdot (y - y_0) \]

Como \( (x_0, y_0) = (1, 2) \) y \( f(1, 2) = 5 \), se obtiene:

\[ z = 5 + \frac{\partial f}{\partial x}(1, 2) \cdot (x - 1) + \frac{\partial f}{\partial y}(1, 2) \cdot (y - 2) \]

Las derivadas parciales son \( \frac{\partial f}{\partial x}(1, 2) = 2 \) y \( \frac{\partial f}{\partial y}(1, 2) = 4 \), luego:

\[ z = 5 + 2(x - 1) + 4(y - 2) \]

\[ z = 5 + 2x - 2 + 4y - 8 \]

\[ z = 2x + 4y - 5 \]

Esta es la ecuación del plano \( g(x, y) = 2x + 4y - 5 \), que aproxima localmente la superficie de la función \( f(x, y) = x^2 + y^2 \) en el punto \( P(x_0, y_0, z) = (1, 2, 5) \).

Diferenciabilidad en funciones de n variables

La diferenciabilidad en \( \mathbb{R}^n \) se formula de manera más clara y elegante mediante la notación vectorial:

Una función \( f : \mathbb{R}^n \to \mathbb{R} \) es diferenciable en un punto \( \vec{x}_0 \in \mathbb{R}^n \) si existe un vector \( \vec{\alpha} \in \mathbb{R}^n \) tal que: \[ f(\vec{x}_0 + \vec{h}) = f(\vec{x}_0) + \vec{\alpha} \cdot \vec{h} + o(\|\vec{h}\|) \quad \text{cuando } \vec{h} \to \vec{0} \]

Donde:

• \( \vec{x}_0 \) es el vector de posición del punto en el que se estudia la diferenciabilidad
• \( \vec{h} \) es el vector incremento, es decir, un desplazamiento a partir de \( \vec{x}_0 \)
• \( \vec{\alpha} \) es el gradiente de la función en \( \vec{x}_0 \)
• \( \vec{\alpha} \cdot \vec{h} \) es el producto escalar, que constituye la parte lineal de la aproximación
• \( o(\|\vec{h}\|) \) es el término de error, que tiende a cero más rápidamente que \( \|\vec{h}\| \)

La condición \( \vec{h} \to \vec{0} \) significa que nos aproximamos a \( \vec{x}_0 \) desde todas las direcciones posibles.

Si \( f \) es diferenciable en \(\vec{x}_0\), entonces existen todas sus derivadas parciales en ese punto.

¿Cómo se calcula una derivada direccional?

Si una función \( f \) es diferenciable en un punto \( \vec{x}_0 \), entonces la derivada direccional de \( f \) en la dirección de un vector \( \vec{v} \) viene dada por el producto escalar entre el gradiente de \( f \) en ese punto y el vector de dirección \( \vec{v} \):

\[ \frac{\partial f}{\partial \vec{v}}(\vec{x}_0) = \vec{\nabla}f(x_0) \cdot \vec{v} \]

Aquí, \( \vec{v} \) es el vector de dirección y \( \vec{\nabla}f(x_0) \) representa el gradiente de la función en el punto \(\vec{x}_0\).

Teorema del diferencial total

Sea \( f(x, y) \) una función definida en un entorno de un punto \( (x_0, y_0) \in \mathbb{R}^2 \). Si las derivadas parciales \( f_x \) y \( f_y \) existen en ese entorno y son continuas en el punto, entonces \( f \) es diferenciable en \( (x_0, y_0) \).

En tal caso, el diferencial total de \( f \) en \( (x_0, y_0) \) se escribe:

\[ df = f_x(x_0, y_0) \, dx + f_y(x_0, y_0) \, dy \]

Lo que nos proporciona una aproximación lineal de la función cerca del punto:

\[ f(x, y) \approx f(x_0, y_0) + f_x(x_0, y_0)(x - x_0) + f_y(x_0, y_0)(y - y_0) \]

El teorema del diferencial total es especialmente útil porque permite establecer la diferenciabilidad en un punto sin recurrir a la definición formal, mucho más técnica y laboriosa.

Nota. Este teorema proporciona una condición suficiente -aunque no necesaria- de diferenciabilidad. Es decir, si las derivadas parciales existen en un entorno de un punto y son continuas en él, entonces la función es diferenciable allí. Sin embargo, puede ocurrir que una función sea diferenciable en un punto aunque sus derivadas parciales no sean continuas en dicho punto.

Ejemplo

Consideremos de nuevo la función del ejemplo anterior:

\[ f(x, y) = x^2 + y^2 \]

Queremos comprobar que \( f \) es diferenciable en el punto \( (1, 2) \) aplicando el teorema del diferencial total.

Las derivadas parciales de la función son:

\[ f_x(x, y) = \frac{\partial}{\partial x}(x^2 + y^2) = 2x \\ f_y(x, y) = \frac{\partial}{\partial y}(x^2 + y^2) = 2y \]

Dado que \( f_x(x, y) = 2x \) y \( f_y(x, y) = 2y \) son polinomios, resultan continuos en todo \( \mathbb{R}^2 \).

Por tanto, las derivadas parciales son continuas en un entorno de \( (1, 2) \).

En consecuencia, por el teorema del diferencial total, la función es diferenciable en \( (1, 2) \).

Para completar la verificación, calculemos el diferencial total en \( (1, 2) \):

\[ df = f_x(1, 2) \, dx + f_y(1, 2) \, dy = 2 \cdot 1 \cdot dx + 2 \cdot 2 \cdot dy = 2dx + 4dy \]

De este modo disponemos de un criterio rápido y fiable para determinar la diferenciabilidad en un punto, sin necesidad de recurrir a la definición formal.

Nota. En este caso concreto, la continuidad de las derivadas parciales es inmediata, pues se trata de polinomios. En general, sin embargo, comprobar la continuidad exige demostrar que el límite existe y coincide con el valor de la derivada en el punto. Por ejemplo, si \( f_x(x, y) = 2x \), consideramos: \[ \lim_{(x,y) \to (1,2)} 2x = 2 \cdot 1 = 2 \] lo que coincide con el valor en el punto: \[ f_x(1,2) = 2 \cdot 1 = 2 \] En el plano -o en dimensiones superiores- un límite existe solo si converge al mismo valor por todos los caminos de aproximación. Verificarlo directamente es prácticamente inviable; por eso se recurre al método de las coordenadas polares trasladadas, que ofrece un enfoque más sistemático y riguroso para analizar el comportamiento de la función desde todas las direcciones. Para estudiar el entorno de \( (1, 2) \), trasladamos el origen mediante el siguiente cambio de coordenadas: \[ x = 1 + r \cos\theta,\quad y = 2 + r \sin\theta \] Sustituyendo en la derivada parcial: \[ f_x(x, y) = 2x = 2(1 + r \cos\theta) = 2 + 2r \cos\theta \] Tomando el límite cuando \( r \to 0 \): \[ \lim_{r \to 0} f_x(x, y) = \lim_{r \to 0} \left(2 + 2r \cos\theta\right) = 2 \] Este límite es independiente de \( \theta \), es decir, no depende de la dirección de aproximación, y coincide con el valor de la derivada en el punto: \[ f_x(1, 2) = 2 \cdot 1 = 2 \] Por tanto, el límite existe, no depende de la trayectoria y coincide con el valor de la derivada en el punto. Concluimos así que \( f_x(x, y) = 2x \) es continua en \( (1, 2) \). El mismo razonamiento debe aplicarse a la otra derivada parcial \( f_y(x,y) \).

Teorema de diferenciabilidad

En síntesis, si una función es diferenciable en un punto, necesariamente es continua en él, posee todas sus derivadas parciales y sus derivadas direccionales se obtienen mediante el producto escalar con el gradiente.

Sin embargo, el recíproco no es cierto: la implicación es solo unidireccional.

Existen funciones que, aun admitiendo todas las derivadas parciales en un punto \( \vec{x}_0 \), no son continuas allí y, por tanto, tampoco diferenciables.

Ejemplo 1

Consideremos la función de dos variables:

\[ f(x, y) = \begin{cases} \displaystyle \frac{xy}{x^2 + y^2} & \text{si } (x, y) \neq (0, 0) \\[6pt] 0 & \text{si } (x, y) = (0, 0) \end{cases} \]

Las derivadas parciales en un punto genérico \((x, y)\) son:

\[ \frac{\partial f}{\partial x}(x, y) = \frac{y(-x^2 + y^2)}{(x^2 + y^2)^2}, \qquad \frac{\partial f}{\partial y}(x, y) = \frac{x(x^2 - y^2)}{(x^2 + y^2)^2} \]

En el origen, ambas derivadas parciales existen y valen 0.

No obstante, si analizamos la continuidad observamos que: a lo largo del eje \( y = 0 \), \( f(x,0) = 0 \); mientras que a lo largo de la recta \( y = x \), \( f(x,x) = \tfrac{1}{2} \). Como los límites difieren, \( f \) no es continua en el origen y, en consecuencia, no es diferenciable allí.

Este ejemplo clásico muestra que disponer de derivadas parciales en un punto no garantiza ni la continuidad ni la diferenciabilidad.

Ejemplo 2

Consideremos ahora:

\[ f(x,y) = \begin{cases} \left( \frac{x^2 y}{x^4 + y^2} \right)^2 & \text{si } (x,y) \neq (0,0) \\[6pt] 0 & \text{si } (x,y) = (0,0) \end{cases} \]

Si nos aproximamos al origen por la parábola \( y = x^2 \), obtenemos \( f(t,t^2) = \tfrac{1}{4} \), mientras que \( f(0,0) = 0 \). El límite depende de la trayectoria y, por tanto, la función no es continua en ese punto.

En cuanto a las derivadas direccionales en el origen, para un vector \( \vec{v} = (\alpha,\beta) \) se tiene:

\[ D_{\vec v} f(0,0) = \lim_{t \to 0} \frac{f(t\alpha,t\beta)}{t} = \lim_{t \to 0} \frac{t \,\alpha^4 \beta^2}{(t^2 \alpha^4 + \beta^2)^2} = 0 \]

Así, todas las derivadas direccionales en el origen existen y son nulas. Sin embargo, la falta de continuidad impide que la función sea diferenciable.

Este ejemplo refuerza la idea de que la existencia de todas las derivadas direccionales -incluso cuando son cero- no basta para garantizar la diferenciabilidad.