Entorno circular

En el espacio vectorial $\mathbb{R^2} = \mathbb{R} \times \mathbb{R}$, un entorno circular (o disco abierto) es el conjunto de puntos interiores de un círculo con centro en $(x_0, y_0)$ y radio positivo $\delta > 0$. $$ I_{\delta} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - x_0)^2 + (y - y_0)^2} < \delta \} $$

El conjunto $I_{\delta}$ constituye un subconjunto de $\mathbb{R^2}$.

Se denomina entorno "abierto" porque excluye los puntos situados en la circunferencia de radio $\delta$ centrada en $(x_0, y_0)$, incluyendo únicamente los puntos estrictamente interiores.

Todos los puntos $(x, y)$ que satisfacen $\sqrt{(x - x_0)^2 + (y - y_0)^2} < \delta$ forman parte del entorno circular $I_{\delta}$; se llaman "puntos interiores" y constituyen el "interior" de $I_{\delta}$. Por ejemplo, el punto A.

En cambio, los puntos que no pertenecen a $I_{\delta}$ se encuentran fuera del círculo abierto y se denominan "puntos exteriores". Por ejemplo, el punto B.

Estos puntos forman parte del complemento del entorno, que se denota $\overline{I}_{\delta} = \mathbb{R^2} - I_{\delta}$.

Los puntos $(x, y)$ situados exactamente en la circunferencia de radio $\delta$, es decir, aquellos para los que $\sqrt{(x - x_0)^2 + (y - y_0)^2} = \delta$, se llaman "puntos frontera". Estos no pertenecen al entorno abierto $I_{\delta}$ y constituyen la frontera del entorno. Por ejemplo, el punto C.

Nota. Si el entorno circular es "abierto", no incluye los puntos frontera. Por ejemplo, el entorno abierto centrado en (0,0) con radio $ \delta = 1 $ es $$ I_{1 \ open} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} < 1 \} $$ En este caso, el entorno contiene todos los puntos cuya distancia al centro es menor que $ \delta = 1 $.

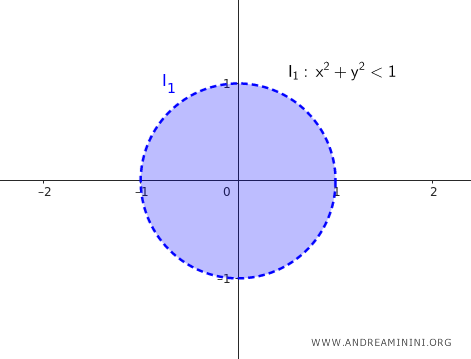
Si el entorno circular es "cerrado", también incorpora los puntos frontera: $$ I_{1 \ closed} = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} \le 1 \} $$ Aquí la condición es "menor o igual" que el radio, de modo que se incluyen los puntos de la circunferencia, es decir, el borde del círculo.

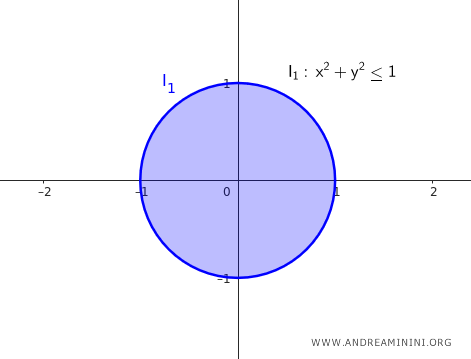
En la topología estándar de $ \mathbb{R^2} $, los entornos se consideran siempre conjuntos abiertos, es decir, sin puntos frontera. Los conjuntos cerrados, por su parte, son los complementos de los abiertos y se expresan como $ C = \mathbb{R^2} - A $. Además, existen conjuntos que son simultáneamente abiertos y cerrados, llamados "clopen". Por ejemplo, el conjunto vacío $ \emptyset $ y todo el espacio $ \mathbb{R^2} $ son abiertos en cualquier topología; como uno es el complemento del otro, también son cerrados. Así, tanto $ \emptyset $ como $ \mathbb{R^2} $ son a la vez abiertos y cerrados. Estos conceptos, sin embargo, pueden resultar abstractos para quienes se inician en la topología, por lo que conviene estudiarlos con detenimiento.

Todos los puntos $ (x,y) $ que, para cualquier radio $ \delta > 0 $, tienen un entorno circular que contiene al menos otro punto de $ I_{\delta} $ distinto de $(x, y)$ se llaman "puntos de acumulación" de $ I_{\delta} $.

En consecuencia, tanto los puntos interiores como los puntos frontera de $ I_{\delta} $ son puntos de acumulación. Así, el punto A y el punto C lo son, mientras que el punto exterior B no lo es.

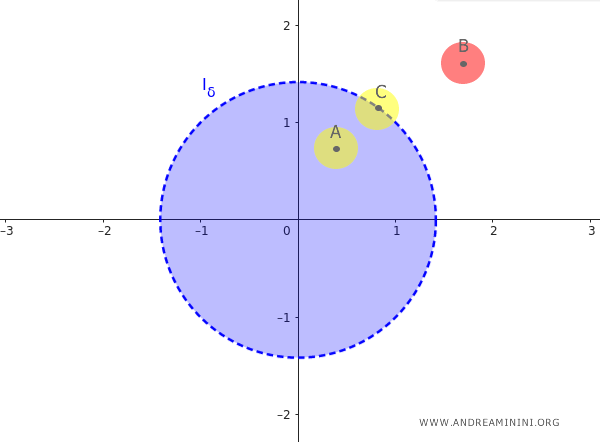
Conviene subrayar que un punto de acumulación no tiene por qué pertenecer al conjunto. Por ejemplo, el punto frontera C no es un elemento de $ I_{\delta} $, pero sí un punto de acumulación de $ I_{\delta} $.

Además, para que un punto $(x;y)$ sea de acumulación, todo entorno suyo, con cualquier radio $ \delta > 0 $, debe contener al menos un punto de $ I_{\delta} $ distinto de $(x;y)$.

Por ejemplo, el punto exterior D tiene un entorno circular suficientemente grande (en amarillo) que incluye algún punto de $ I_{\delta} $, pero no ocurre lo mismo para todo radio. Existen entornos más pequeños (en rojo) que no contienen puntos de $ I_{\delta} $, de modo que D no es un punto de acumulación.

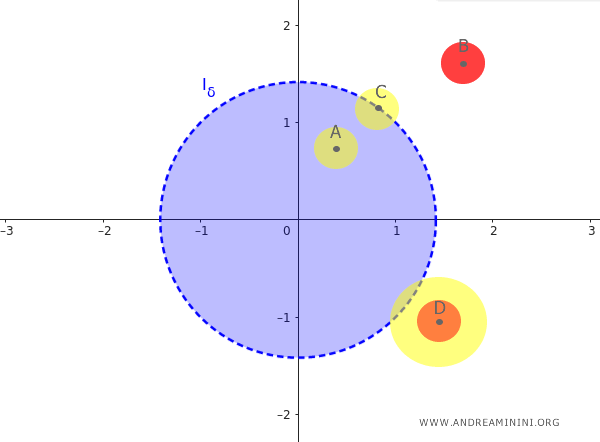
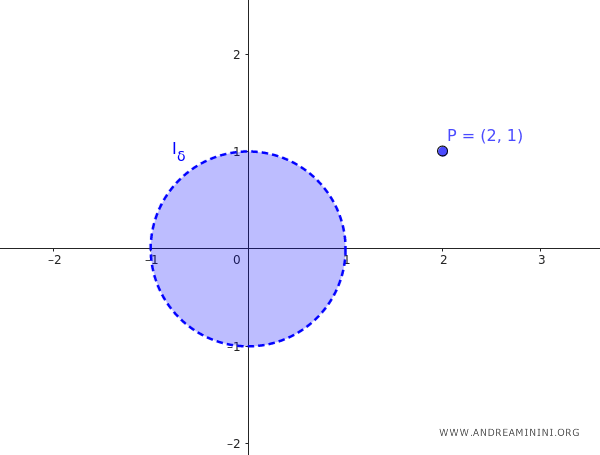
Nota. Si un punto de $ I_{\delta} $ no es de acumulación, se denomina "punto aislado". Por ejemplo, sea $ A $ el conjunto formado por un entorno circular centrado en (0,0) de radio $ \delta = 1 $ y el punto P(2;1): $$ A = \{ (x, y) \in \mathbb{R^2} : \sqrt{(x - 0)^2 + (y - 0)^2} < 1 \} \cup \{ P(2;1) \} $$ El punto P(2;1) es un punto aislado de A porque pertenece a A pero no es un punto de acumulación.

La unión de los puntos de $ I_{\delta} $ con los puntos de acumulación de $ I_{\delta} $ se denomina "clausura" de $ I_{\delta} $, y se denota $ \overline{I}_{\delta} $ o $ \text{Cl}(I_{\delta}) $.

Dicho de otro modo, la clausura de $ I_{\delta} $ es el conjunto formado por los puntos del entorno junto con su frontera.

La clausura de $ I_{\delta} $ es un conjunto cerrado.

Nota. La clausura de $ I_{\delta} $ también puede definirse como la intersección de todos los conjuntos cerrados que contienen a $ I_{\delta} $.

Si un entorno A es un conjunto abierto, su clausura en $ \mathbb{R^2} $ se denomina también dominio de $ \mathbb{R^2} $.

Y así sucesivamente.