Conjuntos abiertos en topología

Un conjunto A se denomina abierto si, para cada elemento x dentro del conjunto (x∈A), existe un vecindario que aún pertenece al conjunto.

 

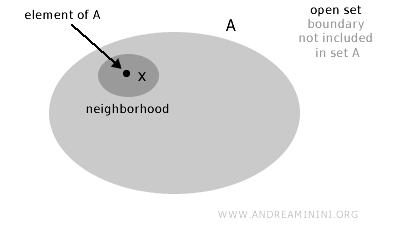
En otras palabras, se considera que un conjunto es abierto si, intuitivamente, sus "fronteras" no forman parte del conjunto mismo.

Más formalmente, un conjunto A en un espacio topológico X es abierto si, para cada punto x en A, existe un vecindario de x que está completamente contenido dentro de A.

Nota. Esto significa que alrededor de cada punto en el conjunto, puedes encontrar una "región" que está totalmente encerrada dentro del conjunto, sin "tocar" el límite externo del conjunto.

Un ejemplo práctico

Un ejemplo sencillo de un conjunto abierto en una línea es un intervalo abierto.

¿Qué es un intervalo abierto? Un intervalo abierto en R es el conjunto de todos los números reales x que satisfacen a < x < b, donde a y b son números reales con a < b.

Este intervalo se denota como (a,b), donde los paréntesis indican que los extremos a y b no están incluidos en el conjunto.

Por ejemplo, el intervalo abierto (3,10) es un conjunto abierto en la línea real.

En este caso, el conjunto A consta de números infinitos entre 3 y 10, excluidos.

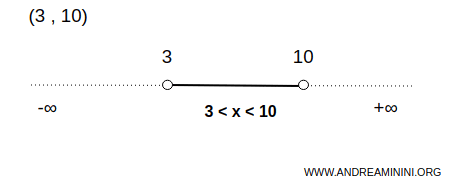
Esto significa que para cada punto x dentro de este intervalo, siempre hay un pequeño intervalo abierto alrededor de x que está completamente contenido dentro de (3,10).

Por ejemplo, para el punto x=3.1, puedo tomar el intervalo abierto (3.09,3.11) que está totalmente contenido en (3,10).

Lo mismo aplica para cualquier otro elemento dentro del intervalo (3,10), porque entre cualquier dos números reales, existen infinitos números reales.

Nota. Incluso si considero un número real muy pequeño dentro del intervalo (3,10), por ejemplo 3.001, todavía puedo construir un vecindario 3.001±0.00000001 que incluye infinitos números reales dentro del intervalo abierto (3,10).

Es un ejemplo sencillo unidimensional de un conjunto abierto.

Otros ejemplos

El mismo concepto se puede extender al espacio bidimensional, como el plano.

Por ejemplo, el conjunto de puntos de un círculo con radio r=1 y centro en el origen (0;0).

$$ x^2+y^2<1 $$

Esta desigualdad describe el conjunto de todos los puntos cuya distancia desde el centro (0,0) es menor que 1, por lo tanto, NO incluyendo los puntos en la circunferencia sino solo aquellos dentro del círculo.

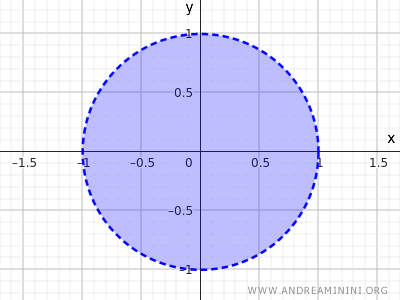
Es otro ejemplo de un conjunto abierto.

¿Cuándo es un conjunto cerrado?

Para tener un conjunto cerrado, simplemente incluye los puntos en la circunferencia en el conjunto.

$$ x^2+y^2 \le 1 $$

En este caso, la condición de que cada elemento del conjunto tenga un vecindario contenido dentro del conjunto ya no se aplica.

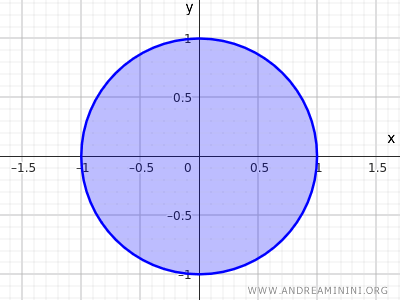
En el caso de un conjunto cerrado, los puntos en la circunferencia no tienen un vecindario completamente contenido dentro del conjunto.

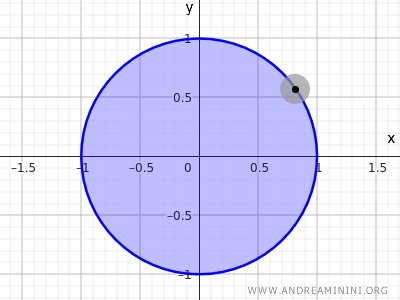
Nota. En topología, la ecuación que define un círculo $ x^2 +y^2=1 $ no es ni un conjunto abierto ni cerrado en el espacio euclidiano R² porque solo considera los puntos en la circunferencia, sin los puntos dentro. Por el contrario, el conjunto de puntos definido por la desigualdad $ x^2+y^2<1 $, que incluye los puntos internos pero no los de la circunferencia, es un ejemplo de un conjunto abierto. Incluir también los puntos de la circunferencia $ x^2+y^2\le 1 $ resultaría en un conjunto cerrado.

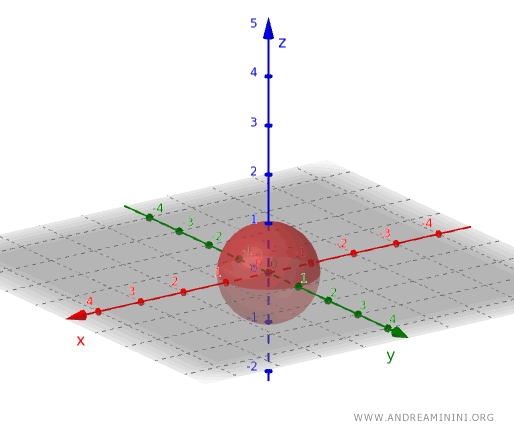
Aplicando el mismo principio, se puede crear un conjunto abierto en el espacio tridimensional considerando, por ejemplo, el conjunto de puntos ubicados dentro de una esfera, excluyendo sin embargo aquellos que yacen en su superficie.

Elegir una topología

Los intervalos abiertos son muy útiles porque son intuitivos y dan una idea inmediata de lo que es un conjunto abierto.

Sin embargo, el concepto de conjunto abierto es mucho más abstracto y no debe limitarse solo a los intervalos abiertos.

Por lo tanto, una vez entendido el concepto, es apropiado profundizar más en él.

El concepto de conjunto "abierto" depende de la topología elegida para aplicar a un espacio.

La idea clave a comprender es que la definición de conjuntos abiertos puede variar drásticamente dependiendo de la topología aplicada a un espacio.

En otras palabras, cualquier conjunto puede considerarse abierto dependiendo de la topología definida para un espacio.

¿Qué es una topología? Una topología en un espacio es esencialmente una colección de conjuntos considerados "abiertos" según ciertas reglas que estos conjuntos deben satisfacer, como la unión arbitraria de conjuntos abiertos siendo aún un conjunto abierto y la intersección de un número finito de conjuntos abiertos siendo aún un conjunto abierto.

Por esta razón, es aconsejable no limitar el pensamiento a los ejemplos más comunes e intuitivos de conjuntos abiertos, como los intervalos abiertos o los discos abiertos.

En topología, la definición de "conjunto abierto" es mucho más amplia y puede incluir conjuntos que, a primera vista, podrían no parecerlo.

Un ejemplo práctico

Considere el espacio \( \{a, b\} \) que contiene solo dos elementos.

En este espacio, se pueden definir al menos dos topologías diferentes: la topología trivial y la topología discreta.

• Topología trivial
  En la topología trivial sobre \( \{a, b\} \), los únicos conjuntos abiertos son el conjunto vacío \( \emptyset \) y el espacio mismo \( \{a, b\} \). Esta es la topología más simple posible, con prácticamente ninguna "estructura abierta" más allá del espacio total y el conjunto vacío.
• Topología discreta
  En la topología discreta, cada posible subconjunto de \( \{a, b\} \) se considera abierto. Esto significa que \( \{ a\} \), \( \{b\} \), \( \{a, b\} \), y \( \emptyset \) son todos conjuntos abiertos. La topología discreta es la más "rica" en términos de conjuntos abiertos, ya que cada combinación de puntos forma un conjunto abierto.

Ahora considerando el conjunto \( \{a\} \) en ambas topologías:

• En la topología trivial, el conjunto {a} no es abierto
  El único conjunto abierto que contiene elementos es \( \{a, b\} \), además del conjunto vacío.
• En la topología discreta, el conjunto {a} es abierto
  En esta topología, cada subconjunto de \( \{a, b\} \), incluyendo \( \{a\} \) y \( \{b\} \), son conjuntos abiertos por definición.

Por lo tanto, el conjunto \( \{a\} \) es un conjunto abierto bajo la topología discreta, pero no bajo la trivial.

Este ejemplo simple destaca cómo la definición de un conjunto abierto está estrechamente ligada a la topología elegida.

Teorema del conjunto abierto

Teorema 1

Dado un conjunto abierto X y una topología T que juntos forman un espacio topológico (X,T), un subconjunto S⊂X es un conjunto abierto en el espacio topológico (X,T) si cada elemento (o punto) s∈S tiene un vecindario U que está completamente contenido dentro del subconjunto S, lo que significa U⊂S.

Por definición, S es un conjunto abierto porque es parte del espacio topológico (X,T).

Por lo tanto, el subconjunto S puede verse como el vecindario de cada uno de sus elementos (puntos) s∈S.

De esto, infiero que el vecindario U_s de cada elemento s∈S es, a su vez, un conjunto abierto contenido dentro de S.

$$ x \in U_s ⊂ S ⊂ X $$

Un conjunto abierto se puede ver como la unión de vecindarios abiertos de sus puntos.

Así, si observo que cada elemento (punto) s∈S de un subconjunto S tiene un vecindario U_s⊂S contenido dentro de S, puedo concluir que el conjunto S es un conjunto abierto porque es la unión de conjuntos abiertos.

En otras palabras, un conjunto es abierto si y solo si, para cada punto dentro del conjunto, existe un vecindario de ese punto que está completamente contenido dentro del conjunto.

Ejemplo. Imagina una mesa esparcida con canicas de vidrio. Cada canica representa un punto dentro de cierto conjunto. Decir que este conjunto es "abierto" es similar a decir que hay suficiente espacio alrededor de cada canica para moverse libremente sin cruzar el borde de la mesa. Si para cada canica en esta mesa, puedo dibujar un círculo alrededor de ella, completamente contenido en la mesa (sin tocar los bordes), entonces el conjunto de canicas en la mesa representa un "conjunto abierto". Esencialmente, la apertura del conjunto significa que no importa qué canica elija, siempre hay algún "espacio libre" alrededor de ella que todavía pertenece al conjunto de canicas en la mesa.

Teorema 2

Toma un conjunto \( X \) y una base \( B \) para una topología en \( X \). Un subconjunto \( A \subset X \) califica como un conjunto abierto en la topología generada por \( B \) si y solo si, para cada elemento \( x \) en \( A \), hay un elemento base \( B _x \) en \( B \) tal que \( x \) está dentro de \( B_x \) y \( B_x \) está completamente contenido en \( A \), lo que significa \( B_x \subseteq A \).

Este teorema resalta una característica clave de las topologías formadas por una base.

En pocas palabras, cada punto en un conjunto abierto \( A \) debe tener un "vecindario" a su alrededor, \( B_x \), que pertenece a los conjuntos base y está completamente encerrado por \( A \).

Esto confirma que el conjunto \( A \) es de hecho abierto en la topología creada por \( B \).

Prueba. Si A es un conjunto abierto en la topología generada por la base B en el conjunto X, donde A es un subconjunto de X, entonces por definición, A es la unión de los elementos base. En consecuencia, cada elemento x en A pertenece a al menos un elemento base Bx, y este Bx está completamente contenido dentro del conjunto A, lo que significa B_x es un subconjunto de A, ya que A es la unión de los elementos base. Este razonamiento se puede invertir. Si cada elemento x en A está contenido dentro de al menos un elemento base B_x que está completamente contenido dentro de A, o en otras palabras, B_x es un subconjunto de A, entonces el conjunto A es abierto en la topología generada por B.

Ejemplo

Considerando el conjunto \( X = \{1, 2, 3, 4, 5\} \) y una base para una topología en \( X \) como \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \), determinemos si el conjunto \( A = \{1, 2, 3\} \) es abierto.

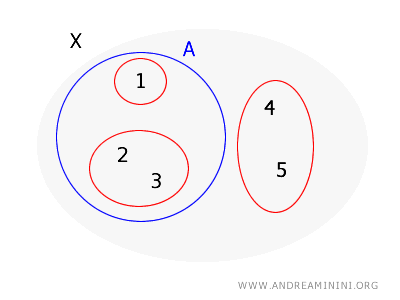
Para cada punto en \( A \), necesito encontrar un conjunto base que lo contenga y esté completamente dentro de \( A \):

• Para el punto \( 1 \) en \( A \), está el conjunto base \( \{1\} \) que contiene \( 1 \) y está completamente contenido en \( A \).
• Para el punto \( 2 \) en \( A \), el conjunto base \( \{2, 3\} \) contiene \( 2 \) y está completamente contenido en \( A \).
• Para el punto \( 3 \) en \( A \), el mismo conjunto base \( \{2, 3\} \) contiene \( 3 \) y está completamente dentro de \( A \).

Cada punto en \( A \) está incluido en un conjunto base que, a su vez, está contenido en \( A \), cumpliendo con la condición del teorema.

Por lo tanto, puedo concluir que \( A \) es un conjunto abierto en la topología generada por la base \( B \).

Ejemplo 2

Considerando el mismo conjunto \( X = \{1, 2, 3, 4, 5\} \) y base para una topología en \( X \) definida como \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) del ejemplo anterior.

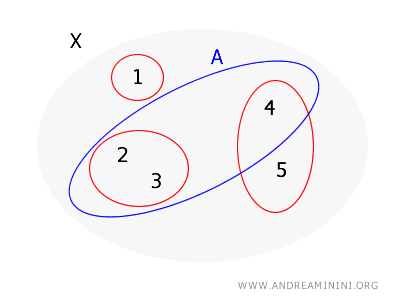
Esta vez, sin embargo, quiero verificar si el conjunto \( A = \{2, 3, 4\} \) es abierto.

• Para el punto \( 2 \), puedo usar el conjunto base \( \{2, 3\} \), que está completamente dentro de \( A \).
• Para el punto \( 3 \), está el mismo conjunto base \( \{2, 3\} \) cubriéndolo y completamente dentro de \( A \).
• Para el punto \( 4 \), no hay un conjunto base que lo contenga y que también esté completamente dentro de \( A \) porque el único conjunto base que incluye 4 es \( \{4, 5\} \), que no está completamente dentro de \( A \) (ya que incluye 5, que no está en \( A \)).

Por lo tanto, según el teorema, el conjunto \( A \) no es un conjunto abierto en la topología generada por la base \( B \), porque no todos los puntos en \( A \) tienen un conjunto base que esté completamente contenido dentro de \( A \).

Notas complementarias

Algunas observaciones y consideraciones sobre los conjuntos abiertos

• Un conjunto A es abierto si y solo si A = Int(A)
  Un conjunto \( A \) en un espacio topológico \( X \) es abierto precisamente cuando coincide con su interior. El interior de un conjunto, denotado Int(A), se define como la unión de todos los conjuntos abiertos contenidos en \( A \). $$ A = \text{Int}(A) $$

Y así en adelante.