Espacio de Hausdorff
Un espacio de Hausdorff es un tipo de espacio topológico en el que cualesquiera dos puntos distintos pueden separarse mediante entornos abiertos disjuntos. Esta propiedad garantiza que cada punto pueda distinguirse de los demás de manera inequívoca.
En términos más intuitivos, en un espacio de Hausdorff siempre es posible encontrar entornos abiertos \( U \) y \( V \) para cualesquiera dos puntos \( x \) y \( y \), de modo que estos entornos no se superpongan, es decir, que \( U \cap V = \emptyset \).
Esta característica proporciona una noción formal de separabilidad que refleja nuestra intuición sobre la distancia y la proximidad en la geometría euclidiana.
Los espacios de Hausdorff juegan un papel fundamental en análisis y geometría, ya que permiten manejar con facilidad la convergencia de sucesiones y otras construcciones topológicas esenciales.
Un hecho notable es que en cualquier espacio de Hausdorff, los conjuntos formados por un único punto son conjuntos cerrados.
En efecto, el complemento de cualquier punto individual - es decir, el conjunto de todos los demás puntos - siempre es un conjunto abierto.
Ejemplos prácticos
Ejemplo 1
Consideremos la topología estándar, que se usa habitualmente para definir la estructura topológica de la recta real \(\mathbb{R}\).

En esta topología, los puntos individuales no son conjuntos abiertos.
Explicación: En la topología estándar, un conjunto abierto debe contener, junto con cada uno de sus puntos, un intervalo abierto completo a su alrededor. Dado que entre dos números reales siempre hay infinitos valores intermedios, un conjunto reducido a un único punto \( \{x\} \) no puede cumplir esta condición. Carece del "margen" necesario para formar parte de un conjunto abierto sin incluir otros puntos cercanos. Como consecuencia, los puntos individuales no son abiertos en la topología usual de \(\mathbb{R}\).
Sin embargo, el complemento de cada punto \( \mathbb{R} \setminus \{x\} \) sí es un conjunto abierto.

Esto implica que cualquier punto \( \{x\} \) es un conjunto cerrado, ya que su complemento es abierto.
Además, la topología estándar de \(\mathbb{R}\) es un espacio de Hausdorff, porque para cualquier par de puntos distintos \( a \) y \( b \) es posible encontrar entornos abiertos que los separen.
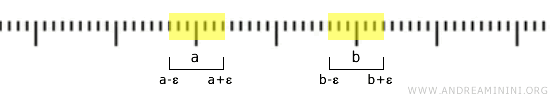
Por ejemplo, si \( a < b \), podemos elegir los intervalos abiertos \( (a-\epsilon, a+\epsilon) \) y \( (b-\epsilon, b+\epsilon) \), con \( \epsilon \) lo suficientemente pequeño para garantizar que \( a+\epsilon < b-\epsilon \), asegurando así que los dos entornos sean disjuntos.
En definitiva, el hecho de que los puntos individuales sean conjuntos cerrados en la topología estándar confirma que \(\mathbb{R}\), con su topología usual, es un espacio de Hausdorff.
Ejemplo 2
Consideremos un espacio topológico definido sobre el conjunto \( X = \{1,2,3\} \), equipado con la topología discreta.
En la topología discreta, cada punto de \( X \) es, por definición, un conjunto abierto.
Esto implica que todos los subconjuntos de \( X \) son abiertos:
- El conjunto vacío \( \emptyset \)
- Los conjuntos unitarios \( \{1\} \), \( \{2\} \), \( \{3\} \)
- Los conjuntos formados por dos elementos \( \{1, 2\} \), \( \{1, 3\} \), \( \{2, 3\} \), obtenidos como uniones o intersecciones de conjuntos abiertos
- El conjunto total \( \{1, 2, 3\} \)
En total, hay \( 2^3 = 8 \) conjuntos abiertos, correspondientes a todos los subconjuntos de \( X \).
Bajo esta topología, el espacio es siempre un espacio de Hausdorff.
Por definición, un espacio es de Hausdorff si, para cada par de puntos distintos \( x \) e \( y \), existen entornos abiertos \( U \) y \( V \) tales que \( U \cap V = \emptyset \) y \( x \in U \), \( y \in V \).
En la topología discreta, dado que cada punto forma un conjunto abierto por sí mismo, para cualquier par de puntos distintos \( x \) e \( y \) en \( X = \{1,2,3\} \), podemos tomar simplemente \( U = \{x\} \) y \( V = \{y\} \).
Dado que estos conjuntos son disjuntos (\( U \cap V = \emptyset \)), se cumple la condición de Hausdorff.
Por ejemplo, si elegimos \( x = \{1\} \) e \( y = \{2\} \), con \( U = \{1\} \) y \( V = \{2\} \), su intersección es el conjunto vacío:
$$ \{1\} \cap \{2\} = \emptyset $$
Esto ilustra que los puntos en la topología discreta siempre tienen entornos abiertos que los separan.
Lo mismo ocurre para cualquier otro par de puntos en \( X \).
En la topología discreta, ¿los puntos individuales son abiertos o cerrados?
Cuando me encontré con esta cuestión por primera vez, me resultó desconcertante. Si la topología discreta es un espacio de Hausdorff, entonces los conjuntos unitarios \( \{x\} \) deberían ser cerrados. Pero, por la propia definición de la topología discreta, también son abiertos. ¿Cómo es posible?
La respuesta es sorprendentemente sencilla, aunque inicialmente pueda parecer contraintuitiva: en topología, un conjunto puede ser simultáneamente abierto y cerrado. Este tipo de conjuntos se denominan conjuntos clopen. En este contexto, "cerrado" no es necesariamente el opuesto de "abierto".
En la topología discreta, cada conjunto unitario \( \{x\} \) es cerrado porque su complemento, formado por todos los demás puntos del espacio, es abierto, ya que cualquier subconjunto es un conjunto abierto en esta topología.
Por lo tanto, si el complemento de un conjunto \( \{x\} \) es abierto, se sigue que \( \{x\} \) también es un conjunto cerrado.
Por ejemplo, si tomamos \( X = \{1,2,3\} \) y consideramos el punto \( \{1\} \), este es un conjunto abierto por la definición de la topología discreta. Sin embargo, también es cerrado, porque su complemento, \( X \setminus \{1\} = \{2,3\} \), es un conjunto abierto. En topología, el complemento de un conjunto abierto es un conjunto cerrado.
En resumen, los puntos individuales \( \{x\} \) en la topología discreta son simultáneamente abiertos y cerrados, ya que todos los subconjuntos son abiertos por definición, y sus complementos también lo son, lo que implica que los conjuntos unitarios son cerrados.
- Abierto
En la topología discreta, cada punto es un conjunto abierto por definición. - Cerrado
El complemento \( X \setminus \{x\} \), que contiene todos los demás elementos del espacio, es un conjunto abierto. Dado que los complementos de los puntos son abiertos, los puntos mismos son conjuntos cerrados.
En definitiva, los puntos individuales \( \{x\} \) son abiertos porque todos los subconjuntos son abiertos en la topología discreta, y son cerrados porque sus complementos también son abiertos.
Una diferencia clave entre la topología discreta y la estándar es que, en la topología estándar, no todos los subconjuntos son abiertos. Solo aquellos que cumplen la definición de "entorno abierto" para cada uno de sus puntos se consideran abiertos.
Observaciones
Algunas propiedades y consecuencias importantes de los espacios de Hausdorff:
- En un espacio de Hausdorff, toda sucesión convergente tiene un único límite
En un espacio de Hausdorff \( X \), cualquier sucesión de puntos que converge lo hace a un único punto \( x \in X \). Si una sucesión pudiera converger a dos puntos distintos, estos tendrían entornos abiertos solapados, lo cual contradice la definición de espacio de Hausdorff.
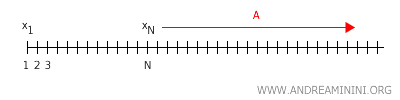
Demostración: Sea \( X \) un espacio de Hausdorff (por ejemplo, la recta real \( X = \mathbb{R} \)). Supongamos, por contradicción, que existe una sucesión de puntos \( x_1, x_2, x_3, \dots \) que converge a dos puntos distintos \( x \) e \( y \) en \( X \). Según la definición de convergencia en un espacio topológico, esto implica que existe un entero \( N \) tal que, para todo \( n > N \), los puntos \( x_n \) se encuentran dentro de un entorno \( A \) de \( x \).
Simultáneamente, existe un entero \( M \) tal que, para todo \( n > M \), los puntos \( x_n \) se encuentran en un entorno \( B \) de \( y \).
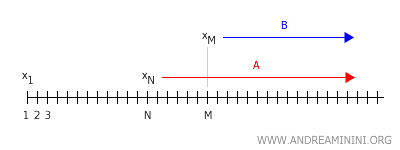
Si \( M > N \), algunos puntos en \( A \) también estarían en \( B \), lo que implica que \( A \cap B \neq \emptyset \), en contradicción con la propiedad de Hausdorff. Por lo tanto, en un espacio de Hausdorff, una sucesión no puede converger a más de un punto.