Frontera de un conjunto
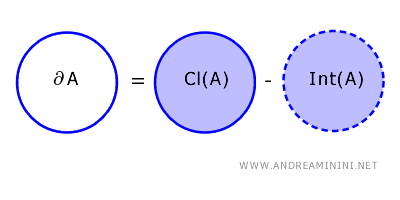
La frontera de un subconjunto \( A \) en un espacio topológico \( X \) es el conjunto de puntos que pertenecen al cierre de \( A \), pero no a su interior: \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]
Aquí, \( \text{Cl}(A) \) representa el cierre de \( A \), que incluye tanto los puntos de \( A \) como sus puntos límite.
Por su parte, \( \text{Int}(A) \) es el interior de \( A \), es decir, el conjunto de puntos de \( A \) que poseen un entorno contenido por completo en \( A \).
Conviene subrayar que el concepto de frontera no es una propiedad intrínseca del conjunto, sino que depende de la topología con la que se trabaje.
En consecuencia, la frontera de un conjunto puede cambiar si se considera una topología distinta.
Dicho de otro modo, la frontera de un conjunto \( A \) está formada por los puntos que están “cerca” tanto de \( A \) como de su complemento \( X \setminus A \).
Un ejemplo práctico
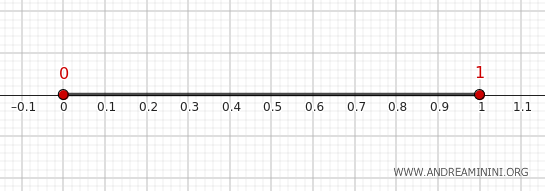
Consideremos el conjunto \( A = (0, 1) \), visto como subconjunto de la recta real \( \mathbb{R} \) con su topología usual.
Vamos a determinar su frontera paso a paso.
1] Cálculo del cierre de A
El cierre de \( A \), denotado \( \text{Cl}(A) \), incluye todos los puntos del conjunto y sus puntos límite.
En el caso de \( A = (0, 1) \), el cierre es el intervalo cerrado \([0, 1]\), ya que los extremos 0 y 1 son puntos límite de \( A \), y todos los puntos intermedios también lo son.
$$ \text{Cl}(A) = [0, 1] $$
2] Cálculo del interior de A
El interior de \( A \), denotado \( \text{Int}(A) \), está constituido por todos los puntos que admiten un entorno completamente contenido en \( A \).
Como \( A = (0, 1) \) es un intervalo abierto, su interior coincide con él mismo:
$$ \text{Int}(A) = (0, 1) $$
3] Cálculo de la frontera de A
La frontera de \( A \), es decir, \( \partial A \), se obtiene restando al cierre de \( A \) su interior:
$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$
Aplicando los resultados anteriores:
$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$
Por tanto, bajo la topología usual en \( \mathbb{R} \), la frontera del conjunto \( A = (0,1) \) está formada por los puntos \(\{0, 1\}\).
Ambos puntos están "en el borde" del conjunto, ya que todo entorno suyo contiene tanto puntos de \( A \) como de su complemento.
Teorema de la frontera
Un punto \( x \in X \) pertenece a la frontera \( \partial A \) de un subconjunto \( A \) si, y solo si, todo entorno de \( x \) intersecta tanto \( A \) como su complemento \( X - A \).
Este teorema proporciona un criterio práctico: para saber si un punto \( x \) está en la frontera de \( A \), basta comprobar que cualquier entorno suyo corta simultáneamente a \( A \) y a \( X - A \).
Ejemplo
Consideremos de nuevo \( A = (0, 1) \) en \( \mathbb{R} \), con la topología estándar.
Sabemos que:
$$ \text{Cl}(A) = [0, 1] \quad \text{e} \quad \text{Int}(A) = (0, 1) $$
Así que la frontera es:
$$ \partial A = \{0, 1\} $$
Comprobemos que estos puntos cumplen el criterio del teorema.
1] Verificación para el punto 0
Tomemos un entorno de 0, por ejemplo \( (0 - \epsilon, 0 + \epsilon) \) con \( \epsilon > 0 \).
Este entorno intersecta \( A \) porque incluye puntos de \( (0, 1) \), y también intersecta \( X - A \), ya que contiene puntos menores o iguales que 0.
Por lo tanto, \( 0 \in \partial A \).
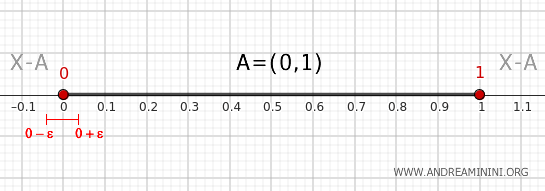
2] Verificación para el punto 1
Consideremos ahora un entorno de 1, por ejemplo \( (1 - \epsilon, 1 + \epsilon) \).
Este entorno también corta \( A \) (contiene puntos de \( (0,1) \)) y corta \( X - A \), al incluir puntos mayores o iguales que 1.
Así, \( 1 \in \partial A \).
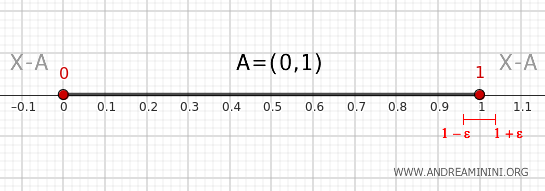
3] Verificación para un punto interior
Elijamos un punto cualquiera dentro del intervalo \( (0,1) \), por ejemplo 0.5.
Todo entorno de 0.5 está completamente contenido en \( A \), por lo que no puede intersectar \( X - A \).
Luego, \( 0.5 \notin \partial A \).
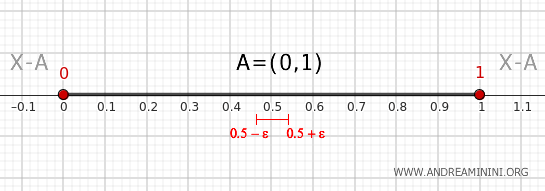
En resumen, el teorema nos confirma que los puntos 0 y 1 pertenecen a la frontera de \( A = (0, 1) \), mientras que un punto como 0.5 no lo está. La frontera es, efectivamente, \(\{0, 1\}\).
Notas
Algunas observaciones importantes sobre las fronteras en topología:
- La frontera \( \partial A \) está contenida en \( A \) si y solo si \( A \) es cerrado:
\[ \partial A \subseteq A \Leftrightarrow A \text{ es cerrado} \] - La frontera \( \partial A \) y el conjunto \( A \) no tienen puntos en común si y solo si \( A \) es abierto:
Es decir, \( A \) es abierto ⇔ ninguno de sus puntos está en la frontera.
\[ \partial A \cap A = \emptyset \Leftrightarrow A \text{ es abierto} \] - La frontera \( \partial A \) es vacía si y solo si \( A \) es abierto y cerrado a la vez (clopen):
\[ \partial A = \emptyset \Leftrightarrow A \text{ es clopen} \] - La frontera \( \partial A \) coincide con la intersección del cierre de \( A \) y el del complemento \( X - A \):
\[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \] - La frontera \( \partial A \) siempre es un conjunto cerrado
La intersección de dos conjuntos cerrados también es cerrada. Dado que \( \partial A \) se define como \(\text{Cl}(A) \cap \text{Cl}(X - A)\), podemos afirmar que \( \partial A \) es siempre cerrado.
- La frontera y el interior de un conjunto no tienen puntos en común:
\[ \partial A \cap \text{Int}(A) = \emptyset \] - La unión del interior con la frontera es igual al cierre del conjunto:
\[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]
Y así sucesivamente.