Transformaciones topológicas

Transformaciones topológicas son operaciones aplicadas a espacios topológicos que conservan propiedades fundamentales como la conectividad y la continuidad.

Estas transformaciones son esenciales en el estudio de la topología, una rama de las matemáticas que se enfoca en propiedades de espacios que se mantienen constantes bajo transformaciones continuas.

Algunas características clave de las transformaciones topológicas incluyen:

• Continuidad
  Una transformación topológica debe ser continua, lo que significa que cambios mínimos en las entradas deberían resultar en cambios mínimos en las salidas.
• Conectividad y Proximidad
  Las transformaciones topológicas preservan nociones de proximidad y conectividad. Si dos puntos están cerca o conectados en el espacio original, lo seguirán estando en el espacio transformado.
• Deformación sin rupturas ni uniones
  Los objetos pueden estirarse, comprimirse o doblarse, pero no pueden ser desgarrados ni unidos. Por ejemplo, un donut puede transformarse en una taza de café a través de una transformación topológica, ya que ambos contienen un solo "agujero".

Aplicaciones: Las transformaciones topológicas se emplean en una amplia gama de campos, desde matemáticas puras como la teoría de nudos y la topología algebraica, hasta la exploración de propiedades de objetos invariantes bajo deformaciones continuas.

Tipos de Transformaciones Topológicas

En topología, se categorizan las transformaciones según su capacidad para preservar propiedades topológicas específicas.

He aquí algunos de los tipos fundamentales de transformaciones topológicas:

• Homeomorfismos
  Un homeomorfismo es una transformación continua que posee un inverso también continuo. Esencialmente, permite transformar un espacio en otro y revertir el proceso sin causar "roturas" o "uniones". Estas transformaciones son fundamentales en topología. Por ejemplo, la transformación de una taza en un donut, como se mencionó previamente.
• Isotopías
  Una isotopía es un caso particular de homeomorfismo donde cada fase de la transformación es también un homeomorfismo. Por ejemplo, mover un nudo a lo largo de una cuerda sin apretar ni aflojarlo, cada movimiento representa una isotopía.
• Homotopías
  Estas transformaciones muestran cómo una función puede "deformarse" en otra mientras se conservan algunas propiedades topológicas. La homotopía es menos restrictiva que el homeomorfismo. Por ejemplo, al estirar un resorte y luego soltarlo, las diferentes formas durante la extensión y liberación son homotópicas.
• Difeomorfismos
  Un difeomorfismo es un homeomorfismo que además es diferenciable. Esto es especialmente relevante en la topología diferencial, donde importa la suavidad y diferenciabilidad de las superficies. Por ejemplo, transformar una esfera estirable en un elipsoide alargado.

Estos tipos de transformación se centran en distintos aspectos de la continuidad y la capacidad de deformación de espacios y funciones en topología.

Su uso varía dependiendo del contexto específico en que se aplican, como en topología general, topología algebraica o topología diferencial.

Diferencias entre Transformaciones Geométricas y Topológicas

Las transformaciones geométricas y topológicas se diferencian en sus propiedades y aplicaciones:

• Transformaciones Geométricas
  Las transformaciones geométricas modifican objetos en el espacio, conservando propiedades geométricas como distancias, ángulos y formas. Ejemplos de estas son las traslaciones, rotaciones, reflexiones y escalados.

  Por ejemplo, una rotación mantiene distancias y ángulos, aunque cambia la orientación.

• Transformaciones Topológicas
  Las transformaciones topológicas modifican espacios preservando propiedades topológicas como la conectividad y la continuidad, pero no necesariamente distancias o ángulos. Estas transformaciones son notablemente flexibles, permitiendo deformar figuras sin cortes ni uniones.

  Por ejemplo, la topología permite que un donut se transforme en una taza de café porque ambos comparten un único agujero.

Mientras que las transformaciones geométricas se centran en movimientos de objetos o cambios de forma preservando medidas y proporciones específicas, las transformaciones topológicas destacan por su capacidad para deformar el espacio preservando la conectividad y la continuidad, independientemente de la forma o tamaño específicos.

¿Pueden las transformaciones ser tanto geométricas como topológicas?

Sí, ciertas transformaciones no solo modifican objetos manteniendo propiedades geométricas como ángulos, longitudes y formas, sino que también son continuas y conservan propiedades topológicas como la conectividad y la continuidad.

Aquí algunos ejemplos prácticos:

• Isometrías
  Las isometrías, como las traslaciones, rotaciones y reflexiones, conservan propiedades como las distancias entre puntos y los ángulos, siendo transformaciones tanto geométricas como topológicas. Son específicamente homeomorfismos porque también cuentan con un inverso continuo.
  
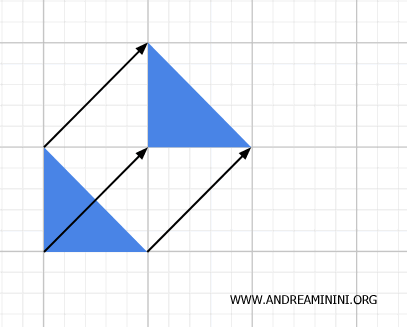
• Similitudes
  Las similitudes cambian el tamaño del objeto pero conservan la forma, incluidas dilataciones o contracciones que mantienen ángulos y proporciones relativas. Estas son transformaciones geométricas por su impacto en la forma y el tamaño, pero también son topológicas porque son continuas y preservan la conectividad.

Estas transformaciones demuestran que las propiedades geométricas y topológicas no siempre son excluyentes. En algunos casos, una transformación puede tener importancia geométrica y ser topológicamente válida al mismo tiempo.

Y así sucesivamente.