Convergencia en un espacio topológico

En un espacio topológico $ X $, un punto $ x \in X $ se dice límite de una sucesión $ (x_n) $ si, para toda vecindad $ U $ de $ x $, existe un entero positivo $ N $ tal que, para todo $ n \geq N $, se cumple que $ x_n \in U $.

Es decir, la sucesión $ (x_n) $ converge a $ x $ si a partir de cierto índice todos sus términos permanecen contenidos en cualquier vecindad de $ x $.

Esta definición se expresa formalmente como:

$$ \lim_{n \to \infty} x_n = x $$

En tal caso, se dice que $ x $ es el límite de la sucesión $ (x_n) $.

Ejemplo ilustrativo

Analicemos un ejemplo concreto con la sucesión $ \left( \frac{1}{n} \right) $ en el espacio topológico $ X = \mathbb{R} $ provisto de la topología usual.

$$ x_n = \left( \frac{1}{n} \right) $$

Queremos demostrar que $ \left( \frac{1}{n} \right) $ converge a 0, es decir, que $ 0 $ es el límite de la sucesión.

Para ello, consideremos una vecindad arbitraria $ U $ de $ 0 $.

En la topología estándar sobre $ \mathbb{R} $, toda vecindad de $ 0 $ contiene un intervalo abierto del tipo $ (-\epsilon, \epsilon) $, con $ \epsilon > 0 $.

Debemos encontrar un entero $ N \in \mathbb{N} $ tal que, para todo $ n \geq N $, se cumpla $ \frac{1}{n} \in (-\epsilon, \epsilon) $.

Dado $ \epsilon > 0 $, basta tomar $$ N = \left\lceil \frac{1}{\epsilon} \right\rceil. $$ Entonces, para todo $ n \geq N $, tenemos:

$$ n \geq \frac{1}{\epsilon} \quad \Rightarrow \quad \frac{1}{n} \leq \epsilon $$

De lo cual se deduce que: $$ \left| \frac{1}{n} \right| < \epsilon \quad \text{para todo } n \geq N. $$

Así, para cualquier vecindad $ U $ de $ 0 $, existe un índice $ N $ tal que todos los términos posteriores de la sucesión se encuentran dentro de $ U $. En consecuencia, $$ \lim_{n \to \infty} \frac{1}{n} = 0 $$

Esto demuestra que $ 0 $ es el límite de la sucesión $ \left( \frac{1}{n} \right) $.

$$ \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$

Dicho de otro modo, la sucesión $ \frac{1}{n} $ converge a cero porque, a partir de cierto índice, todos sus términos permanecen dentro de cualquier entorno de cero.

A continuación se presenta una tabla con los diez primeros términos de la sucesión:

$$ \begin{array}{|c|c|} \hline n & \frac{1}{n} \\ \hline 1 & 1 \\ 2 & 0.5 \\ 3 & 0.333 \\ 4 & 0.25 \\ 5 & 0.2 \\ 6 & 0.167 \\ 7 & 0.143 \\ 8 & 0.125 \\ 9 & 0.111 \\ 10 & 0.1 \\ \hline \end{array} $$

Por ejemplo, si tomamos $ N = 5 $, de modo que $ x_5 = \frac{1}{5} = 0.2 $, entonces para todo $ n > 5 $, los términos posteriores de la sucesión pertenecen a la vecindad $ U = (0, 0.2) $.

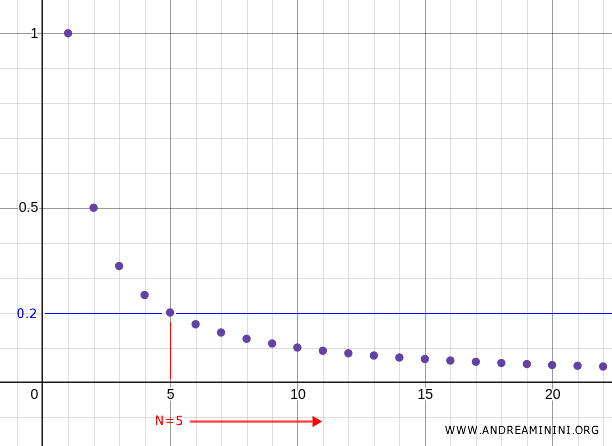
ejemplo de punto de convergencia

Lo mismo sucede para cualquier otro valor de $ N $.

Por ejemplo, si tomamos $ N = 10 $, entonces $ x_{10} = 0.1 $, y para todo $ n > 10 $, los términos de la sucesión se encuentran en la vecindad $ U = (0, 0.1) $, y así sucesivamente.

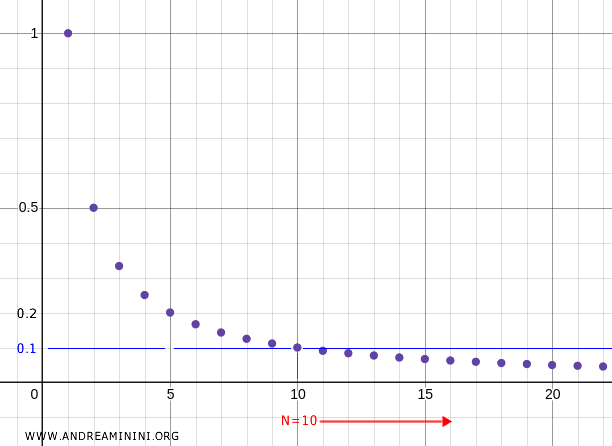
visualización de la sucesión convergente

Concluimos, por tanto, que $ 0 $ es el límite de la sucesión.

Y así sucesivamente.