Topología Discreta
La topología discreta \( T \) es la topología más extensa que se puede definir sobre un conjunto \( X \), ya que contiene todos sus subconjuntos posibles.
En la topología discreta, la familia de conjuntos abiertos \( T \) incluye absolutamente todos los subconjuntos de \( X \). En consecuencia, cualquier subconjunto de \( X \) se considera un conjunto abierto.
Esto implica que cada elemento de \( X \) es un conjunto abierto por sí mismo, lo que a su vez significa que cada punto es "aislado" de los demás.
En otras palabras, no existe ninguna restricción sobre la cercanía entre los elementos; cualquier disposición es admisible.
Nota. Una topología sobre un conjunto \( X \) es una colección de subconjuntos de \( X \) (denominados "abiertos") que satisface tres condiciones fundamentales:
- El conjunto vacío y el conjunto total \( X \) deben pertenecer a la colección \( T \).
- La unión arbitraria de conjuntos de \( T \) también debe pertenecer a \( T \).
- La intersección finita de conjuntos de \( T \) debe formar parte de \( T \).
Se denomina "discreta" porque trata los elementos de \( X \) como entidades completamente separadas, sin ninguna noción de proximidad o continuidad entre ellos.
Es la topología más grande que se puede definir en un conjunto, en el sentido de que ninguna otra topología puede contener más conjuntos abiertos que la discreta, ya que esta ya incluye todos los subconjuntos de \( X \).
Nota. Estas condiciones establecen la base para el estudio de los conjuntos abiertos, permitiendo analizar cómo los elementos de un espacio pueden estar "cercanos" o conectados sin interrupciones, lo que da lugar al concepto de continuidad.
Una propiedad fundamental de esta topología es la siguiente:
En la topología discreta, todo subconjunto de un espacio topológico es simultáneamente abierto y cerrado.
Esta característica se debe a que la topología discreta considera abiertos todos los subconjuntos del espacio.
Por lo tanto, el complemento de cualquier subconjunto de \( X \) también es un conjunto abierto.
En topología, un conjunto se considera cerrado si su complemento es abierto.
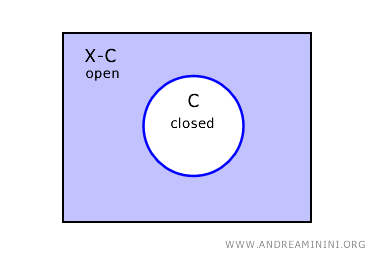
Así pues, si el complemento de cualquier subconjunto es abierto, entonces todos los subconjuntos también son cerrados.
Esta peculiaridad de la topología discreta garantiza que cualquier subconjunto sea "clopen", es decir, al mismo tiempo cerrado y abierto, sin excepciones.
Nota. En la topología discreta, esta propiedad se cumple para cualquier subconjunto, no solo para puntos individuales. Esto ocurre porque cada punto en sí mismo es un conjunto abierto, al igual que cualquier combinación de puntos. Dado que el complemento de cualquier subconjunto es también un subconjunto de \( X \) y, por lo tanto, abierto, se concluye que todo subconjunto es necesariamente cerrado.
Un Ejemplo Práctico
Veamos un ejemplo sencillo de topología discreta considerando un conjunto finito \( X \) con tres elementos.
$$ X = \{a, b, c\} $$
El conjunto potencia de \( X \), es decir, el conjunto de todos los subconjuntos posibles de \( X \), está compuesto por los siguientes elementos:
- El conjunto vacío: \(\emptyset\)
- Subconjuntos unitarios: \(\{a\}\), \(\{b\}\), \(\{c\}\)
- Subconjuntos con dos elementos: \(\{a, b\}\), \(\{a, c\}\), \(\{b, c\}\)
- El conjunto total: \(\{a, b, c\}\)
En la topología discreta sobre \( X \), cada subconjunto de \( X \) se considera un conjunto abierto.
Por lo tanto, la topología discreta \( T \) en \( X \) está dada por:
$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\} \} $$
En esta topología, por definición, todos los subconjuntos de \( X \) son abiertos.
Nota. Esta familia de conjuntos forma una topología porque incluye \( X \) y el conjunto vacío. Además, cualquier unión arbitraria o intersección finita de conjuntos abiertos sigue perteneciendo a \( T \). Dado que en la topología discreta todos los subconjuntos son abiertos, no hay restricciones en cuanto a la noción de proximidad o continuidad entre los elementos de \( X \).
Consideremos el subconjunto \( \{ a \} \). De acuerdo con la definición de la topología discreta, este es un conjunto abierto.
A su vez, el subconjunto \( \{ a \} \) es cerrado, ya que su complemento, \( X \setminus \{a\} = \{b, c\} \), también es un conjunto abierto. Recordemos que un conjunto es cerrado si su complemento es abierto.
Así que, en la topología discreta, el subconjunto \( \{ a \} \) es simultáneamente abierto y cerrado.
Lo mismo ocurre con cualquier otro subconjunto de la topología.
Y así sucesivamente.