Interior de un Conjunto

En un espacio topológico \( X \), el interior de un conjunto \( A \) es la unión de todos los subconjuntos abiertos contenidos en \( A \). Se denota habitualmente como \( \text{Int}(A) \) o \( A^\circ \).

El interior de un conjunto es el conjunto abierto más grande que está completamente contenido dentro de \( A \).

No existe ningún subconjunto abierto de \( A \) que sea más grande que su interior.

Nota: El interior de un conjunto es, por definición, una unión de conjuntos abiertos, por lo que siempre es un conjunto abierto.

Formalmente, el interior de \( A \) es el conjunto de todos los puntos de \( A \) que tienen un entorno abierto completamente contenido en \( A \).

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ es abierto en } X \} $$

En otras palabras, un punto \( x \) pertenece al interior de \( A \) si existe un conjunto abierto \( U \) tal que \( x \in U \) y \( U \subseteq A \).

Es importante recordar que el interior de un conjunto \( A \) depende de la estructura topológica \( X \) en la que está contenido, y no solo de \( A \) en sí mismo. Por lo tanto, el interior de \( A \) puede variar dependiendo de la topología de \( X \).

Ejemplo Práctico

Consideremos el conjunto \( A = [0,1] \) en \( \mathbb{R} \) con la topología estándar.

Este intervalo contiene todos los números reales entre 0 y 1, incluidos ambos extremos.

En este caso, el interior de \( A \) es \( (0,1) \).

$$ \text{Int}(A) = (0,1) $$

Este es el mayor intervalo abierto contenido en \( A \), que excluye los puntos 0 y 1, ya que no pueden formar parte de ningún subconjunto abierto que esté completamente dentro de \( A \).

Ejemplo 2

Ahora consideremos el conjunto \( A = [0,1) \) en \( \mathbb{R} \) con la misma topología estándar.

Este conjunto contiene todos los números reales desde 0 (incluido) hasta 1 (excluido), formando un intervalo cerrado a la izquierda y abierto a la derecha.

Sin embargo, el interior de \( A \) sigue siendo el mismo que en el caso anterior:

\[ \text{Int}(A) = (0,1) \]

Esto se debe a que el interior de un conjunto es la unión de todos los subconjuntos abiertos que están completamente contenidos en él. El mayor subconjunto abierto dentro de \( [0,1) \) es precisamente \( (0,1) \).

Nota: En \( \mathbb{R} \) con la topología estándar, los conjuntos abiertos están formados por uniones de intervalos abiertos. Por ello, el único subconjunto abierto más grande contenido en \( [0,1) \) es \( (0,1) \), ya que 0 no pertenece a ningún intervalo abierto que esté completamente dentro de \( A \).

Ejemplo 3

Ahora consideremos el conjunto \( A = [0,1) \) bajo una topología discreta en \( X \).

En un espacio con topología discreta, todos los subconjuntos son abiertos por definición.

Esto implica que cualquier punto de \( A \) tiene un entorno abierto completamente contenido en \( A \).

En la topología discreta sobre \( \mathbb{R} \), cualquier subconjunto es abierto, ya sea un intervalo, un conjunto finito de puntos o incluso combinaciones arbitrarias de elementos. Así, en \( A = [0,1) \), conjuntos como \( (0,0.5) \), \( (0.25,0.75) \), \( (0,1) \) y también \( [0,0.25] \), así como el conjunto vacío y el conjunto completo \( [0,1) \), son abiertos.

En esta topología, el propio conjunto \( A \) es un conjunto abierto.

Por lo tanto, el interior de \( A \) es simplemente \( A \) mismo:

$$ \text{Int}(A) = A = [0,1) $$

En una topología discreta, el interior de cualquier conjunto siempre coincide con el conjunto mismo.

Nota: Este ejemplo muestra cómo la elección de la topología puede cambiar la estructura de los entornos y el interior de los conjuntos. Como mencionamos antes, el interior depende de la topología del espacio \( X \) donde se encuentra \( A \), y no solo de \( A \) en sí.

Ejemplo 4

Consideremos un espacio topológico \( X \) formado por los puntos \( \{a, b, c\} \), con una topología discreta.

En este contexto, cualquier subconjunto de \( X \) es abierto:

• Por definición, \( \emptyset \) y \( \{a, b, c\} \) son abiertos en \( X \).
• Los conjuntos unitarios \( \{a\} \), \( \{b\} \) y \( \{c\} \) también son abiertos, ya que en la topología discreta cada punto es un conjunto abierto.
• Los subconjuntos con dos elementos, como \( \{a, b\} \), \( \{a, c\} \) y \( \{b, c\} \), también son abiertos.

Si consideramos el conjunto \( A = \{b, c\} \) dentro de \( X \):

Por definición, el interior de \( A \) es la unión de todos los subconjuntos abiertos contenidos en \( A \).

En este caso, los subconjuntos abiertos de \( A \) son \( \{b\} \), \( \{c\} \) y \( \{b, c\} \).

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

Por lo tanto, el interior de \( A \) coincide con \( A \).

En conclusión, \( \text{Int}(A) = A \).

Nota: Este resultado no es exclusivo de \( A \); se aplica a cualquier subconjunto \( S \subseteq X \) en una topología discreta. En este tipo de espacio, todos los subconjuntos son abiertos, por lo que \( \text{Int}(S) = S \).

Teorema del Interior de un Conjunto

En un espacio topológico \( X \), dado un subconjunto \( S \) y un elemento \( y \in X \), el punto \( y \) pertenece al interior de \( S \), denotado \( \operatorname{Int}(S) \), si y solo si existe un conjunto abierto \( U \) tal que \( y \in U \subseteq S \). En términos matemáticos, $$ y \in \text{Int}(S) \iff \exists \ U \text{ abierto, con } y \in U \subseteq S $$

En otras palabras, un punto \( y \) está en el interior de \( S \) si existe un entorno abierto \( U \) que lo contiene y que está completamente incluido en \( S \).

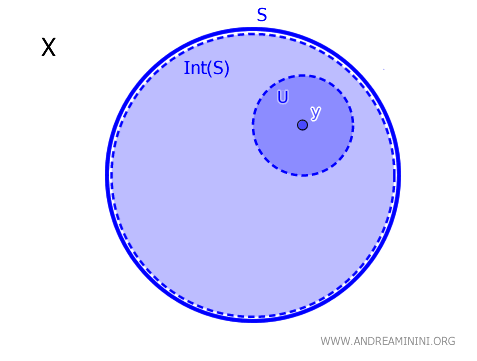
Este teorema proporciona un criterio necesario y suficiente para determinar si un punto \( y \) pertenece al interior de un conjunto \( S \) en un espacio topológico \( X \).

Demostración

• Condición necesaria: Si \( y \) pertenece al interior de \( S \), por definición, existe un conjunto abierto \( U \) en \( X \) tal que \( y \in U \) y \( U \subseteq S \). Esto confirma que si \( y \in \operatorname{Int}(S) \), entonces debe existir tal conjunto \( U \), lo que satisface la implicación “si \( y \) está en \( \operatorname{Int}(S) \), entonces existe un \( U \) abierto que lo contiene y está dentro de \( S \)”.
• Condición suficiente: Si existe un conjunto abierto \( U \) tal que \( y \in U \subseteq S \), entonces, por la propia definición del interior y la naturaleza de los conjuntos abiertos, todos los puntos de \( U \), incluido \( y \), pertenecen a \( \operatorname{Int}(S) \). Dado que el interior de un conjunto es la unión de todos los subconjuntos abiertos contenidos en él, necesariamente \( y \in \operatorname{Int}(S) \).

Nota: Este teorema es fundamental porque establece un vínculo directo entre la noción de conjunto abierto y la pertenencia al interior de un conjunto. Su aplicación es clave en el estudio de la continuidad y otras propiedades topológicas.

Ejemplo

Consideremos el conjunto \( A = [1,3] \) de números reales en el intervalo cerrado de 1 a 3 dentro del espacio topológico \( \mathbb{R} \) con la topología estándar.

$$ A = [1,3] $$

Este conjunto contiene todos los puntos comprendidos entre 1 y 3, incluyendo los extremos.

Para determinar su interior, aplicaremos el teorema del interior de un conjunto.

Determinación del Interior de \( A \)

Buscamos un conjunto abierto \( U \) tal que \( U \subseteq A \) y todos sus puntos pertenezcan a \( \operatorname{Int}(A) \).

1. Elección de \( U \)
   Tomemos \( U = (1,3) \), el intervalo abierto de 1 a 3 excluyendo los extremos. Este conjunto es abierto en la topología estándar de \( \mathbb{R} \) porque es un intervalo abierto.
2. Verificación de que \( U \subseteq A \)
   Se observa que todos los puntos de \( U = (1,3) \) pertenecen a \( A = [1,3] \), con la excepción de los extremos \( 1 \) y \( 3 \), que no están en \( U \) porque un intervalo abierto en \( \mathbb{R} \) no incluye sus extremos.

Así, \( U \) es un conjunto abierto completamente contenido en \( A \), lo que implica que todos sus puntos pertenecen al interior de \( A \). En consecuencia, el interior de \( A \), \( \operatorname{Int}(A) \), es precisamente \( (1,3) \).

Nota: Este resultado muestra que el interior de \( A \) es el intervalo abierto \( (1,3) \). Los puntos en los extremos, \( 1 \) y \( 3 \), no pertenecen a \( \operatorname{Int}(A) \) porque no existe ningún conjunto abierto contenido en \( A \) que los incluya.

Propiedades del Interior

En esta sección se analizan diversas propiedades del interior de los conjuntos en un espacio topológico. Cada una de estas propiedades revela relaciones fundamentales entre operaciones topológicas como el interior, el cierre, la unión y la intersección, algunas de las cuales pueden resultar contraintuitivas.

• Propiedad de la Unión de Interiores
  La unión de los interiores de dos conjuntos siempre está contenida en el interior de su unión. Sin embargo, esta inclusión no implica necesariamente igualdad entre ambos conjuntos. $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
• Propiedad de la Intersección de Interiores
  La intersección de los interiores de dos conjuntos coincide exactamente con el interior de su intersección. $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
• Relación entre el Interior del Complemento y el Complemento del Cierre
  El interior del complemento de un conjunto \( A \) es igual al complemento del cierre de \( A \). $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
• Relación entre el Cierre del Complemento y el Complemento del Interior
  El cierre del complemento de un conjunto \( A \) coincide con el complemento de su interior. $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

Notas

Algunas observaciones adicionales sobre las propiedades del interior.

• Si \( U \) es un conjunto abierto en \( X \) y \( U \subseteq A \), entonces \( U \subseteq \operatorname{Int}(A) \)
  Si \( U \) es un conjunto abierto en un espacio topológico \( X \) y está contenido en otro conjunto \( A \), entonces \( U \) también está contenido en el interior de \( A \). Dado que \( \operatorname{Int}(A) \) es el mayor conjunto abierto contenido en \( A \), cualquier conjunto abierto \( U \) con \( U \subseteq A \) debe necesariamente estar incluido en \( \operatorname{Int}(A) \).
• Si \( A \subseteq B \), entonces \( \operatorname{Int}(A) \subseteq \operatorname{Int}(B) \)
  Si un conjunto \( A \) está contenido en otro conjunto \( B \), entonces el interior de \( A \) también está contenido en el interior de \( B \). Esto se debe a que cualquier conjunto abierto dentro de \( A \) es también un subconjunto de \( B \). En consecuencia, la operación de tomar el interior respeta la inclusión de conjuntos.
• Un conjunto \( A \) es abierto si y solo si \( A = \operatorname{Int}(A) \)
  En un espacio topológico \( X \), un conjunto \( A \) es abierto si y solo si coincide con su interior. Es decir, \( A \) es abierto si cada uno de sus puntos posee un entorno abierto completamente contenido en \( A \). En términos formales, \( A \) es abierto si y solo si \( A = \operatorname{Int}(A) \), lo que significa que \( A \) contiene todos los conjuntos abiertos posibles que pueden estar en su interior.
• Cómo calcular el interior de un conjunto en R
  El lenguaje R es especialmente adecuado para cálculos matemáticos y estadísticos, por lo que es una herramienta ideal para este tipo de análisis. Gracias a sus funciones avanzadas, es posible calcular y visualizar de manera eficiente los interiores de conjuntos en un espacio topológico.

Y así sucesivamente.