Espacios conexos por trayectorias
Un espacio topológico S es conexo por trayectorias si existe una trayectoria continua que enlaza cualquier par de puntos A y B dentro del mismo, sin necesidad de salir de este espacio.
Imagina una hoja de papel sin tomar en cuenta sus bordes.
Este representa un área continua y se considera un espacio abierto porque excluye los límites.
En ella, entre cualquier par de puntos A y B, podrías trazar una línea con un bolígrafo sin levantarlo del papel.
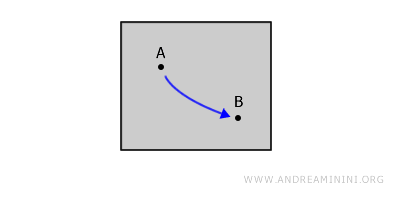
En resumen, la trayectoria no se sale del espacio que contiene a los puntos A y B.
Un espacio conexo por trayectorias es inherentemente un espacio conectado.
Esto puede parecer obvio; si un espacio estuviese desconectado, quedaría dividido en partes separadas, impidiendo que cualquier par de puntos esté conectado por una trayectoria continua sin salir del espacio.
No obstante, lo contrario no es necesariamente cierto. No todos los espacios conectados son conexos por trayectorias.
Considera este escenario, que aunque pueda parecer contraintuitivo, es completamente posible.
Tomemos, por ejemplo, dos conjuntos, Q y T:
$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$
$$ T = \{ \ 0 \} $$
El primer conjunto, Q, incluye todos los puntos a lo largo de una onda senoidal definida para todos los números reales R, excepto el cero, donde resulta indefinida por la división entre cero, una operación no definida.
El segundo conjunto, T, solo incluye el punto cero.
Los conjuntos Q y T están infinitamente próximos el uno del otro, como lo ilustra el gráfico de la función continua sin(1/x).
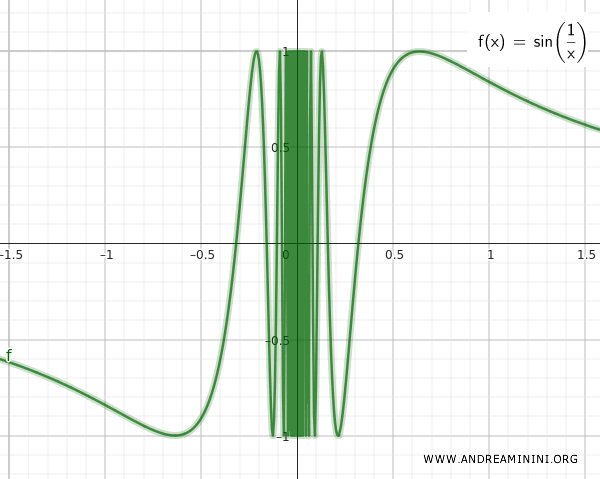
El conjunto S es la unión de Q y T.
$$ S = Q \cup T $$
El conjunto S está conectado porque, para cualquier ε>0, existe un vecindario alrededor de cero (0-ε, 0+ε) que incluye puntos de Q.
Esto se debe a que el cero es un punto de acumulación de la función sin(1/x).
Aun así, S no es conexo por trayectorias porque no existe un arco que pueda conectar cualquier punto de Q con el cero (conjunto T).
Nota: La situación sería diferente si la función fuera f(x)=1/x, porque en ese caso, es evidente que los conjuntos Q y T son disjuntos, no infinitamente cercanos.
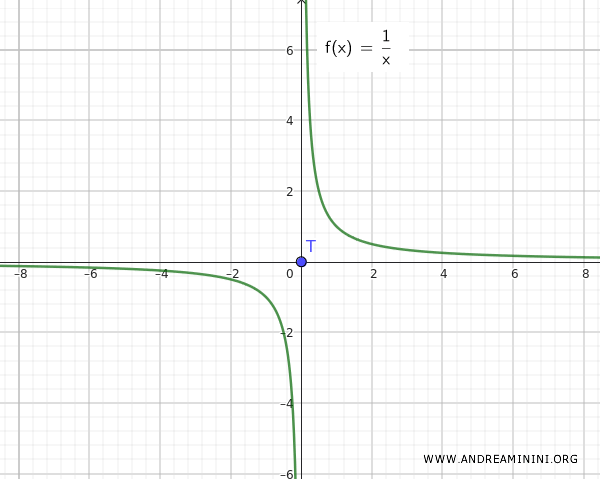
Este ejemplo demuestra que la unión de un conjunto conectado Q={∀ x ∈ R-{0}, 1/x} y un punto aislado T={0} no crea necesariamente un conjunto conectado, a menos que dicho punto aislado (por ejemplo, el cero) también sea un punto de acumulación.
Y así sucesivamente.